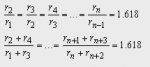История и свойства последовательности

[FXWizard]

История и свойства последовательности

Леонард Фибоначчи (XII – XIII в.н.э., Италия, Пиза) – один из величайших математиков Средневековья. В одном и своих трудов “Книга вычислений” Фибоначчи описал индо-арабскую систему исчисления и преимущества ее использования перед римской.

И почему имя великого Фибоначчи неразрывно связано с техническим анализом рынков?

Причина заключается в так называемой числовой последовательности Фибоначчи, состоящей из цифр 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144… Фибоначчи открыл ее при наблюдении потомства у семьи кроликов.

Числовая последовательность Фибоначчи имеет много интересных свойств. Например, сумма двух соседних чисел последовательности дает значение следующего за ними (например, 1+1=2; 2+3=5 и т.д.).

• Одним из самых главных следствий этих свойств является существование так называемых коэффициентов Фибоначчи, т.е. постоянных соотношений различных членов последовательности. Они определяются следующим образом: Отношение каждого числа к последующему более и более стремится к 0.618 по увеличении порядкового номера. Отношение же каждого числа к предыдущему стремится к 1.618 (обратному к 0.618). Число 0.618 называют j (фи), и мы поговорим о нем подробнее немного позже;
• При делении каждого числа на следующее за ним через одно получаем число 0.382; наоборот – соответственно 2.618;
• Подбирая таким образом соотношения, получаем основной набор коэффициентов Фибоначчи: … 4.235, 2.618, 1.618, 0.618, 0.382, 0.236. упомянем также 0.5 (1/2). Все они играют особую роль в природе, и в частности – в техническом анализе.

Важно отметить, что Фибоначчи как бы напомнил свою последовательность человечеству. Она была известна еще древним грекам и египтянам. И действительно, с тех пор в природе, архитектуре, изобразительном искусстве, математике, физике, астрономии, биологии и многих других областях были найдены закономерности, описываемые коэффициентами Фибоначчи.

Например, число 0.618 представляет собой постоянный коэффициент в так называемом золотом сечении (рис.1), где любой отрезок делится таким образом, что соотношение между его меньшей и большей частью равно соотношению между большей частью и всем отрезком. Таким образом, число 0.618 известно еще как золотой коэффициент или золотая середина. Такого типа пропорцию можно встретить практически везде (рис.2).

 

[FXWizard]

Золотой коэффициент используется природой для построения ее частей, начиная от больших и заканчивая малыми. Современная наука считает, что Вселенная развивается по так называемой золотой спирали (рис.3), которая строится именно с помощью золотого коэффициента. Эта спираль в буквальном смысле не имеет конца и начала. Меньшие витки никогда не сходятся в одну и ту же точку, а большие неограниченно развиваются в пространстве.

 

[FXWizard]

Некоторые из соблюдающихся соотношений:

 

[FXWizard]

важное заключается в том, что с помощью всех этих, в каком-то роде мистических, чисел, описываются разнородные процессы во Вселенной. Опустимся на землю и выскажем смелую мысль – почему бы не использовать Последовательность Фибоначчи при прогнозировании цены, т.е. в техническом анализе?

Эта мысль действительно смелая. Ее высказал еще в 30-е годы один из самых известных людей, внесших вклад в теорию технического анализа – Ральф Нельсон Эллиотт. С тех пор конкретная польза применения этой идеи практически во всех методах технического анализа не вызывает сомнения.


Определение отрезков времени и использование чисел Фибоначчи при установлении длительности циклов


Один из простейших способов применения чисел Фибоначчи на практике – определение отрезков времени, через которое произойдет то или иное событие, например, изменение тренда. Аналитик отсчитывает определенное количество дней Фибоначчи или недель (13 21, 34, 55 и т.д.) от предыдущего сходного события.
Числа Фибоначчи имеют широкое применение при определении длительности периода в Теории Циклов. За основу каждого доминантного цикла берется определенное количество дней, недель, месяцев, связанное с числами Фибоначчи. Например, длина Цикла (Волны) Кондратьева равна 54 годам. Отметим близость этой величины к числу Фибоначчи 55.