FXWizard
Гуру форума
О тестировании торговых систем, оптимизации и "безопасной" торговле
Непременным атрибутом большинства современных трейдеров является комплекс программных средств, помогающих в проведении необходимых расчетов и принятии торговых решений. Современное развитие информационных и компьютерных систем делает доступным даже для неподготовленных пользователей большой спектр методов для анализа данных и статистического моделирования. Это и пакеты стастического и эконометрического анализа, эмуляторы нейронных сетей и генетических алгоритмов, программы для кластеризации и прямого анализа данных. Но большую часть прикладного программного обеспечения для системных трейдеров составляют средства для непосредственной разработки, тестирования и оптимизации торговых стратегий.
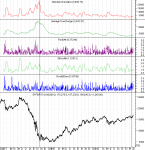
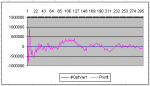
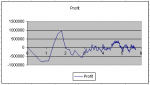
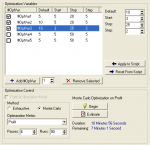
Редко у кого вызывает сомнение факт, что любую торговую систему необходимо протестировать на исторических данных. Ведь результаты объективных тестов сразу скажут, пригодна ли та или иная система для реальной торговли. Гораздо больше споров в трейдерском сообществе вызывает идея оптимизации торговых систем для улучшения ожидаемых результатов от торговли. Кто-то считает, что история никогда не повторится и оптимизировать параметры по прошлым котировкам просто бессмысленно. Другие, наоборот, оценивают статистическую значимость результатов исключительно по историческим данным. Трудно однозначно сказать, кто прав в этой ситуации. В той или иной мере любая системная торговля предполагает использование исторических закономерностей. Даже выбор той или иной стратегии уже есть оптимизация, ведь мы его делаем, опираясь на результаты прошлых оценок и тестов.
Противники оптимизации часто приводят аргумент, что выбор наилучших в прошлом параметров излишне подгоняет систему под конкретный отрезок истории. И в будущем такая система будет крайне неустойчива. Так обязательно и случится, если просто выбрать комбинацию параметров, дающую наибольшую прибыль на конкретном отрезке времени. Но к оптимизации этот выбор не будет иметь никакого отношения, а будет являть собой классическую подгонку. Теория оптимизации - это сложная наука, со своими правилами, теоремами и аксиомами. По оптимизации торговых систем написано несколько работ, позволяющих провести четкую грань между грамотным выбором робастных параметров и глупой подгонкой под историю. В этой статье я хочу рассказать о нескольких интересных моментах, связанных с тестированием, оптимизацией и оценкой устойчивости торговых алгоритмов.
Непременным атрибутом большинства современных трейдеров является комплекс программных средств, помогающих в проведении необходимых расчетов и принятии торговых решений. Современное развитие информационных и компьютерных систем делает доступным даже для неподготовленных пользователей большой спектр методов для анализа данных и статистического моделирования. Это и пакеты стастического и эконометрического анализа, эмуляторы нейронных сетей и генетических алгоритмов, программы для кластеризации и прямого анализа данных. Но большую часть прикладного программного обеспечения для системных трейдеров составляют средства для непосредственной разработки, тестирования и оптимизации торговых стратегий.
Редко у кого вызывает сомнение факт, что любую торговую систему необходимо протестировать на исторических данных. Ведь результаты объективных тестов сразу скажут, пригодна ли та или иная система для реальной торговли. Гораздо больше споров в трейдерском сообществе вызывает идея оптимизации торговых систем для улучшения ожидаемых результатов от торговли. Кто-то считает, что история никогда не повторится и оптимизировать параметры по прошлым котировкам просто бессмысленно. Другие, наоборот, оценивают статистическую значимость результатов исключительно по историческим данным. Трудно однозначно сказать, кто прав в этой ситуации. В той или иной мере любая системная торговля предполагает использование исторических закономерностей. Даже выбор той или иной стратегии уже есть оптимизация, ведь мы его делаем, опираясь на результаты прошлых оценок и тестов.
Противники оптимизации часто приводят аргумент, что выбор наилучших в прошлом параметров излишне подгоняет систему под конкретный отрезок истории. И в будущем такая система будет крайне неустойчива. Так обязательно и случится, если просто выбрать комбинацию параметров, дающую наибольшую прибыль на конкретном отрезке времени. Но к оптимизации этот выбор не будет иметь никакого отношения, а будет являть собой классическую подгонку. Теория оптимизации - это сложная наука, со своими правилами, теоремами и аксиомами. По оптимизации торговых систем написано несколько работ, позволяющих провести четкую грань между грамотным выбором робастных параметров и глупой подгонкой под историю. В этой статье я хочу рассказать о нескольких интересных моментах, связанных с тестированием, оптимизацией и оценкой устойчивости торговых алгоритмов.