FXWizard
Гуру форума
Оконченная пьеса для механической системы
Разработку механической торговой системы мы начали четыре года назад по двум направлениям. Первый путь базировался на корреляционной теории случайных процессов и оказался тупиковым. Второй основывался на идее одного из авторов настоящей статьи и ранее хорошо зарекомендовал себя при анализе геофизических, медико-биологических и экономических процессов, поэтому мы почти не сомневались в успехе...
Мы шли к ней четыре года...
Потребовались четыре годa упорных поисков и многомесячные тестирования промежуточных версий, прежде чем были получены результаты, достойные внимания. Разработка первой механической торговой системы (МТС «MAGUS») шла совместно с компанией TruSoft.
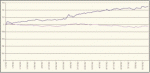
Для иллюстрации эффективности последней версии на рисунке 1 показана норма прибыли, полученная за 2002 г. по механической системе (красная линия) и по индексу S&P 500 (зеленая линия). Данные за другие годы (1999-2001), для сравнения, приведены в таблице 1.

Рис. 1. Норма прибыли, полученная за 2002 год по механической системе (красная линия) и по индексу S&P 500 (зеленая линия). Ежедневно покупаются акции всего списка компаний, полученного системой.

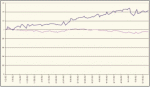
При расчете нормы прибыли учтены комиссионные затраты ($20 за покупку/продажу пакета и $0.05 за покупку каждой акции) и ограничения на объем покупаемого пакета – не более 3% от числа проданных акций в предыдущий день и на сумму V.$25,000. Распределение ежедневно необходимого капитала имеет резко выраженную правостороннюю асимметрию, т.е. значение Mx (табл. 1) необходимо иметь в течение нескольких дней. Прибыль в процентах к V получена в расчете на одну сделку. Норма прибыли на рисунке 1 получена при условии, что реализуются все покупки, предлагаемые системой (в отдельные дни количество их может быть больше 10). На рисунке 2 показана норма прибыли за 5 месяцев 2002 года для наиболее неблагоприятного случая, когда каждый день покупаются акции только одной компании, произвольно выбранной из ежедневных списков, по которым получены результаты на рисунке 1.

Рис. 2. Норма прибыли, полученная за 2002 год по механической системе (красная линия) и по индексу S&P 500 (зеленая линия). Ежедневно покупаются акции одной компании, случайно выбранной из всего списка, полученного системой.
Случайный отбор повторялся 5 раз, на рисунке 2 приведен наихудший случай. Несмотря на то, что результаты за этот год оказались самыми плохими за последние четыре года (табл. 2), однако даже в этом случае наша МТС существенно «переигрывает» рынок.

Нам кажется, что полученные результаты являются неординарными, поэтому мы решили познакомить трейдеров и финансистов с нашей системой. На каких принципах строится МТС.
Таких основных принципов четыре.
Принцип 1. Рынок рассматривается как открытая сложная неоднородная система, в которой всегда наблюдаются колебания параметров состояния разных временных масштабов L0,L1,L2,...,Ln. Колебания масштаба Li+1 обусловлены изменением параметров колебаний масштаба Li. Если условия на внешней границе системы Li+1 резко изменяются в случайные моменты времени tj или закономерно во времени, но на случайную величину .yj, то изменения внутренних характеристик системы Li+1 (и свойств подсистем Li) будут представлять случайный процесс. Важно отличать изменения, обусловленные нелинейным характером процесса, от случайного процесса. В первом случае изменения могут быть очень быстрыми, но все же состояние системы можно предсказать в момент времени tj+1, если известны ее состояния до момента tj. Во втором случае предсказание невозможно в принципе.
Принцип 2. Для описания и предсказания рынка необходимо использовать рекуррентный способ описания [1]. Это означает, что для описания системы Li+1 достаточно знать свойства подсистем Li. Модель системы с более высоким иерархическим уровнем может быть, и часто оказывается, более простой по сравнению с моделью системы более низкого уровня.
Принцип 3. Для описания поведения рынка, начиная с некоторого уровня, достаточно использовать эмпирические методы, приемы и критерии, применяемые при моделировании простых систем, т.е. методы теории эксперимента, теории ошибок, теории регрессионного анализа и статистического оценивания.
Принцип 4. Предпосылки математических методов не должны противоречить природе объекта, для исследования которого используются данные методы. Предпосылками математического метода называют условия (ограничения, требования), при которых получен данный метод (например, для применения метода наименьших квадратов необходимо, чтобы дискретность независимых переменных была существенно больше погрешности их измерения). Под природой объекта в данном случае понимается совокупность свойств эмпирических данных, отображающих поведение объекта в пространстве и во времени. Простейшим свойством эмпирических данных является, к примеру, корреляционная зависимость их между собой во времени. Условия применения методов, особенно статистических, обычно не очевидны, и во многих случаях для их определения требуется проведение специальных исследований. Правильное применение известных математических методов для анализа экономических процессов представляет проблему. В 70-е годы прошлого века этот вопрос очень интенсивно разрабатывался в эконометрии, опубликовано огромное число работ. Анализ проблемы привел к единодушному выводу: чем больше несоответствие между предпосылками математического метода и свойствами объекта исследования, тем меньше шансов, что данный метод в данной задаче может привести к позитивному результату.
Нетрудно заметить, что сформулированные принципы полностью укладываются в методологию системного подхода. Системный подход не является аппаратом или методом построения моделей – это методология научного исследования, которая может быть применена к любому объекту и в любой ситуации [2].
Основополагающие положения системного подхода давно разработаны и хорошо изложены в литературе [2]. Нашу методику следует рассматривать лишь как дальнейшее развитие системного подхода. Сущность развития состоит в том, что для анализа рынка ценных бумаг мы применили некоторые принципы системного анализа процессов в естественных науках.
Почему системный анализ используется неэффективно?
Изложенные принципы являются необходимыми и достаточными для построения механической торговой системы. Особенно важным является четвертый принцип. Несмотря на то, что он достаточно хорошо известен осведомленным читателям, в практической работе, как правило, игнорируется.
Приведем несколько характерных примеров.
Пример 1. Известно, что эмпирические значения, отображающие процесс любого временного масштаба, не являются абсолютно точными. Любая эмпирическая характеристика всегда измеряется (определяется) с некоторой погрешностью. Более того, вообще о наличии процесса можно говорить лишь в том случае, если изменения заданного временного масштаба превышают погрешность измерения этих колебаний. Иначе говоря, нельзя приступать к анализу до тех пор, пока не получена оценка погрешности исследуемых переменных. К сожалению, примеров такого отношения к данным при решении задач трейдера мы не встречали.
Пример 2. При решении задач трейдера также не ставится вопрос о соотношении масштаба колебаний и дискретности измерений. Можно показать, что если дискретность получения эмпирических значений того же порядка, что и период колебаний, то не может быть никакой надежды получить прибыль от разности цен при покупке и продаже, даже в том случае, если мы своевременно определили начало и окончание фазы роста цены.
Пример 3. Рассмотрим пример некритического отношения к математическому методу, применение которого в лучшем случае может быть бесполезным, а в худшем – опасным для финансовых операций. В работе Ч. Миллера [3] приведена убедительная аргументация в пользу предсказуемости поведения рынка с помощью математических методов. Иначе говоря, «самое ближайшее будущее» функционально связано с прошлым, но при условии, что за период «между прошлым и будущим» на систему не было влияния случайных факторов. В противном случае прогнозирование, по существу, становится бессмысленным до тех пор, пока мы не уйдем достаточно далеко от точки воздействия случайного фактора и не сможем оценить новую закономерную связь. Иначе говоря, мы имеем возможность прогнозировать, но каждый раз стоим перед необходимостью учитывать, что в любой момент времени состояние системы может измениться на случайную величину.
Наша методика: откуда берется эффективность
Итак, при разработке МТС мы учитывали, что:
При разработке системы были приняты следующие допущения.
1. Наилучшие условия для покупки акций наблюдаются в момент времени, когда значения волновых процессов всех временных масштабов достигают локальных минимумов, а для продажи – в момент времени, когда значения волновых процессов всех масштабов, меньших заданной позиции, одновременно достигают наибольших значений.
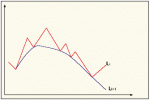
2. Эмпирические значения волнового процесса масштаба Li+1 совпадают со значениями фазовой точки колебаний масштаба Li (рис. 3). Эмпирическими значениями короткопериодных колебаний являются значения цены при открытии и закрытии.

Рис. 3. Условный временной ряд для иллюстрации связи колебаний разных периодов.
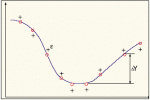
3. Минимум волнового процесса находится путем сравнения разности сглаженных значений delta-Y с размахом погрешности Re (рис. 4).

Рис. 4. Определение погрешности и оценки фазового состояния волнового процесса в точке t0.
4. В решении задачи трейдера используются следующие периоды колебаний цен акций:
Здесь, как и в техническом анализе, периодом волны считается промежуток времени между двумя смежными экстремумами. Это удобно потому, что обычно быков интересует лишь фаза возрастания, а медведей – фаза убывания волны, в общепринятом ее понимании.
5. Определение колебаний разных временных масштабов осуществляется последовательно, начиная с наименьшего масштаба. Алгоритм и методы анализа движения рынка непосредственно связаны с изложенными выше допущениями. Определяющим здесь, очевидно, является метод определения колебаний разных временных масштабов. От эффективности решения этого вопроса зависит эффективность решения всей задачи.
Анализ методов скользящегo среднего и методов фильтрации с помощью цифровых фильтров показал, что применение их является совершенно бесперспективным, т.к. они эффективны лишь в том случае, когда период и амплитуда искомого колебания почти не меняются во времени. Поэтому для данной цели был разработан оригинальный численный эвристический метод, который мы назвали «метод мягкого сглаживания». Этот же метод используется и для оценки погрешностей эмпирических значений всех волновых процессов.
Особенность метода состоит в том, что он слабо искажает естественную и не генерирует ложную закономерную составляющую. Эффективность метода не зависит от условий стационарности параметров волнового процесса. Чем меньше дискретность измерений, тем выше эффективность метода. Сглаживание последовательности случайных чисел с постоянным средним порождает ряд с коэффициентом автокорреляции примерно 0.15 (т.е. почти случайный ряд) и дисперсией в 3 раза меньше дисперсии исходного ряда. Следовательно, процедуру сглаживания можно повторить, после чего получим ряд с незначительными колебаниями около нуля.
Для сравнения: при одноразовом сглаживании случайного ряда скользящим средним по трем точкам мы получим ряд с такой же дисперсией, но с коэффициентом автокорреляции 0.65, т.е. он будет содержать ложный волновой процесс. К чему это может привести на практике, едва ли следует пояснять. Для оценки состояния волновых процессов (среднепериодных, длиннопериодных и волн Эллиотта), а также для получения линий сопротивления и поддержки используются регрессионные модели, содержащие небольшое число гармонических функций. Модели находятся известным методом включения переменных при условии статистически значимого уменьшения остаточной дисперсии. Определение периодов гармоник осуществляется по аналогии со спектральным методом, но не совпадает с ним. Гармонические функции используются для определения начального приближения состояния процесса.
Оказывается, что в следующем приближении почти всегда более эффективной является либо модель, включающая небольшое число эмпирических, в общем случае – не ортогональных функций, либо конечно-разностный аналог нелинейного дифференциального уравнения невысокого порядка. Эти модели являются особенно эффективными для оценки состояния длиннопериодных колебаний.
Помощник трейдера
Мы называем свою систему «Помощник трейдера». Ее можно использовать в трех режимах – механическом (в этом случае трейдер выполняет лишь функции статиста), полумеханическом (трейдер работает по строго заданному алгоритму) и автономном (трейдер использует систему лишь как инструмент для принятия решения).
Предполагаем, что доработка методических основ нашей механической торговой системы позволит улучшить результат в несколько раз, т.е. добиться получения 300-400% годовых. И это – лишь малая часть (порядка 10%) от той прибыли, которую можно было бы получить с помощью механической системы «задним числом», т.е. имея будущие значения цены. Хотя едва ли уровень реальных доходов можно поднять существенно выше 300-400% – помехой этому является значительная погрешность эмпирических значений волновых процессов, уменьшить которую невозможно никакими современными методиками обработки. Поэтому нам не грозит перспектива получения беспроигрышной торговой системы, которая очень скоро изжила бы сама себя. Очевидно, что хорошая механическая система на данном рынке может работать лишь в единственном экземпляре. Если же режим работы ручной или полумеханический, то наиболее вероятно, что решения, принимаемые разными трейдерами, почти не будут пересекаться, если количество трейдеров, использующих данную систему, не превышает число Nt=Px/P, где Px – потенциально доступная прибыль (ее можно принять равной 3000%), P – максимальная прибыль данной системы в механическом режиме.
Наша торговая система позволяет работать в широком диапазоне свободного капитала – от $100 тыс. до $10 млн. Система обеспечивает стабильную прибыль (не менее 50% годовых) даже при самой неблагоприятной ситуации, когда портфель содержит акции одного наименования. Наконец, пожалуй, самое главное состоит в том, что изложенный системный подход в полной мере можно использовать для решения долгосрочных инвестиционных задач и вообще для широкого круга экономических задач, включая оценку макроэкономического состояния страны, региона или мира. Эффективность решения такого рода задач проверена на примере анализа доходов и расходов в России в начале 90-х годов.
По материалам сайта www.spekulant.ru
Разработку механической торговой системы мы начали четыре года назад по двум направлениям. Первый путь базировался на корреляционной теории случайных процессов и оказался тупиковым. Второй основывался на идее одного из авторов настоящей статьи и ранее хорошо зарекомендовал себя при анализе геофизических, медико-биологических и экономических процессов, поэтому мы почти не сомневались в успехе...
Мы шли к ней четыре года...
Потребовались четыре годa упорных поисков и многомесячные тестирования промежуточных версий, прежде чем были получены результаты, достойные внимания. Разработка первой механической торговой системы (МТС «MAGUS») шла совместно с компанией TruSoft.
Для иллюстрации эффективности последней версии на рисунке 1 показана норма прибыли, полученная за 2002 г. по механической системе (красная линия) и по индексу S&P 500 (зеленая линия). Данные за другие годы (1999-2001), для сравнения, приведены в таблице 1.
Рис. 1. Норма прибыли, полученная за 2002 год по механической системе (красная линия) и по индексу S&P 500 (зеленая линия). Ежедневно покупаются акции всего списка компаний, полученного системой.
При расчете нормы прибыли учтены комиссионные затраты ($20 за покупку/продажу пакета и $0.05 за покупку каждой акции) и ограничения на объем покупаемого пакета – не более 3% от числа проданных акций в предыдущий день и на сумму V.$25,000. Распределение ежедневно необходимого капитала имеет резко выраженную правостороннюю асимметрию, т.е. значение Mx (табл. 1) необходимо иметь в течение нескольких дней. Прибыль в процентах к V получена в расчете на одну сделку. Норма прибыли на рисунке 1 получена при условии, что реализуются все покупки, предлагаемые системой (в отдельные дни количество их может быть больше 10). На рисунке 2 показана норма прибыли за 5 месяцев 2002 года для наиболее неблагоприятного случая, когда каждый день покупаются акции только одной компании, произвольно выбранной из ежедневных списков, по которым получены результаты на рисунке 1.
Рис. 2. Норма прибыли, полученная за 2002 год по механической системе (красная линия) и по индексу S&P 500 (зеленая линия). Ежедневно покупаются акции одной компании, случайно выбранной из всего списка, полученного системой.
Случайный отбор повторялся 5 раз, на рисунке 2 приведен наихудший случай. Несмотря на то, что результаты за этот год оказались самыми плохими за последние четыре года (табл. 2), однако даже в этом случае наша МТС существенно «переигрывает» рынок.
Нам кажется, что полученные результаты являются неординарными, поэтому мы решили познакомить трейдеров и финансистов с нашей системой. На каких принципах строится МТС.
Таких основных принципов четыре.
Принцип 1. Рынок рассматривается как открытая сложная неоднородная система, в которой всегда наблюдаются колебания параметров состояния разных временных масштабов L0,L1,L2,...,Ln. Колебания масштаба Li+1 обусловлены изменением параметров колебаний масштаба Li. Если условия на внешней границе системы Li+1 резко изменяются в случайные моменты времени tj или закономерно во времени, но на случайную величину .yj, то изменения внутренних характеристик системы Li+1 (и свойств подсистем Li) будут представлять случайный процесс. Важно отличать изменения, обусловленные нелинейным характером процесса, от случайного процесса. В первом случае изменения могут быть очень быстрыми, но все же состояние системы можно предсказать в момент времени tj+1, если известны ее состояния до момента tj. Во втором случае предсказание невозможно в принципе.
Принцип 2. Для описания и предсказания рынка необходимо использовать рекуррентный способ описания [1]. Это означает, что для описания системы Li+1 достаточно знать свойства подсистем Li. Модель системы с более высоким иерархическим уровнем может быть, и часто оказывается, более простой по сравнению с моделью системы более низкого уровня.
Принцип 3. Для описания поведения рынка, начиная с некоторого уровня, достаточно использовать эмпирические методы, приемы и критерии, применяемые при моделировании простых систем, т.е. методы теории эксперимента, теории ошибок, теории регрессионного анализа и статистического оценивания.
Принцип 4. Предпосылки математических методов не должны противоречить природе объекта, для исследования которого используются данные методы. Предпосылками математического метода называют условия (ограничения, требования), при которых получен данный метод (например, для применения метода наименьших квадратов необходимо, чтобы дискретность независимых переменных была существенно больше погрешности их измерения). Под природой объекта в данном случае понимается совокупность свойств эмпирических данных, отображающих поведение объекта в пространстве и во времени. Простейшим свойством эмпирических данных является, к примеру, корреляционная зависимость их между собой во времени. Условия применения методов, особенно статистических, обычно не очевидны, и во многих случаях для их определения требуется проведение специальных исследований. Правильное применение известных математических методов для анализа экономических процессов представляет проблему. В 70-е годы прошлого века этот вопрос очень интенсивно разрабатывался в эконометрии, опубликовано огромное число работ. Анализ проблемы привел к единодушному выводу: чем больше несоответствие между предпосылками математического метода и свойствами объекта исследования, тем меньше шансов, что данный метод в данной задаче может привести к позитивному результату.
Нетрудно заметить, что сформулированные принципы полностью укладываются в методологию системного подхода. Системный подход не является аппаратом или методом построения моделей – это методология научного исследования, которая может быть применена к любому объекту и в любой ситуации [2].
Основополагающие положения системного подхода давно разработаны и хорошо изложены в литературе [2]. Нашу методику следует рассматривать лишь как дальнейшее развитие системного подхода. Сущность развития состоит в том, что для анализа рынка ценных бумаг мы применили некоторые принципы системного анализа процессов в естественных науках.
Почему системный анализ используется неэффективно?
Изложенные принципы являются необходимыми и достаточными для построения механической торговой системы. Особенно важным является четвертый принцип. Несмотря на то, что он достаточно хорошо известен осведомленным читателям, в практической работе, как правило, игнорируется.
Приведем несколько характерных примеров.
Пример 1. Известно, что эмпирические значения, отображающие процесс любого временного масштаба, не являются абсолютно точными. Любая эмпирическая характеристика всегда измеряется (определяется) с некоторой погрешностью. Более того, вообще о наличии процесса можно говорить лишь в том случае, если изменения заданного временного масштаба превышают погрешность измерения этих колебаний. Иначе говоря, нельзя приступать к анализу до тех пор, пока не получена оценка погрешности исследуемых переменных. К сожалению, примеров такого отношения к данным при решении задач трейдера мы не встречали.
Пример 2. При решении задач трейдера также не ставится вопрос о соотношении масштаба колебаний и дискретности измерений. Можно показать, что если дискретность получения эмпирических значений того же порядка, что и период колебаний, то не может быть никакой надежды получить прибыль от разности цен при покупке и продаже, даже в том случае, если мы своевременно определили начало и окончание фазы роста цены.
Пример 3. Рассмотрим пример некритического отношения к математическому методу, применение которого в лучшем случае может быть бесполезным, а в худшем – опасным для финансовых операций. В работе Ч. Миллера [3] приведена убедительная аргументация в пользу предсказуемости поведения рынка с помощью математических методов. Иначе говоря, «самое ближайшее будущее» функционально связано с прошлым, но при условии, что за период «между прошлым и будущим» на систему не было влияния случайных факторов. В противном случае прогнозирование, по существу, становится бессмысленным до тех пор, пока мы не уйдем достаточно далеко от точки воздействия случайного фактора и не сможем оценить новую закономерную связь. Иначе говоря, мы имеем возможность прогнозировать, но каждый раз стоим перед необходимостью учитывать, что в любой момент времени состояние системы может измениться на случайную величину.
Наша методика: откуда берется эффективность
Итак, при разработке МТС мы учитывали, что:
- временные ряды, с которыми имеет дело трейдер, есть композиция колебаний разных временных масштабов с нерегулярными периодами, амплитудами и фазами;
- эмпирические значения, характеризующие колебания данного временного масштаба, содержат погрешности измерений, которыми нельзя пренебрегать;
- соотношение между дискретностью получения эмпирических значений и периодом колебаний может быть неблагоприятным для использования данного колебания в задачах трейдера, и это соотношение должно быть определено заранее;
- современная теория случайных процессов не позволяет выявлять во временном ряду последовательность случайных событий, поэтому для решения данного вопроса необходимо разрабатывать специальные методы.
При разработке системы были приняты следующие допущения.
1. Наилучшие условия для покупки акций наблюдаются в момент времени, когда значения волновых процессов всех временных масштабов достигают локальных минимумов, а для продажи – в момент времени, когда значения волновых процессов всех масштабов, меньших заданной позиции, одновременно достигают наибольших значений.
2. Эмпирические значения волнового процесса масштаба Li+1 совпадают со значениями фазовой точки колебаний масштаба Li (рис. 3). Эмпирическими значениями короткопериодных колебаний являются значения цены при открытии и закрытии.
Рис. 3. Условный временной ряд для иллюстрации связи колебаний разных периодов.
3. Минимум волнового процесса находится путем сравнения разности сглаженных значений delta-Y с размахом погрешности Re (рис. 4).
Рис. 4. Определение погрешности и оценки фазового состояния волнового процесса в точке t0.
4. В решении задачи трейдера используются следующие периоды колебаний цен акций:
- 1-3 часа – ультракороткие позиции (внутридневные колебания);
- от 1 до 5 дней – короткие позиции;
- от 5 до 25 дней – среднесрочные позиции;
- несколько месяцев – длинные позиции.
Здесь, как и в техническом анализе, периодом волны считается промежуток времени между двумя смежными экстремумами. Это удобно потому, что обычно быков интересует лишь фаза возрастания, а медведей – фаза убывания волны, в общепринятом ее понимании.
5. Определение колебаний разных временных масштабов осуществляется последовательно, начиная с наименьшего масштаба. Алгоритм и методы анализа движения рынка непосредственно связаны с изложенными выше допущениями. Определяющим здесь, очевидно, является метод определения колебаний разных временных масштабов. От эффективности решения этого вопроса зависит эффективность решения всей задачи.
Анализ методов скользящегo среднего и методов фильтрации с помощью цифровых фильтров показал, что применение их является совершенно бесперспективным, т.к. они эффективны лишь в том случае, когда период и амплитуда искомого колебания почти не меняются во времени. Поэтому для данной цели был разработан оригинальный численный эвристический метод, который мы назвали «метод мягкого сглаживания». Этот же метод используется и для оценки погрешностей эмпирических значений всех волновых процессов.
Особенность метода состоит в том, что он слабо искажает естественную и не генерирует ложную закономерную составляющую. Эффективность метода не зависит от условий стационарности параметров волнового процесса. Чем меньше дискретность измерений, тем выше эффективность метода. Сглаживание последовательности случайных чисел с постоянным средним порождает ряд с коэффициентом автокорреляции примерно 0.15 (т.е. почти случайный ряд) и дисперсией в 3 раза меньше дисперсии исходного ряда. Следовательно, процедуру сглаживания можно повторить, после чего получим ряд с незначительными колебаниями около нуля.
Для сравнения: при одноразовом сглаживании случайного ряда скользящим средним по трем точкам мы получим ряд с такой же дисперсией, но с коэффициентом автокорреляции 0.65, т.е. он будет содержать ложный волновой процесс. К чему это может привести на практике, едва ли следует пояснять. Для оценки состояния волновых процессов (среднепериодных, длиннопериодных и волн Эллиотта), а также для получения линий сопротивления и поддержки используются регрессионные модели, содержащие небольшое число гармонических функций. Модели находятся известным методом включения переменных при условии статистически значимого уменьшения остаточной дисперсии. Определение периодов гармоник осуществляется по аналогии со спектральным методом, но не совпадает с ним. Гармонические функции используются для определения начального приближения состояния процесса.
Оказывается, что в следующем приближении почти всегда более эффективной является либо модель, включающая небольшое число эмпирических, в общем случае – не ортогональных функций, либо конечно-разностный аналог нелинейного дифференциального уравнения невысокого порядка. Эти модели являются особенно эффективными для оценки состояния длиннопериодных колебаний.
Помощник трейдера
Мы называем свою систему «Помощник трейдера». Ее можно использовать в трех режимах – механическом (в этом случае трейдер выполняет лишь функции статиста), полумеханическом (трейдер работает по строго заданному алгоритму) и автономном (трейдер использует систему лишь как инструмент для принятия решения).
Предполагаем, что доработка методических основ нашей механической торговой системы позволит улучшить результат в несколько раз, т.е. добиться получения 300-400% годовых. И это – лишь малая часть (порядка 10%) от той прибыли, которую можно было бы получить с помощью механической системы «задним числом», т.е. имея будущие значения цены. Хотя едва ли уровень реальных доходов можно поднять существенно выше 300-400% – помехой этому является значительная погрешность эмпирических значений волновых процессов, уменьшить которую невозможно никакими современными методиками обработки. Поэтому нам не грозит перспектива получения беспроигрышной торговой системы, которая очень скоро изжила бы сама себя. Очевидно, что хорошая механическая система на данном рынке может работать лишь в единственном экземпляре. Если же режим работы ручной или полумеханический, то наиболее вероятно, что решения, принимаемые разными трейдерами, почти не будут пересекаться, если количество трейдеров, использующих данную систему, не превышает число Nt=Px/P, где Px – потенциально доступная прибыль (ее можно принять равной 3000%), P – максимальная прибыль данной системы в механическом режиме.
Наша торговая система позволяет работать в широком диапазоне свободного капитала – от $100 тыс. до $10 млн. Система обеспечивает стабильную прибыль (не менее 50% годовых) даже при самой неблагоприятной ситуации, когда портфель содержит акции одного наименования. Наконец, пожалуй, самое главное состоит в том, что изложенный системный подход в полной мере можно использовать для решения долгосрочных инвестиционных задач и вообще для широкого круга экономических задач, включая оценку макроэкономического состояния страны, региона или мира. Эффективность решения такого рода задач проверена на примере анализа доходов и расходов в России в начале 90-х годов.
По материалам сайта www.spekulant.ru