FXWizard
Гуру форума
Парадоксы сложных процентов
В статье рассматриваются некоторые довольно неожиданные качественные эффекты, связанные с начислением процентов на проценты.
О логике и математике
Существуют разные взгляды на соотношение логики и математики. Некоторые серьезные мыслители рассматривают математику как часть логики. Существует и прямо противоположная точка зрения, согласно которой логика является частью математики. Логика – это система принципов, позволяющих делать верныe выводы на основе правильных посылок. Эти принципы были сформулированы еще Аристотелем и с тех пор не претерпели существенных изменений. Удивление может вызвать тот факт, что эти простые правила за столь длительное время не привели ни к одной ошибке.
Одно из возможных объяснений этому состоит в том, что в них сконцентрирован опыт, накопленный человечеством на протяжении многих десятков тысяч лет. Примерно сто лет назад один из математиков писал: «С чувством непреодолимого отвращения я отшатываюсь от достойного всякого сожаления зла – непрерывных функций, не имеющих производных». Интуиция подсказывала большинству математиков того времени, что таких функций не должно существовать. А упрямая логика твердила, что почти все функции именно такие гадкие. К счастью, возобладала логика, иначе было бы невозможно создание атомных электростанций, персональных компьютеров и мобильных телефонов. Рассмотренное противоречие дало начало систематическим попыткам найти пробелы в логической системе. Такие попытки продолжались на протяжении всего ХХ века, но к успеху не привели. Логика оказалась непогрешимой.
Об экспоненциальном росте
После такого вступления уже можно рассмотреть логические и математические парадоксы, связанные с экспоненциальным ростом при начислении процентов на проценты.
Возьмем обычный газетный лист. Сложим его вдвое, потом еще вдвое и так далее. Попробуйте быстро оценить, какую толщину будет иметь газета, если мы проделаем эту операцию 50 раз? А теперь давайте посчитаем. После одной операции мы будем иметь два слоя бумаги, после двух – 4, после трех – 8..., после пятидесяти – 250. Если толщина газетного листа равна 0.1 миллиметра, то толщина пачки будет равна:
250/10=(210)5/10=10245/10>10005/10= =(105)3/10=1015/10=1014 миллиметров, или сто миллионов километров. Для сравнения: расстояние от Земли до Солнца равно примерно 150 миллионам километров.
Какое все это имеет отношение к финансовым рынкам? Да самое прямое! Мне несколько раз попадались компьютерные программы, авторы которых утверждали, что с их помощью можно на рынке FOREX зарабатывать порядка тысячи процентов годовых. Это значит, что капитал инвестора, пользующегося этой программой, каждый год увеличивается примерно в десять раз. Начав со скромной суммы в тысяч, инвестор уже через два года станет миллионером, через пять – миллиардером, а еще лет через пять приберет к рукам все деньги на Земле. Остается непонятным, почему авторы программ сами не применят их на практике, а продают их за довольно скромные деньги? Из приведенных рассуждений видно, что доходность в тысячу процентов годовых слишком велика, и нельзя рассчитывать на стабильное получение такого дохода в течение достаточно долгого времени. Кстати, рассмотренный выше пример с газетой соответствует доходности в 100% годовых. Из приведенных оценок следует, что если речь идет о работе на рынке в течение 50 лет, то получить доходность в 100% годовых в принципе невозможно. Таким образом, если мы говорим о финансовых операциях с реинвестицией полученной прибыли, то с оценками доходности нужно быть достаточно осторожными.
Кое-какие характерные величины собраны в таблице 1. В ее первом столбце приведена дневная доходность, во втором та же доходность переведена в годовую, а в третьем она же пересчитана на срок в 50 лет. Из таблицы, в частности, видно, что для срока в 50 лет даже доходность 0.1% в день является запредельной!

Рассмотренные выше примеры говорят об одном: модели экспоненциального роста имеют весьма ограниченную область применимости. Например, газету еще никому не удавалось сложить вдвое десять раз. Физики хорошо знают, что экспонента – это модель взрыва. Еще один классический пример того, как в моделях экспоненциального роста не учитываются границы их применимости, дает теория Мальтуса.
Гарантированные выигрыши
Хорошо известен следующий способ получить гарантированный выигрыш при игре в орлянку. Поставим на кон 1 рубль. Если в первой же игре мы выиграем, то игру сразу же прекратим. В противном случае удвоим ставку и сыграем еще раз. В случае выигрыша прекратим игру, а иначе вновь удвоим ставку – и так далее. Вероятность проиграть в первой игре равна 0.5. Вероятность проиграть два раза подряд равна 1/4, три раза подряд – 1/8, вероятность проиграть n раз подряд равна 2-n. Видим, что эта вероятность экспоненциально быстро убывает, поэтому с вероятностью единица игра закончится на каком-то шаге. Подсчитаем прибыли и убытки в случае, если это произошло в игре с номером n.
В первой игре мы проиграли рубль, во второй – два, в (n-1)-ной 2n-2 рублей, а в последней – выиграли 2n-1 рублей. Итог всей операции – один рубль выигрыша*. Результат явно парадоксальный. Корень парадокса заключается в экспоненциальном росте размера ставок. Разобранный выше пример с газетой свидетельствует о том, что уже на пятидесятую ставку никаких денег не хватит. У реального игрока проблемы начнутся гораздо раньше.
Описанный эффект имеет чисто качественный характер и относится отнюдь не только к игре орел-решка.
Допустим, мы работаем на финансовом рынке и имеем какой-то инструмент, выдающий сигналы на вход в рынок. Установим стоп-ордера так, чтобы в случае удачи получать f рублей на вложенный рубль, а в случае неудачи фиксировать убыток в g рублей на вложенный рубль. Можно предположить, что результат такой операции – случайное событие, и с вероятностью p мы получим прибыль, а с вероятностью q=1-p зафиксируем убыток.
Допустим, мы хотим заработать сумму M (миллион). Откроем первую позицию в размере M/f. Если операция закончится с прибылью, то задача решена. В противном случае продолжим игру, вложив сумму M(1+g)/f и так далее. Вероятность проиграть n раз подряд, очевидно, равна qn и быстро стремится к нулю с ростом n. Поэтому с вероятностью единица мы рано или поздно выиграем и заработаем свой миллион.
Все сказанное носит чисто качественный характер: результат не зависит ни от наших амбиций, ни от размеров прибыли и убытка, ни даже от вероятности выигрыша. Важно лишь, чтобы вероятность выигрыша была ненулевой. Правда, и размер инвестируемых средств будет экспоненциально расти независимо от всех этих параметров. Поэтому и объяснение парадокса имеет чисто качественный характер.
Петербургский парадокс
Еще один парадокс такого рода был предложен в 1713 году Николаем Бернулли. По месту публикации он носит название петербургского парадокса. Рассмотрим следующую ситуацию. Петр и Павел уговариваются сыграть ряд партий в орла или решку. Если Петр выигрывает первую партию, Павел платит ему 2 рубля, и игра прекращается. Если Петр проигрывает первую партию и выигрывает вторую, Павел выплачивает ему 4 рубля, и игра заканчивается... Если Петр проигрывает подряд n-1 партий, а затем выигрывает n-ную, Павел выплачивает ему 2n рублей, и игра прекращается. Спрашивается, какова справедливая плата за участие в такой игре? Вероятность получить выигрыш в размере 2n, очевидно, равна 1/2n. События эти независимы, поэтому математическое ожидание выигрыша Петра равно: 2(1/2)+4(1/4)+...+2n(1/2n)+... = = 1+1+..., то есть равно бесконечности.
Таким образом, сколько бы ни заплатил Петр в начале игры, в конце концов он, вероятно, окажется в выигрыше. А между тем никакой здравомыслящий человек на месте Петра не согласился бы поставить и ста рублей против обязательств Павла.
Этот парадокс достаточно долго занимал математиков. Была даже разработана альтернативная теории вероятностей теория морального ожидания. А ларчик открывался просто. Объяснение было дано, насколько я понимаю, Эмилем Борелем [1] в первой половине прошлого века.
Объяснение парадокса опять связано с экспоненциальным ростом ставок. Давайте представим, что Павел продает свои обязательства по частям. Плата в один рубль за право с вероятностью 1/2 получить два рубля и с вероятностью 1/2 не получить ничего – вполне справедлива, и, вероятно, Павел найдет покупателя. То же относится и к обязательству выплатить 4 рубля с вероятностью 1/4 и ничего не платить с вероятностью 3/4. А вот продать за рубль право получить 250 рублей или не получить ничего – Павлу вряд ли удастся, ибо каждый нормальный человек сообразит, что таких денег у Павла нет.
Если учесть это обстоятельство, можно сказать, что справедливая плата за участие в игре никак не больше 50 рублей. Кстати, этот пример можно перевести на язык опционов, поэтому он не так уж далек от реальной жизни. А выводы, как и в предыдущем примере, носят качественный характер.
Разобранные примеры показывают, что если в математической модели явно или неявно появляется экспоненциальный рост, то нужно очень внимательно отслеживать границы применимости модели.
Реинвестиции прибыли
Пусть имеются два способа вложения денег. При способе А мы будем каждый год стабильно получать прибыль в f рублей на вложенный изначально рубль. При способе Б мы будем получать в год прибыль в g рублей на вложенный рубль, но с возможностью многократной реинвестиции полученной прибыли. Какой способ предпочесть?
Давайте посчитаем. Каждый вложенный рубль при способе Б через n лет превратится в сумму (1+g)n. Прибыль за n-ный год при этом составит:
(1+g)n-(1+g)n-1=g(1+g)n-1.
Видно, что получаемая прибыль год от года растет, причем скорость роста прибыли g(1+g)n-1-g(1+g)n-2=g2(1+g)n-2 не меньше g2. Поэтому не позднее, чем через T=2f/g2 лет прибыль при способе Б будет вдвое превышать прибыль, получаемую при способе А. Значит уже через 2T лет суммарная прибыль от вложений при способе Б превысит суммарную прибыль от вложений способом А**. Таким образом, если у нас в запасе достаточно много времени, то способ Б определенно предпочтительнее. И это – независимо от соотношения ставок f и g! Кстати, этот вывод останется верным и в том случае, когда периодичности получения прибыли при этих двух способах не совпадают. Более того, он не зависит и от частоты получения прибыли, лишь бы эта частота при способе Б была положительной.
Напрашивается вывод о том, что способ Б лучше. Но, с другой стороны, если мы вкладываем деньги всего на год, а f>g, то при способе А мы заработаем больше. Поэтому правильный вывод выглядит следующим образом. Если f>g, то все зависит от срока инвестиций: если он меньше некоторого порогового значения – предпочтительнее способ А, а в противном случае – способ Б.
Некоторые авторы, рекламируя свой способ управления объемом инвестиций, совершенно упускают это обстоятельство из виду. Так, один автор [2] советует: «Рассматривайте каждую игру как бесконечно повторяющуюся». А между тем срок инвестиций определяется конкретными жизненными обстоятельствами инвестора, а не рекомендациями специалистов, пусть даже и очень авторитетных. Более того, многие инвесторы не склонны заглядывать слишком далеко в будущее, и в современной российской действительности такая точка зрения часто оказывается оправданной. Кстати, слегка видоизменяя некоторые рассуждения, можно показать, что если достаточно долго играть в игру с ненулевой вероятностью убытков, то с вероятностью единица разоришься. Над этим тоже стоит задуматься, прежде чем рассматривать игру как бесконечно повторяющуюся. Описанная модель не учитывает еще одного обстоятельства – необходимости «затрат на жизнь». Пусть каждый год инвестор должен тратить некую сумму m на аренду помещения, зарплату сотрудникам и т.п. Тогда при способе А динамика счета инвестора будет определяться равенством xt+1=xt+x0 f-m, а при способе Б – равенством yt+1=(1+g)yt-m.
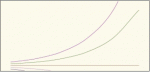
Здесь xt и yt – остаток на счете в году t в первом и во втором случаях, а x0=y0 – начальная сумма инвестиций. Первая формула задает хорошо знакомую со школы геометрическую прогрессию, поэтому сразу можно сказать, что xt=x0+(x0 f-m)(t-1). Со второй нужно немножко повозиться. Если мы инвестируем сумму m/g, то полученной прибыли в конце года как раз хватит на необходимые выплаты. Если есть возможность инвестировать больше, то условно разделим всю сумму на две части: первая в размере m/g будет использоваться для поддержания деятельности, а остаток будет реинвестироваться вместе с прибылью. Поэтому yt=m/g+(y0-m/g)(1+g)t-1. В последней формуле мы видим все ту же экспоненту, поэтому можем сделать вывод, что при достаточно большой начальной сумме и при достаточно большом сроке инвестиций способ Б лучше, независимо от ставок f и g. Но появляется и новый качественный эффект (рис. 1).

Динамика счета при различных начальных условиях.
При некоторых соотношениях между объемом начального капитала, размером необходимых затрат и доходностью операций может случиться так, что способ А дает возможность сколь угодно долго жить безбедно, а способ Б неизбежно приводит к разорению***. Заметим, кстати, что если есть возможность комбинировать эти два способа, то при больших сроках инвестиции оптимальным становится портфель, соответствующий вложению суммы m/f по способу А и остальных денег – по способу Б (несложные выкладки оставляем читателю).
Отметим еще одно забавное обстоятельство. Сравним найденную выше функцию yt с геометрической прогрессией zt=y0(1+h)t-1. Рассуждения, аналогичные приведенным выше, показывают, что если hzt, а при h>g справедливо обратное неравенство. Отсюда следует, что «эффективная доходность» вложений по способу Б равна g независимо от размера расходов m, если только начальная сумма достаточно велика! По аналогичным соображениям, эффективная доходность вложений по способу А независимо ни от чего равна нулю! Выводы несколько парадоксальные, и связаны они с тем, что мы рассматриваем очень большие сроки инвестиций.
Фактор времени
До сих пор мы использовали в основном один факт. А именно, несложно понять, что график любой экспоненты может быть получен из графика любой другой экспоненты просто изменением масштаба времени. В примере с газетой для того, чтобы перейти от функции 2t к функции 10t мы изменили масштаб времени в 10/3 раза. Поэтому, имея в виду лишь очень большие периоды времени, можно было говорить о любой из этих экспонент, например, о той, которая описывает складывание газеты вдвое. Правда, понятие «очень большие периоды времени» существенно зависит от конкретной экспоненты (и в меньшей – от нужной нам степени точности).
Теперь обсудим другое обстоятельство, которое, по-видимому, во многом определяет неадекватное восприятие всего, что связано со сложными процентами. Как и всякая гладкая функция, экспонента хорошо аппроксимируется прямой. Это означает, в частности, что при очень маленьких периодах времени прибыль, вычисленная по формуле простого процента, практически не отличается от прибыли, вычисленной по формуле сложныx процентов. Понятие «очень маленький период времени» опять-таки существенно зависит от конкретной экспоненты.
На практике часто приходится сталкиваться с экспоненциальными зависимостями, у которых основание экспоненты достаточно близко к единице. А в таком случае представляющие практический интерес периоды времени могут оказаться «очень маленькими». И тогда решения, принятые на основе линейного приближения, окажутся верными.
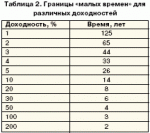
Некоторое представление об этом дает таблица 2. В ней для различных значений доходности приведено время, спустя которое прибыль по формуле простого процента будет вдвое меньше прибыли, посчитанной по формуле сложных процентов. Многие еще помнят те времена, когда в сберегательных кассах начисляли 2% годовых. Из таблицы видно, что в этом случае 50 лет – «маленький период времени».

Попутно заметим еще одно обстоятельство. На многих рынках размер торгуемого лота достаточно велик. Можно показать, что на доходность в отдаленной перспективе это не влияет. А вот понятия «маленький период времени» и «большой период времени» могут существенно измениться в сторону увеличения соответствующих границ. Итак, обращаясь к какой-то инвестиционной задаче, мы должны прежде всего решить, что нас интересует: ближайшее будущее или отдаленная перспектива. Впрочем, может оказаться, что ни то ни другое предположение нас не устраивает. Это, пожалуй, самый худший вариант, поскольку, как показывает опыт, крайние случаи обычно исследуются легче.
В качестве примера коснемся вкратце вопроса об управлении размером открытой позиции в условиях риска. В [2] рассмотрен вариант очень больших периодов времени и выяснено, что разумнее всего входить в рынок, используя лишь часть имеющихся средств. С другой стороны, нетрудно понять, что если плановый горизонт очень близок, то в таком случае достаточную точность обеспечит линейное приближение, и принцип «деньги должны работать» станет верным, то есть правильно будет использовать все имеющиеся средства. Вопрос о том, когда можно пользоваться тем и другим приближением, и что делать в «промежуточном» случае – заслуживает отдельного обсуждения.
Сноски:
* Как это следует из знакомой со школы формулы суммы членов геометрической прогрессии.
** Здесь нас интересует лишь качественный эффект, поэтому я ограничиваюсь весьма грубыми оценками. При желании в этой задаче такие оценки легко могут быть уточнены.
*** Можно было бы учесть и издержки, пропорциональные обороту (комиссионные, налоги на прибыль и т. п.). Однако к новым качественным эффектам это не приводит, поскольку легко сводится просто к уменьшению ставок f и g.
Михаил Горелов www.spekulant.ru
В статье рассматриваются некоторые довольно неожиданные качественные эффекты, связанные с начислением процентов на проценты.
О логике и математике
Существуют разные взгляды на соотношение логики и математики. Некоторые серьезные мыслители рассматривают математику как часть логики. Существует и прямо противоположная точка зрения, согласно которой логика является частью математики. Логика – это система принципов, позволяющих делать верныe выводы на основе правильных посылок. Эти принципы были сформулированы еще Аристотелем и с тех пор не претерпели существенных изменений. Удивление может вызвать тот факт, что эти простые правила за столь длительное время не привели ни к одной ошибке.
Одно из возможных объяснений этому состоит в том, что в них сконцентрирован опыт, накопленный человечеством на протяжении многих десятков тысяч лет. Примерно сто лет назад один из математиков писал: «С чувством непреодолимого отвращения я отшатываюсь от достойного всякого сожаления зла – непрерывных функций, не имеющих производных». Интуиция подсказывала большинству математиков того времени, что таких функций не должно существовать. А упрямая логика твердила, что почти все функции именно такие гадкие. К счастью, возобладала логика, иначе было бы невозможно создание атомных электростанций, персональных компьютеров и мобильных телефонов. Рассмотренное противоречие дало начало систематическим попыткам найти пробелы в логической системе. Такие попытки продолжались на протяжении всего ХХ века, но к успеху не привели. Логика оказалась непогрешимой.
Об экспоненциальном росте
После такого вступления уже можно рассмотреть логические и математические парадоксы, связанные с экспоненциальным ростом при начислении процентов на проценты.
Возьмем обычный газетный лист. Сложим его вдвое, потом еще вдвое и так далее. Попробуйте быстро оценить, какую толщину будет иметь газета, если мы проделаем эту операцию 50 раз? А теперь давайте посчитаем. После одной операции мы будем иметь два слоя бумаги, после двух – 4, после трех – 8..., после пятидесяти – 250. Если толщина газетного листа равна 0.1 миллиметра, то толщина пачки будет равна:
250/10=(210)5/10=10245/10>10005/10= =(105)3/10=1015/10=1014 миллиметров, или сто миллионов километров. Для сравнения: расстояние от Земли до Солнца равно примерно 150 миллионам километров.
Какое все это имеет отношение к финансовым рынкам? Да самое прямое! Мне несколько раз попадались компьютерные программы, авторы которых утверждали, что с их помощью можно на рынке FOREX зарабатывать порядка тысячи процентов годовых. Это значит, что капитал инвестора, пользующегося этой программой, каждый год увеличивается примерно в десять раз. Начав со скромной суммы в тысяч, инвестор уже через два года станет миллионером, через пять – миллиардером, а еще лет через пять приберет к рукам все деньги на Земле. Остается непонятным, почему авторы программ сами не применят их на практике, а продают их за довольно скромные деньги? Из приведенных рассуждений видно, что доходность в тысячу процентов годовых слишком велика, и нельзя рассчитывать на стабильное получение такого дохода в течение достаточно долгого времени. Кстати, рассмотренный выше пример с газетой соответствует доходности в 100% годовых. Из приведенных оценок следует, что если речь идет о работе на рынке в течение 50 лет, то получить доходность в 100% годовых в принципе невозможно. Таким образом, если мы говорим о финансовых операциях с реинвестицией полученной прибыли, то с оценками доходности нужно быть достаточно осторожными.
Кое-какие характерные величины собраны в таблице 1. В ее первом столбце приведена дневная доходность, во втором та же доходность переведена в годовую, а в третьем она же пересчитана на срок в 50 лет. Из таблицы, в частности, видно, что для срока в 50 лет даже доходность 0.1% в день является запредельной!
Рассмотренные выше примеры говорят об одном: модели экспоненциального роста имеют весьма ограниченную область применимости. Например, газету еще никому не удавалось сложить вдвое десять раз. Физики хорошо знают, что экспонента – это модель взрыва. Еще один классический пример того, как в моделях экспоненциального роста не учитываются границы их применимости, дает теория Мальтуса.
Гарантированные выигрыши
Хорошо известен следующий способ получить гарантированный выигрыш при игре в орлянку. Поставим на кон 1 рубль. Если в первой же игре мы выиграем, то игру сразу же прекратим. В противном случае удвоим ставку и сыграем еще раз. В случае выигрыша прекратим игру, а иначе вновь удвоим ставку – и так далее. Вероятность проиграть в первой игре равна 0.5. Вероятность проиграть два раза подряд равна 1/4, три раза подряд – 1/8, вероятность проиграть n раз подряд равна 2-n. Видим, что эта вероятность экспоненциально быстро убывает, поэтому с вероятностью единица игра закончится на каком-то шаге. Подсчитаем прибыли и убытки в случае, если это произошло в игре с номером n.
В первой игре мы проиграли рубль, во второй – два, в (n-1)-ной 2n-2 рублей, а в последней – выиграли 2n-1 рублей. Итог всей операции – один рубль выигрыша*. Результат явно парадоксальный. Корень парадокса заключается в экспоненциальном росте размера ставок. Разобранный выше пример с газетой свидетельствует о том, что уже на пятидесятую ставку никаких денег не хватит. У реального игрока проблемы начнутся гораздо раньше.
Описанный эффект имеет чисто качественный характер и относится отнюдь не только к игре орел-решка.
Допустим, мы работаем на финансовом рынке и имеем какой-то инструмент, выдающий сигналы на вход в рынок. Установим стоп-ордера так, чтобы в случае удачи получать f рублей на вложенный рубль, а в случае неудачи фиксировать убыток в g рублей на вложенный рубль. Можно предположить, что результат такой операции – случайное событие, и с вероятностью p мы получим прибыль, а с вероятностью q=1-p зафиксируем убыток.
Допустим, мы хотим заработать сумму M (миллион). Откроем первую позицию в размере M/f. Если операция закончится с прибылью, то задача решена. В противном случае продолжим игру, вложив сумму M(1+g)/f и так далее. Вероятность проиграть n раз подряд, очевидно, равна qn и быстро стремится к нулю с ростом n. Поэтому с вероятностью единица мы рано или поздно выиграем и заработаем свой миллион.
Все сказанное носит чисто качественный характер: результат не зависит ни от наших амбиций, ни от размеров прибыли и убытка, ни даже от вероятности выигрыша. Важно лишь, чтобы вероятность выигрыша была ненулевой. Правда, и размер инвестируемых средств будет экспоненциально расти независимо от всех этих параметров. Поэтому и объяснение парадокса имеет чисто качественный характер.
Петербургский парадокс
Еще один парадокс такого рода был предложен в 1713 году Николаем Бернулли. По месту публикации он носит название петербургского парадокса. Рассмотрим следующую ситуацию. Петр и Павел уговариваются сыграть ряд партий в орла или решку. Если Петр выигрывает первую партию, Павел платит ему 2 рубля, и игра прекращается. Если Петр проигрывает первую партию и выигрывает вторую, Павел выплачивает ему 4 рубля, и игра заканчивается... Если Петр проигрывает подряд n-1 партий, а затем выигрывает n-ную, Павел выплачивает ему 2n рублей, и игра прекращается. Спрашивается, какова справедливая плата за участие в такой игре? Вероятность получить выигрыш в размере 2n, очевидно, равна 1/2n. События эти независимы, поэтому математическое ожидание выигрыша Петра равно: 2(1/2)+4(1/4)+...+2n(1/2n)+... = = 1+1+..., то есть равно бесконечности.
Таким образом, сколько бы ни заплатил Петр в начале игры, в конце концов он, вероятно, окажется в выигрыше. А между тем никакой здравомыслящий человек на месте Петра не согласился бы поставить и ста рублей против обязательств Павла.
Этот парадокс достаточно долго занимал математиков. Была даже разработана альтернативная теории вероятностей теория морального ожидания. А ларчик открывался просто. Объяснение было дано, насколько я понимаю, Эмилем Борелем [1] в первой половине прошлого века.
Объяснение парадокса опять связано с экспоненциальным ростом ставок. Давайте представим, что Павел продает свои обязательства по частям. Плата в один рубль за право с вероятностью 1/2 получить два рубля и с вероятностью 1/2 не получить ничего – вполне справедлива, и, вероятно, Павел найдет покупателя. То же относится и к обязательству выплатить 4 рубля с вероятностью 1/4 и ничего не платить с вероятностью 3/4. А вот продать за рубль право получить 250 рублей или не получить ничего – Павлу вряд ли удастся, ибо каждый нормальный человек сообразит, что таких денег у Павла нет.
Если учесть это обстоятельство, можно сказать, что справедливая плата за участие в игре никак не больше 50 рублей. Кстати, этот пример можно перевести на язык опционов, поэтому он не так уж далек от реальной жизни. А выводы, как и в предыдущем примере, носят качественный характер.
Разобранные примеры показывают, что если в математической модели явно или неявно появляется экспоненциальный рост, то нужно очень внимательно отслеживать границы применимости модели.
Реинвестиции прибыли
Пусть имеются два способа вложения денег. При способе А мы будем каждый год стабильно получать прибыль в f рублей на вложенный изначально рубль. При способе Б мы будем получать в год прибыль в g рублей на вложенный рубль, но с возможностью многократной реинвестиции полученной прибыли. Какой способ предпочесть?
Давайте посчитаем. Каждый вложенный рубль при способе Б через n лет превратится в сумму (1+g)n. Прибыль за n-ный год при этом составит:
(1+g)n-(1+g)n-1=g(1+g)n-1.
Видно, что получаемая прибыль год от года растет, причем скорость роста прибыли g(1+g)n-1-g(1+g)n-2=g2(1+g)n-2 не меньше g2. Поэтому не позднее, чем через T=2f/g2 лет прибыль при способе Б будет вдвое превышать прибыль, получаемую при способе А. Значит уже через 2T лет суммарная прибыль от вложений при способе Б превысит суммарную прибыль от вложений способом А**. Таким образом, если у нас в запасе достаточно много времени, то способ Б определенно предпочтительнее. И это – независимо от соотношения ставок f и g! Кстати, этот вывод останется верным и в том случае, когда периодичности получения прибыли при этих двух способах не совпадают. Более того, он не зависит и от частоты получения прибыли, лишь бы эта частота при способе Б была положительной.
Напрашивается вывод о том, что способ Б лучше. Но, с другой стороны, если мы вкладываем деньги всего на год, а f>g, то при способе А мы заработаем больше. Поэтому правильный вывод выглядит следующим образом. Если f>g, то все зависит от срока инвестиций: если он меньше некоторого порогового значения – предпочтительнее способ А, а в противном случае – способ Б.
Некоторые авторы, рекламируя свой способ управления объемом инвестиций, совершенно упускают это обстоятельство из виду. Так, один автор [2] советует: «Рассматривайте каждую игру как бесконечно повторяющуюся». А между тем срок инвестиций определяется конкретными жизненными обстоятельствами инвестора, а не рекомендациями специалистов, пусть даже и очень авторитетных. Более того, многие инвесторы не склонны заглядывать слишком далеко в будущее, и в современной российской действительности такая точка зрения часто оказывается оправданной. Кстати, слегка видоизменяя некоторые рассуждения, можно показать, что если достаточно долго играть в игру с ненулевой вероятностью убытков, то с вероятностью единица разоришься. Над этим тоже стоит задуматься, прежде чем рассматривать игру как бесконечно повторяющуюся. Описанная модель не учитывает еще одного обстоятельства – необходимости «затрат на жизнь». Пусть каждый год инвестор должен тратить некую сумму m на аренду помещения, зарплату сотрудникам и т.п. Тогда при способе А динамика счета инвестора будет определяться равенством xt+1=xt+x0 f-m, а при способе Б – равенством yt+1=(1+g)yt-m.
Здесь xt и yt – остаток на счете в году t в первом и во втором случаях, а x0=y0 – начальная сумма инвестиций. Первая формула задает хорошо знакомую со школы геометрическую прогрессию, поэтому сразу можно сказать, что xt=x0+(x0 f-m)(t-1). Со второй нужно немножко повозиться. Если мы инвестируем сумму m/g, то полученной прибыли в конце года как раз хватит на необходимые выплаты. Если есть возможность инвестировать больше, то условно разделим всю сумму на две части: первая в размере m/g будет использоваться для поддержания деятельности, а остаток будет реинвестироваться вместе с прибылью. Поэтому yt=m/g+(y0-m/g)(1+g)t-1. В последней формуле мы видим все ту же экспоненту, поэтому можем сделать вывод, что при достаточно большой начальной сумме и при достаточно большом сроке инвестиций способ Б лучше, независимо от ставок f и g. Но появляется и новый качественный эффект (рис. 1).
Динамика счета при различных начальных условиях.
При некоторых соотношениях между объемом начального капитала, размером необходимых затрат и доходностью операций может случиться так, что способ А дает возможность сколь угодно долго жить безбедно, а способ Б неизбежно приводит к разорению***. Заметим, кстати, что если есть возможность комбинировать эти два способа, то при больших сроках инвестиции оптимальным становится портфель, соответствующий вложению суммы m/f по способу А и остальных денег – по способу Б (несложные выкладки оставляем читателю).
Отметим еще одно забавное обстоятельство. Сравним найденную выше функцию yt с геометрической прогрессией zt=y0(1+h)t-1. Рассуждения, аналогичные приведенным выше, показывают, что если hzt, а при h>g справедливо обратное неравенство. Отсюда следует, что «эффективная доходность» вложений по способу Б равна g независимо от размера расходов m, если только начальная сумма достаточно велика! По аналогичным соображениям, эффективная доходность вложений по способу А независимо ни от чего равна нулю! Выводы несколько парадоксальные, и связаны они с тем, что мы рассматриваем очень большие сроки инвестиций.
Фактор времени
До сих пор мы использовали в основном один факт. А именно, несложно понять, что график любой экспоненты может быть получен из графика любой другой экспоненты просто изменением масштаба времени. В примере с газетой для того, чтобы перейти от функции 2t к функции 10t мы изменили масштаб времени в 10/3 раза. Поэтому, имея в виду лишь очень большие периоды времени, можно было говорить о любой из этих экспонент, например, о той, которая описывает складывание газеты вдвое. Правда, понятие «очень большие периоды времени» существенно зависит от конкретной экспоненты (и в меньшей – от нужной нам степени точности).
Теперь обсудим другое обстоятельство, которое, по-видимому, во многом определяет неадекватное восприятие всего, что связано со сложными процентами. Как и всякая гладкая функция, экспонента хорошо аппроксимируется прямой. Это означает, в частности, что при очень маленьких периодах времени прибыль, вычисленная по формуле простого процента, практически не отличается от прибыли, вычисленной по формуле сложныx процентов. Понятие «очень маленький период времени» опять-таки существенно зависит от конкретной экспоненты.
На практике часто приходится сталкиваться с экспоненциальными зависимостями, у которых основание экспоненты достаточно близко к единице. А в таком случае представляющие практический интерес периоды времени могут оказаться «очень маленькими». И тогда решения, принятые на основе линейного приближения, окажутся верными.
Некоторое представление об этом дает таблица 2. В ней для различных значений доходности приведено время, спустя которое прибыль по формуле простого процента будет вдвое меньше прибыли, посчитанной по формуле сложных процентов. Многие еще помнят те времена, когда в сберегательных кассах начисляли 2% годовых. Из таблицы видно, что в этом случае 50 лет – «маленький период времени».
Попутно заметим еще одно обстоятельство. На многих рынках размер торгуемого лота достаточно велик. Можно показать, что на доходность в отдаленной перспективе это не влияет. А вот понятия «маленький период времени» и «большой период времени» могут существенно измениться в сторону увеличения соответствующих границ. Итак, обращаясь к какой-то инвестиционной задаче, мы должны прежде всего решить, что нас интересует: ближайшее будущее или отдаленная перспектива. Впрочем, может оказаться, что ни то ни другое предположение нас не устраивает. Это, пожалуй, самый худший вариант, поскольку, как показывает опыт, крайние случаи обычно исследуются легче.
В качестве примера коснемся вкратце вопроса об управлении размером открытой позиции в условиях риска. В [2] рассмотрен вариант очень больших периодов времени и выяснено, что разумнее всего входить в рынок, используя лишь часть имеющихся средств. С другой стороны, нетрудно понять, что если плановый горизонт очень близок, то в таком случае достаточную точность обеспечит линейное приближение, и принцип «деньги должны работать» станет верным, то есть правильно будет использовать все имеющиеся средства. Вопрос о том, когда можно пользоваться тем и другим приближением, и что делать в «промежуточном» случае – заслуживает отдельного обсуждения.
Сноски:
* Как это следует из знакомой со школы формулы суммы членов геометрической прогрессии.
** Здесь нас интересует лишь качественный эффект, поэтому я ограничиваюсь весьма грубыми оценками. При желании в этой задаче такие оценки легко могут быть уточнены.
*** Можно было бы учесть и издержки, пропорциональные обороту (комиссионные, налоги на прибыль и т. п.). Однако к новым качественным эффектам это не приводит, поскольку легко сводится просто к уменьшению ставок f и g.
Михаил Горелов www.spekulant.ru