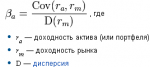FXWizard
Гуру форума
Практика парного трейдинга. Часть 1. Регрессия.
В прошлых статьях, посвященных парному трейдингу и статистическому арбитражу, я подробно рассматривал этапы подготовки и поиска акций для торговли. В общем виде торговля спредом сводится к выделению стационарного ряда из двух или более коинтегрированных инструментов. Такой подход позволяет трейдеру зарабатывать на краткосрочном дисбалансе в доходности или ценах на похожие активы. На пару аналогичных компаний из одного сектора экономики оказывают воздействие одни и те же внешние факторы. А, значит, и реагировать на такие события цены акций должны примерно одинаково. Поэтому краткосрочный дисбаланс в устоявшемся соотношении цен должен быть компенсирован в сторону долгосрочного паритета. Проще говоря, если без видимой причины одна акция показывает резкий рост относительно второй, то можно ожидать его коррекции или догоняющего роста второй акции. Именно фраза "можно ожидать" отличает статистический парный трейдинг от гарантированного математического арбитража. В таком случае временный дисбаланс, скорее всего, будет ликвидирован, но вовсе не обязательно. Мне пришло несколько похожих писем с просьбой объяснить различия между статистическим и математическим арбитражем, и корреляцией и коинтеграцией, поэтому с них и начну.
Математический арбитраж возможен только между инструментами, которые связаны между собой однозначной математической формулой. Например, цена фьючерса вполне конкретно определяется через три переменные: цену акции, безрисковую ставку и срок жизни контракта. Поэтому краткосрочные изменения в цене базовой акции должны моментально отражаться на цене фьючерса. Именно "должны" и никак иначе. В момент экспирации цены акции и фьючерса должны сойтись в одной точке просто по определению фьючерса. Поэтому любое отклонение цены фьючерса от строгого математического закона обязательно будет компенсировано. Можно провести аналогию с двумя автобусами, которые одновременно выезжают из точки А и должны одновременно приехать в точку Б. Они уже выехали - это факт, должны приехать одновременно - для обоих водителей это закон. И если один автобус в дороге задержится и отстанет, то тогда будут возможны три варианта развития событий:
- отстающий водитель увеличивает скорость и догоняет коллегу;
- опережающий водитель притормаживает и ждет;
- отстающий немного ускоряется, а опережающий немного сбавляет скорость и позволяет себя догнать.
Как видим, оба водителя могут манипулировать только скоростью своего автобуса. Но не известно, какой из этих трех вариантов они выберут. Поэтому для получения прибыли трейдеру необходимо "купить скорость" отстающего и одновременно "продать скорость" опережающего. Тогда любой из трех вариантов окажется выигрышным, ведь автобусы обязательно начнут сближение.
Чтобы объяснить суть статистического арбитража и разницу между корреляцией и коинтеграцией, приведу другую аналогию. Представим себе двух братьев, которые бегут на озеро и держат в руках достаточно длинную и упругую пружину. Один конец которой находится у первого, другой - у второго брата. Они оба бегут в одном направлении - это высокая корреляция. А то, что пружина не даст им заметно удалиться друг от друга - это коинтеграция. Какие бы зигзаги они не совершали, какой бы берег они не выбрали, их динамика движения и расстояние между ними будет определяться исключительно упругостью пружины. В этом случае вектор их перемещения примерно одинаков, но расстояние между ними на протяжении всего пути может заметно разниться. В среднем оно равно как раз длине пружины. И чем сильнее они растягивают или сжимают пружину, тем более вероятно, что она вернется к своему исходному состоянию. В этом случае переменным фактором является степень натяжения и длина пружины. Прибыль делается за счет "продажи слишком растянутой пружины" или "покупки слишком сжатой". Ставка делается на то, что рано или поздно длина пружины вернется в исходное состояние. Но проблема в том, что мы заранее не знаем ни предела натяжения пружины ни ее обычной длины, и растягивается она порой легче, чем можно себе представить. Поэтому трейдер не может сказать, что вот здесь и сейчас "степень натяжения" уже чрезмерна. Можно лишь оценить вероятность возврата к средним значениям на основании статистического анализа исторических данных. И открывая позицию, трейдер не может быть на 100% уверен в прибыли.
Частным случаем статистического арбитража является торговля парой "фьючерс РТС против портфеля фьючерсов на акции", который я рассматривал в прошлый раз. Портфель фьючерсов составлялся таким образом, чтобы его стоимостное выражение равнялось цене индексного контракта. Таким образом, получалась ситуация, когда более "тяжелый" фРТС перекрывался более "легкими" фьючерсами на акции. И часто при подобном выборе торговой пары прибыль образовывалась за счет одной-двух акций, выбившихся из общей динамики. Если в классическом арбитраже или парном трейдинге обе стороны сделки равноправны и их движения равновероятны, то тут иногда проявляется некоторая определенность. То есть можно с большей уверенностью говорить, за счет какой стороны или акции будет компенсирован ценовой дисбаланс. Чтобы это пояснить, приведу третью аналогию. Представим себе человека, который гуляет по парку, ведя на поводках трех собак разного размера. В основном, траекторию движения этой четверки определяет хозяин, а собаки образуют вокруг него броуновское движение. Его масса заметно больше и свое направление он изменит только в том случае, если все три собаки вместе потянут в одну сторону. Если же только одна из них куда-то тянет, то в скором времени ей придется подчиниться и вернуться в общий строй. Так и на бирже, только "весовое" различие между фРТС и остальными контрактами заметно меньше и изменить общее направление арбитражной пары гораздо легче. На таком подходе часто основывается идея одностороннего арбитража, когда «легковесное» краткосрочное отклонение не имеет арбитражного перекрытия по противоположной стороне.
Таким образом, парный трейдинг состоит из двух важных этапов: определение коинтегрированной пары для торговли, и статистический анализ расхождений в динамике, которые могут быть компенсированы обратным движением. В прошлых статьях пары рассчитывались при помощи линейной регрессии цен, а расхождение в динамике спреда определялось отклонением от простой средней линии. Но найденный таким образом ряд на практике для торговли далеко не идеален, потому что не обладает должным уровнем стационарности. В этой статье я расскажу о других способах арбитражного перекрытия и более "умных" алгоритмах анализа полученного спреда.
Используя линейную регрессию для формирования портфеля фьючерсов, трейдер ищет такую комбинацию контрактов на акции, которая на истории максимально полно повторяет цену фьючерса на индекс РТС. По своей сути линейная регрессия - частный случай задачи на оптимизацию, при которой минимизируется сумма квадратов отклонений. То есть каждый день сравнивается цена фРТС и портфеля контрактов и вычисляется расхождение в их стоимости. Затем квадраты этих расхождений суммируются и подбираются такие пропорции в портфеле, чтобы эта сумма была наименьшей. Спредом в таком случае является простая разница в цене обеих сторон арбитражной пары. Спред может плавно меняться в достаточно широких пределах, а резкое отклонение может стать поводом для открытия арбитражной позиции.
Но если обычная регрессия - это лишь оптимизация коэффициентов некоей функции, программно реализованная в большинстве аналитических пакетов, то мы легко можем ее повторить в общем и более удобном виде. Идея перекрытия фРТС портфелем фьючерсов основывается на наличии явных зависимостей в динамике обеих сторон, подтвержденных высокой корреляцией и самой сутью индекса. Поэтому можно взять две пары высоко коррелированных акций и скрестить их. В таком случае можно просто провести оптимизацию коэффициентов первой и второй пары, чтобы минимизировать сумму их отклонений. Эта оптимизация будет расширенным аналогом линейной регрессии, где обе стороны являются функциями от двух независимых переменных. Для примера возьмем восьмерку самых ликвидных фьючерсов на ФОРТС: Газпром, ГМК, Лукойл, Роснефть, Сбербанк, Сургут, Урси и ВТБ. Смотрим полученные графики спредов:

В левой части расположен спред пары Сбербанк+Сургут против Газпром+ВТБ. Хорошо видно, что взаимная высокая корреляция контрактов в составе обеих сторон позволила получить качественный и достаточно стационарный спред. В правой части расположен спред Газпром+Сбербанк против Роснефть+ВТБ. Симбиоз нефтегазовых и финансовых компаний также дал в результате вполне пригодный для торговли спред. Примечательно, что ни для комбинации с использованием ГМК или Урси такие спреды не получить. Для этого пришлось бы добавлять в противоположную пару акции компаний-аналогов, например, Полюс-золото для ГМК и Ростелеком для Урси.
Такой способ составления синтетических пар позволяет конструировать инструменты с примерно одинаковой ценой и высокой корреляцией динамики. Однако, можно подняться на уровень выше и оптимизировать коэффициенты не по цене, а по доходности. То есть для заданного актива необходимо найти такой портфель, который бы имел аналогичный уровень доходности на тех же промежутках времени. Это можно сделать, используя ту же линейную регрессию или популярный инвестиционный Бета-коэффициент. Главное отличие от рассмотренного выше способа в том, что тут уже используются не цены, а процентные приращения. И на выходе мы будем получать не единицы контрактов, а процентные доли в нужном портфеле.
В прошлых статьях, посвященных парному трейдингу и статистическому арбитражу, я подробно рассматривал этапы подготовки и поиска акций для торговли. В общем виде торговля спредом сводится к выделению стационарного ряда из двух или более коинтегрированных инструментов. Такой подход позволяет трейдеру зарабатывать на краткосрочном дисбалансе в доходности или ценах на похожие активы. На пару аналогичных компаний из одного сектора экономики оказывают воздействие одни и те же внешние факторы. А, значит, и реагировать на такие события цены акций должны примерно одинаково. Поэтому краткосрочный дисбаланс в устоявшемся соотношении цен должен быть компенсирован в сторону долгосрочного паритета. Проще говоря, если без видимой причины одна акция показывает резкий рост относительно второй, то можно ожидать его коррекции или догоняющего роста второй акции. Именно фраза "можно ожидать" отличает статистический парный трейдинг от гарантированного математического арбитража. В таком случае временный дисбаланс, скорее всего, будет ликвидирован, но вовсе не обязательно. Мне пришло несколько похожих писем с просьбой объяснить различия между статистическим и математическим арбитражем, и корреляцией и коинтеграцией, поэтому с них и начну.
Математический арбитраж возможен только между инструментами, которые связаны между собой однозначной математической формулой. Например, цена фьючерса вполне конкретно определяется через три переменные: цену акции, безрисковую ставку и срок жизни контракта. Поэтому краткосрочные изменения в цене базовой акции должны моментально отражаться на цене фьючерса. Именно "должны" и никак иначе. В момент экспирации цены акции и фьючерса должны сойтись в одной точке просто по определению фьючерса. Поэтому любое отклонение цены фьючерса от строгого математического закона обязательно будет компенсировано. Можно провести аналогию с двумя автобусами, которые одновременно выезжают из точки А и должны одновременно приехать в точку Б. Они уже выехали - это факт, должны приехать одновременно - для обоих водителей это закон. И если один автобус в дороге задержится и отстанет, то тогда будут возможны три варианта развития событий:
- отстающий водитель увеличивает скорость и догоняет коллегу;
- опережающий водитель притормаживает и ждет;
- отстающий немного ускоряется, а опережающий немного сбавляет скорость и позволяет себя догнать.
Как видим, оба водителя могут манипулировать только скоростью своего автобуса. Но не известно, какой из этих трех вариантов они выберут. Поэтому для получения прибыли трейдеру необходимо "купить скорость" отстающего и одновременно "продать скорость" опережающего. Тогда любой из трех вариантов окажется выигрышным, ведь автобусы обязательно начнут сближение.
Чтобы объяснить суть статистического арбитража и разницу между корреляцией и коинтеграцией, приведу другую аналогию. Представим себе двух братьев, которые бегут на озеро и держат в руках достаточно длинную и упругую пружину. Один конец которой находится у первого, другой - у второго брата. Они оба бегут в одном направлении - это высокая корреляция. А то, что пружина не даст им заметно удалиться друг от друга - это коинтеграция. Какие бы зигзаги они не совершали, какой бы берег они не выбрали, их динамика движения и расстояние между ними будет определяться исключительно упругостью пружины. В этом случае вектор их перемещения примерно одинаков, но расстояние между ними на протяжении всего пути может заметно разниться. В среднем оно равно как раз длине пружины. И чем сильнее они растягивают или сжимают пружину, тем более вероятно, что она вернется к своему исходному состоянию. В этом случае переменным фактором является степень натяжения и длина пружины. Прибыль делается за счет "продажи слишком растянутой пружины" или "покупки слишком сжатой". Ставка делается на то, что рано или поздно длина пружины вернется в исходное состояние. Но проблема в том, что мы заранее не знаем ни предела натяжения пружины ни ее обычной длины, и растягивается она порой легче, чем можно себе представить. Поэтому трейдер не может сказать, что вот здесь и сейчас "степень натяжения" уже чрезмерна. Можно лишь оценить вероятность возврата к средним значениям на основании статистического анализа исторических данных. И открывая позицию, трейдер не может быть на 100% уверен в прибыли.
Частным случаем статистического арбитража является торговля парой "фьючерс РТС против портфеля фьючерсов на акции", который я рассматривал в прошлый раз. Портфель фьючерсов составлялся таким образом, чтобы его стоимостное выражение равнялось цене индексного контракта. Таким образом, получалась ситуация, когда более "тяжелый" фРТС перекрывался более "легкими" фьючерсами на акции. И часто при подобном выборе торговой пары прибыль образовывалась за счет одной-двух акций, выбившихся из общей динамики. Если в классическом арбитраже или парном трейдинге обе стороны сделки равноправны и их движения равновероятны, то тут иногда проявляется некоторая определенность. То есть можно с большей уверенностью говорить, за счет какой стороны или акции будет компенсирован ценовой дисбаланс. Чтобы это пояснить, приведу третью аналогию. Представим себе человека, который гуляет по парку, ведя на поводках трех собак разного размера. В основном, траекторию движения этой четверки определяет хозяин, а собаки образуют вокруг него броуновское движение. Его масса заметно больше и свое направление он изменит только в том случае, если все три собаки вместе потянут в одну сторону. Если же только одна из них куда-то тянет, то в скором времени ей придется подчиниться и вернуться в общий строй. Так и на бирже, только "весовое" различие между фРТС и остальными контрактами заметно меньше и изменить общее направление арбитражной пары гораздо легче. На таком подходе часто основывается идея одностороннего арбитража, когда «легковесное» краткосрочное отклонение не имеет арбитражного перекрытия по противоположной стороне.
Таким образом, парный трейдинг состоит из двух важных этапов: определение коинтегрированной пары для торговли, и статистический анализ расхождений в динамике, которые могут быть компенсированы обратным движением. В прошлых статьях пары рассчитывались при помощи линейной регрессии цен, а расхождение в динамике спреда определялось отклонением от простой средней линии. Но найденный таким образом ряд на практике для торговли далеко не идеален, потому что не обладает должным уровнем стационарности. В этой статье я расскажу о других способах арбитражного перекрытия и более "умных" алгоритмах анализа полученного спреда.
Используя линейную регрессию для формирования портфеля фьючерсов, трейдер ищет такую комбинацию контрактов на акции, которая на истории максимально полно повторяет цену фьючерса на индекс РТС. По своей сути линейная регрессия - частный случай задачи на оптимизацию, при которой минимизируется сумма квадратов отклонений. То есть каждый день сравнивается цена фРТС и портфеля контрактов и вычисляется расхождение в их стоимости. Затем квадраты этих расхождений суммируются и подбираются такие пропорции в портфеле, чтобы эта сумма была наименьшей. Спредом в таком случае является простая разница в цене обеих сторон арбитражной пары. Спред может плавно меняться в достаточно широких пределах, а резкое отклонение может стать поводом для открытия арбитражной позиции.
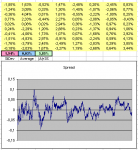
Но если обычная регрессия - это лишь оптимизация коэффициентов некоей функции, программно реализованная в большинстве аналитических пакетов, то мы легко можем ее повторить в общем и более удобном виде. Идея перекрытия фРТС портфелем фьючерсов основывается на наличии явных зависимостей в динамике обеих сторон, подтвержденных высокой корреляцией и самой сутью индекса. Поэтому можно взять две пары высоко коррелированных акций и скрестить их. В таком случае можно просто провести оптимизацию коэффициентов первой и второй пары, чтобы минимизировать сумму их отклонений. Эта оптимизация будет расширенным аналогом линейной регрессии, где обе стороны являются функциями от двух независимых переменных. Для примера возьмем восьмерку самых ликвидных фьючерсов на ФОРТС: Газпром, ГМК, Лукойл, Роснефть, Сбербанк, Сургут, Урси и ВТБ. Смотрим полученные графики спредов:
В левой части расположен спред пары Сбербанк+Сургут против Газпром+ВТБ. Хорошо видно, что взаимная высокая корреляция контрактов в составе обеих сторон позволила получить качественный и достаточно стационарный спред. В правой части расположен спред Газпром+Сбербанк против Роснефть+ВТБ. Симбиоз нефтегазовых и финансовых компаний также дал в результате вполне пригодный для торговли спред. Примечательно, что ни для комбинации с использованием ГМК или Урси такие спреды не получить. Для этого пришлось бы добавлять в противоположную пару акции компаний-аналогов, например, Полюс-золото для ГМК и Ростелеком для Урси.
Такой способ составления синтетических пар позволяет конструировать инструменты с примерно одинаковой ценой и высокой корреляцией динамики. Однако, можно подняться на уровень выше и оптимизировать коэффициенты не по цене, а по доходности. То есть для заданного актива необходимо найти такой портфель, который бы имел аналогичный уровень доходности на тех же промежутках времени. Это можно сделать, используя ту же линейную регрессию или популярный инвестиционный Бета-коэффициент. Главное отличие от рассмотренного выше способа в том, что тут уже используются не цены, а процентные приращения. И на выходе мы будем получать не единицы контрактов, а процентные доли в нужном портфеле.