FXWizard
Гуру форума
Прогнозирование финансовых рынков. Нейросети. Однослойный персептрон.
В данной публикации хочу продемонстрировать работу самой простой нейронной сети - однослойного персептрона к прогнозированию финансовых рынков. Что такое однослойный персептрон (есть мнение, что правильнее перцептрон)?
Автор персептрона (F.Rosenblatt, 1957) рассматривал своё изобретение, как некоторую модель работы мозга. Но не будем останавливаться на биологических особенностях нейросетей.
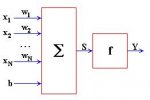
Итак, однослойный персептрон. Схема персептрона представлена ниже.

x[k] - входные элементы (если говорить о финансовых рынках ими могут выступать цены, значения индикаторов, макроэкономические показатели и т.д.);
w[k] - веса (это те элементы, которые необходимо определить);
S=x[1]*w[1]+x[2]*w[2]+...+x[n]*w[n];
f - это функция активации (видов функций активации очень много, самый простой пример: если z>0, то f(z)=1, если z<0, то f(z)=0);
Y=f(S), это выход сети (если говорить о финансовых рынках, то выходами могут выступать как и в случае входов - цены, значения индикаторов, макроэкономические показатели и т.д.);
b - это сдвиг (во многих случаях его принимают равным 0, сделаем так и мы).
Теперь о том, как использовать эту схему для прогнозирования. В данной публикации рассматриваются котировки форекс (forex) - дневные цены закрытия EURUSD.
1. Берем данные и нормируем. В нашем случае (с EURUSD) цены закрытия обрабатывались функцией g(Close[j])=1/(1+e^(-Close[j]))=x[j]. Это нужно для того, чтобы данные были в интервале [-1;1].
2. Разбиваем полученные значения на 2 части - обучающую выборку и проверочную (в случае с EURUSD обучающая выборка составила 29 значений). Определяемся с количеством элементов, подаваемых на вход сети, то есть с количеством иксов (в примере выбрано 10 иксов). Количество весов равно количеству иксов.
3. Присваиваем весам случайные значения (по своему скромному опыту - лучше брать сначала 0).
4. Считаем S.
5. Считаем Y. Как писалось выше Y=f(S). Для EURUSD в качестве f выступала уже известная функция g(S)=1/(1+e^(-S)). Получили некоторое значение Y. Так как нас интересует значение Y, которое является нормированной ценой закрытия, на 11-м шаге (наш прогноз), то мы сравниваем полученное Y на 11-м шаге с реальной (известной нам) нормированной ценой закрытия на 11-м шаге. Безусловно, что вначале они не совпадают. Поэтому мы берём и считаем ошибку путём вычитания из реального значения полученного. Дальше с теми же весами "смещаемся вправо" на один шаг и рассчитываем S=x[2]*w[1]+x[3]*w[2]+...+x[11]*w[10], дальше Y. Потом снова считаем ошибку прогноза на 12 шаге. И так продолжаем до конца обучающей выборки (то есть до 30 элемента). Получили 19 ошибок, которые необходимо просуммировать и поделить на 19 (эта "конечная" ошибка запоминается).
6. Дальше, по формуле w[p+1]=w[p]+h*e(p)*x(p) происходит коррекция весов.
e(p) - нам известно (это "конечная" ошибка, посчитанная на предыдущем шаге), w - это веса (нужно отметить, что порядковые номера остаются неизменными, то есть от 1 до 10, тут показано, что p+1 - это значит все 10 значений изменились, то есть p - это счётчик итераций), x[p] - это те же иксы с порядковыми номерами от 1 до 10 в случае если прогноз на 11-м шаге не совпал с реальным значением (если произошло совпадение, то иксы сдвигаются "вправо" на один шаг), h - число, которое влияет на скорость обучения (выбирается произвольно в зависимости от ситуации - в случае с EURUSD h=0,4). Итерация завершена.
7. Переходим на шаг 4. Если на шаге 5, полученная "конечная" ошибка больше чем ошибка на предыдущей итерации, то процесс обучения заканчивается и искомыми весами будут веса, полученные на предыдущей итерации. Таким образом получаем 10 весов и нам известно 10 иксов, считаем S, а потом считаем Y - это и будет наш прогноз на один шаг.
Вернёмся к нашему конкретному примеру. Была написана программка, которая реализует вышеописанное и ниже представлен график из программки с двумя кривыми - красной (прогноз на один шаг) и зелёной (реальные значения).

Как видно из графика, нейросеть на основе однослойного персептрона, мягко говоря, не очень хорошо прогнозирует финансовые ряды.
Вывод: модель в рассмотренном формате (когда брались только цены закрытия и вышеизложенный метод коррекции весов) непригодна для прогнозирования финансовых временных рядов.
От себя добавлю. Как вариант, для обучения (подбора весов) однослойного персептрона скорее всего лучше использовать генетические алгоритмы.
Источник
В данной публикации хочу продемонстрировать работу самой простой нейронной сети - однослойного персептрона к прогнозированию финансовых рынков. Что такое однослойный персептрон (есть мнение, что правильнее перцептрон)?
Автор персептрона (F.Rosenblatt, 1957) рассматривал своё изобретение, как некоторую модель работы мозга. Но не будем останавливаться на биологических особенностях нейросетей.
Итак, однослойный персептрон. Схема персептрона представлена ниже.
x[k] - входные элементы (если говорить о финансовых рынках ими могут выступать цены, значения индикаторов, макроэкономические показатели и т.д.);
w[k] - веса (это те элементы, которые необходимо определить);
S=x[1]*w[1]+x[2]*w[2]+...+x[n]*w[n];
f - это функция активации (видов функций активации очень много, самый простой пример: если z>0, то f(z)=1, если z<0, то f(z)=0);
Y=f(S), это выход сети (если говорить о финансовых рынках, то выходами могут выступать как и в случае входов - цены, значения индикаторов, макроэкономические показатели и т.д.);
b - это сдвиг (во многих случаях его принимают равным 0, сделаем так и мы).
Теперь о том, как использовать эту схему для прогнозирования. В данной публикации рассматриваются котировки форекс (forex) - дневные цены закрытия EURUSD.
1. Берем данные и нормируем. В нашем случае (с EURUSD) цены закрытия обрабатывались функцией g(Close[j])=1/(1+e^(-Close[j]))=x[j]. Это нужно для того, чтобы данные были в интервале [-1;1].
2. Разбиваем полученные значения на 2 части - обучающую выборку и проверочную (в случае с EURUSD обучающая выборка составила 29 значений). Определяемся с количеством элементов, подаваемых на вход сети, то есть с количеством иксов (в примере выбрано 10 иксов). Количество весов равно количеству иксов.
3. Присваиваем весам случайные значения (по своему скромному опыту - лучше брать сначала 0).
4. Считаем S.
5. Считаем Y. Как писалось выше Y=f(S). Для EURUSD в качестве f выступала уже известная функция g(S)=1/(1+e^(-S)). Получили некоторое значение Y. Так как нас интересует значение Y, которое является нормированной ценой закрытия, на 11-м шаге (наш прогноз), то мы сравниваем полученное Y на 11-м шаге с реальной (известной нам) нормированной ценой закрытия на 11-м шаге. Безусловно, что вначале они не совпадают. Поэтому мы берём и считаем ошибку путём вычитания из реального значения полученного. Дальше с теми же весами "смещаемся вправо" на один шаг и рассчитываем S=x[2]*w[1]+x[3]*w[2]+...+x[11]*w[10], дальше Y. Потом снова считаем ошибку прогноза на 12 шаге. И так продолжаем до конца обучающей выборки (то есть до 30 элемента). Получили 19 ошибок, которые необходимо просуммировать и поделить на 19 (эта "конечная" ошибка запоминается).
6. Дальше, по формуле w[p+1]=w[p]+h*e(p)*x(p) происходит коррекция весов.
e(p) - нам известно (это "конечная" ошибка, посчитанная на предыдущем шаге), w - это веса (нужно отметить, что порядковые номера остаются неизменными, то есть от 1 до 10, тут показано, что p+1 - это значит все 10 значений изменились, то есть p - это счётчик итераций), x[p] - это те же иксы с порядковыми номерами от 1 до 10 в случае если прогноз на 11-м шаге не совпал с реальным значением (если произошло совпадение, то иксы сдвигаются "вправо" на один шаг), h - число, которое влияет на скорость обучения (выбирается произвольно в зависимости от ситуации - в случае с EURUSD h=0,4). Итерация завершена.
7. Переходим на шаг 4. Если на шаге 5, полученная "конечная" ошибка больше чем ошибка на предыдущей итерации, то процесс обучения заканчивается и искомыми весами будут веса, полученные на предыдущей итерации. Таким образом получаем 10 весов и нам известно 10 иксов, считаем S, а потом считаем Y - это и будет наш прогноз на один шаг.
Вернёмся к нашему конкретному примеру. Была написана программка, которая реализует вышеописанное и ниже представлен график из программки с двумя кривыми - красной (прогноз на один шаг) и зелёной (реальные значения).
Как видно из графика, нейросеть на основе однослойного персептрона, мягко говоря, не очень хорошо прогнозирует финансовые ряды.
Вывод: модель в рассмотренном формате (когда брались только цены закрытия и вышеизложенный метод коррекции весов) непригодна для прогнозирования финансовых временных рядов.
От себя добавлю. Как вариант, для обучения (подбора весов) однослойного персептрона скорее всего лучше использовать генетические алгоритмы.
Источник