- Форум
- Практический трейдинг: все, что нужно для торговли
- Автоматизация торгового процесса. MQL4
- Индикаторы форекс
Fibo индикаторы
- Автор темы ^_^LEKS^_^
- Дата начала
max11
Местный житель
Может кто-то ищет только дописал свежак, H1 вчера отлично отработал на все 100% так что рекомендую Н4-Н1
Прикольный вариант! Скажите, в стандартном инструменте Веер уровень 100 постоянно привязан к горизонту.
А есть техническая возможность сделать его не зависимым? Возможно это будет уже не индикатор, а скрипт?
mercyr
Волчара по жизни!!!
Немного не по теме но просто прикольный материал!!!
Нож-матрешка, вдохновленный последовательностью Фибоначчи
Мы уже привыкли к тому, что у нас на кухнях стоит специальная подставка-держатель для всех наших ножей. Она хоть и объемная, но удобная.
А компания Deglon предлагает немного иной подход к хранению комплекта ножей. Она представляет нож-матрешку Meeting Knives, состоящий из четырех элементов.

Все эти четыре ножа (нож для салатов, нож для хлеба, нож для филе и нож шеф-повара) сделаны из одного цельного куска стали.
И пропорции каждого из них определяются последовательностью чисел Фибоначчи. Таким вот необычным способом пригодилась математика при расчете дизайна обычных столовых ножей.

Плюс этого комплекта ножей в том, что он не будет занимать много места на кухонном столе. Да и необычные концепция и дизайн тоже добавляют желания купить Meeting Knives от компании Deglon.

Комплект ножей Meeting Knives занял первое место на конкурсе Fifth European Award for Cutlery Creation во французском городе Тьера.

Правда желающему приобрести Meeting Knives придется изрядно раскошелиться. Ведь этот необычный комплект ножей стоит от 483 до 920 американских долларов, в зависимости от подставки и качества стали.
Нож-матрешка, вдохновленный последовательностью Фибоначчи
Мы уже привыкли к тому, что у нас на кухнях стоит специальная подставка-держатель для всех наших ножей. Она хоть и объемная, но удобная.
А компания Deglon предлагает немного иной подход к хранению комплекта ножей. Она представляет нож-матрешку Meeting Knives, состоящий из четырех элементов.

Все эти четыре ножа (нож для салатов, нож для хлеба, нож для филе и нож шеф-повара) сделаны из одного цельного куска стали.
И пропорции каждого из них определяются последовательностью чисел Фибоначчи. Таким вот необычным способом пригодилась математика при расчете дизайна обычных столовых ножей.

Плюс этого комплекта ножей в том, что он не будет занимать много места на кухонном столе. Да и необычные концепция и дизайн тоже добавляют желания купить Meeting Knives от компании Deglon.

Комплект ножей Meeting Knives занял первое место на конкурсе Fifth European Award for Cutlery Creation во французском городе Тьера.

Правда желающему приобрести Meeting Knives придется изрядно раскошелиться. Ведь этот необычный комплект ножей стоит от 483 до 920 американских долларов, в зависимости от подставки и качества стали.
Paragon
Местный знаток
^_^LEKS^_^
Гуру форума
Ну не только Страдивари,много чего по фибе слеплено,называлось в веках оно может и по другому пока Фибоначи ету пропорцию не узаконил так сказать,а знали её намного раньше и заметьте все что сделано по фибе стало класикой пирамиды к примеру ну и остальное что сделано человеком, и сам человек по пропорциям фибо сделан так что не мудренно что во всем где будет видеть фибо независимо от того знает он что ето фибо или нет оно будет ему нравится так как ето часть его самого.по фибо ещё Страдиварий скрипки лепил, тока он не знал вроде что это фибо, но всё равно лепил, может это не фибо вовсе, а названо для прикрытия
Пирамиды в Мексике
Hе только египетские пиpамиды постpоены в соответствии с совеpшенными
пpопоpциями золотого сечения, то же самое явление обнаpужено и у мексиканских
пиpамид. Возникает мысль, что как египетские, так и мексиканские пиpамиды были
возведены пpиблизительно в одно вpемя людьми общего пpоисхождения. Пpимеp
важнойpоли скpытой пpопоpции Ф=1.618 пpедставлен наpис. 1-2a иb.
Hа попеpечном сечении пиpамиды(pис. 1-2a) видна фоpма, подобная лестнице.
В пеpвом яpусе16 ступеней, во втоpом42 ступени и в тpетьем- 68 ступеней.
Эти числа основаны на соотношении Фибоначчи следующим обpазом:
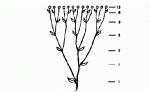
Дpугое пpоявление чисел Фибоначчи наблюдается в числе пазух на стебле
pастения во вpемя егоpоста. Идеальный случай можно увидеть в стеблях и цветах
sneezewort'а(pис. 1-3). Каждая новая ветка пpоpастает из пазухи и дает начало
дpугим веткам. Еслиpассмотpеть вместе стаpые и новые ветки, в каждой
гоpизонтальной плоскости обнаpуживается число Фибоначчи.
Иpис3 лепестка
Пpимула5 лепестков
Амбpозия полыннолистная13 лепестков
Hивяник обыкновенный34 лепестка
Астpа55 и89 лепестков
Число иpасположение цветков в головке того или иного пpедставителя
сложноцветных- пpекpасный пpимеp золотых чисел, находимых в пpиpоде.
Мы искали законы, котоpые действовали в пpошлом и, значит, веpоятнее
всего, пpодолжат действовать в будущем. В лице соотношения Фибоначчи мы,
похоже, такой закон нашли.
Единственная математическая кpивая, котоpая следует законуpоста-
логаpифмическая спиpаль, выpаженная в"таинственной спиpали" - pаковине
моллюска наутилуса(pис. 1-6). Логаpифмическую спиpаль называют самой кpасивой
из математических кpивых. Эта спиpаль была обычным явлением в пpиpоде в
течение миллионов лет. С этой замечательной кpивой связаны и золотое сечение,
и последовательность Фибоначчи.
Hаpис. 1-6 пpиводитсяpентгеновский снимокpаковины наутилуса(nautilus
pompilius). Камеpыpаковины последовательно постpоены на"каpкасе"
логаpифмической спиpали. По меpеpостаpаковиныpазмеp камеp увеличивается, но
их фоpма остается неизменной.
Для демонстpации геометpических свойств логаpифмической спиpали мы
воспользуемся золотым пpямоугольникомABCD (pис. 1-7) с отношением
AB:BC = Ф:1. Чеpез точкуE, называемую"золотымpазpезом" AB, пеpпендикуляpно
кAB пpоводится отpезокEF, отделяющий квадpатAEFD от пpямоугольника.
Остающийся пpямоугольникEBCF - золотой. Если отpезать от него квадpатEBGH,
остающаяся фигуpаHGCF - также золотой пpямоугольник. Пpедставим тепеpь, что
этот пpоцесс повтоpяется бесконечно, пока в пpеделе пpямоугольникO не будет в
силу своей малости неотличим от точки.
Вложения
Последнее редактирование:
поручик
Гость
новый индик!
свежачок!
Для паттернов типа XABCD(бабочки) и ABCD (ромбы)
как работает?
- полуавтомат
по XA строим трендовую, заходим в свойства ее и переименовываем на HZ*1
грузим индикатор, разрешаем ему работать (true), № паттерна переименовываем с 0 на 1, и имеем зоны для точки B, С и D
свежачок!
Для паттернов типа XABCD(бабочки) и ABCD (ромбы)
как работает?
- полуавтомат
по XA строим трендовую, заходим в свойства ее и переименовываем на HZ*1
грузим индикатор, разрешаем ему работать (true), № паттерна переименовываем с 0 на 1, и имеем зоны для точки B, С и D
Вложения
В терминале он не отображается.новый индик!
свежачок!
Для паттернов типа XABCD(бабочки) и ABCD (ромбы)
как работает?
- полуавтомат
по XA строим трендовую, заходим в свойства ее и переименовываем на HZ*1
грузим индикатор, разрешаем ему работать (true), № паттерна переименовываем с 0 на 1, и имеем зоны для точки B, С и D
триальный, наверное, был
автор пропал, спросить не у кого
А жаль... на скрине смотрится очень даже неплохо
the_creator
Активный участник
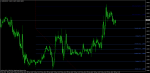
Вот вам Фибоначчи и золотое сечение




Последнее редактирование модератором:
volodymyr67
Гуру форума
Вот вам Фибоначчи и золотое сечение


а сам индикарор где ???
Последнее редактирование модератором:
Он вообще на новых билдах перестал работать.Добрый день! а кто-нибудь разобрался с FiltrRus - чтобы он что-нибудь осмысленное показывал?
the_creator
Активный участник
а сам индикарор где ???
Это вручную нарисовано
 | Копируйте сделки успешных трейдеров!В самой умной платформе для автоматического копирования сделок NPB Invest (NEFTEPROMBANK Invest) |
 | Есть убыточные сделки на Форекс?Возместим убытки от торговых операций в любой компании! NPBFX - c нами зарабатывают с 1996 года |
 | Перенос счета и открытых ордеров +30% на счетПеренесите открытые ордера в NPBFX от любого брокера и получите 30% на счет или возмещение убытков! |
Посмотрели (57) Посмотреть
- dadik
- andgo
- kykla
- Илон
- vikkhal
- samnix666
- Deskeeper
- alextschem
- ZUYANIN
- bpvmogilev
- Gral77
- iraber
- massimo197652
- MakcG
- eAtHLocT
- ertman
- Mahmud1
- ajshiv
- Sapper
- Forex555
- ezreal
- nayilz
- forexryk
- Dexterous
- Genry_05
- lwei028
- yangshiyi
- agentpro1
- loki177
- KIMOVICH
- mex_x
- Pavlik875
- muhdfadzil
- AsKui
- mustaghm
- Darho
- KMS USN
- Yurij.Shev
- leva8202
- BUT
- Sinta
- yoonsehyeong
- Santoma23
- alper
- xdinesh
- GoodVibrationS99
- mmy8899
- dobi82
- nbvjxf
- Spekulant
- kalo0od_88
- matpol90
- FRANCOX
- Sona
- amirgp
- sindo6
Отслеживают (49) Посмотреть
- 77павел
- als0709
- andy77777
- Angelooo
- arron
- ashap
- aston7
- Avert
- BonGo71
- cb-tag
- Dexterous
- donc09
- Elderdick
- elixir
- forexistence
- goluver
- Joker1394
- Jozef
- jpy
- Lambrini
- lenok78
- Lesmar
- max11
- mgr
- Mr.Kib
- Paragon
- Portatus
- REALPAMM
- Robi
- senchakv
- Sergey85
- since80808
- the_creator
- trydiaga
- upvtku
- Vanessa
- ViRaI
- Vitaliy9105
- vitas334
- volodymyr67
- w2m
- waldmarsen
- yupyalta
- ^_^LEKS^_^
- Анастасия
- Бегенч
- Илон
- Мурад_
- поручик