Ральф Винс. Математика управления капиталом

[FXWizard]

Одиночная позиция по базовому инструменту

В главе 3 мы подробно рассмотрели математику поиска оптимального f параметрическим способом. Теперь мы можем использовать тот же метод и для одиночной длинной опционной позиции с учетом нового HPR, которое рассчитывается по уравнению (3.30):

где HPR(U) = HPR для данного U;
L= ассоциированное P&L;
W = ассоциированное P&L худшего случая (это всегда отрицательное значение);
f == тестируемое значение f;
Р = ассоциированная вероятность.

Для длинной позиции переменная L, т.е. ассоциированное P&L, определяется как разность между ценой базового инструмента U и ценой S.

(5.21 а) L для длинной позиции = U - S

Для короткой позиции ассоциированное P&L рассчитывается наоборот:

(5.216) L для короткой позиции = S - U,

где S = текущая цена базового инструмента;
U = цена базового инструмента для данного HPR.
Мы можем также рассчитать оптимальное f для одиночной позиции по базовому инструменту, используя уравнение (5.14). При этом надо иметь в виду, что оптимальное f может получиться больше 1.
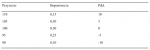
Пусть цена базового инструмента равна 100, и мы ожидаем пять результатов:

Отметьте, что исходя из уравнения (5.10) наше арифметическое математическое ожидание по базовому инструменту составляет 100,576923077. Это означает, что переменная Y для (5.14) равна 0,576923077, так как 100,576923077-100= = 0,576923077. Если рассчитать оптимальное f, используя столбец P&L и уравнение (3.30), мы получим f= 1,9, что соответствует 1 единице на каждые 52,63 доллара на счете. Если в уравнении (5.14) использовать данные из столбца «Результат», тогда переменная S равна 100. В этом случае мы не вычитаем значение Y (арифметическое математическое ожидание базового инструмента минус его текущая цена) из U при определении переменной Z(T, U - Y), и получаем оптимальное f около 1,9, что соответствует 1 единице на каждые 52,63 доллара на счете, так как 100 /1,9=52,63.
Если вычесть значение Y в выражении Z(T, U - Y), являющемся элементом уравнения (5.14), мы получим математическое ожидание по базовому инструменту, равное его текущему значению, и поэтому f не будет оптимальным.
Тем не менее нам следует вычесть значение Y в Z(T, U - Y) для того, чтобы соответствовать расчетам цен опционов, а также формуле «пут-колл» паритета.
Если мы будем использовать уравнение (3.30) вместо уравнения (5.14), тогда из каждого значения U в (5.21а) и (5.216) следует вычесть значение Y, то есть надо вычесть Y из каждого P&L, что опять же создает ситуацию, когда нет положительного математического ожидания, и поэтому нет оптимального значения f. Все вышесказанное означает, что если мы откроем позицию по базовому инструменту, не имея никаких представлений о направлении движения его цены, то не получим положительного математического ожидания (как происходит с некоторыми опционами) и поэтому не найдем оптимального f. Мы можем получить оптимальное f только в том случае, когда математическое ожидание положительное. Это произойдет, если базовый инструмент «в тренде».
Теперь у нас есть методология, позволяющая определить оптимальное f (и его побочные продукты) для опционов и базового инструмента (разными способами).
Отметьте, что используемые в этой главе методы определения оптимальных f и побочных продуктов для опционов или базового инструмента не требуют обязательного применения механической системы. Вспомним, что эмпирический метод поиска оптимального f основан на эмпирическом потоке P&L, созданном механической системой. Из главы 3 мы узнали о параметрическом методе поиска оптимального f на основе данных, которые имеют нормальное распределение. Тот же метод можно использовать для поиска оптимального f при любом распределении данных, если существует функция распределения. Из главы 4 мы познакомились с параметрическим методом поиска оптимального f для распределений торговых P&L, которые не имеют функций распределения (длямеханической или немеханической системы) и с методом планирования сценария.

 

[FXWizard]

В этой главе мы изучили метод поиска оптимального f для немеханических систем. Обратите внимание, все расчеты допускают, что вы в некоторый момент времени «слепо» открываете позицию, причем направленного движения цены базового инструмента не ожидается. Таким образом, предложенный метод лишен какого-либо прогноза относительно цены базового инструмента. Мы увидели, что можно учесть ценовой прогноз, изменяя каждый день значение базового инструмента в уравнениях 5.17а и 5.176. Даже слабый тренд значительно меняет функцию ожидания. Оптимальная дата выхода может не быть теперь рыночным днем сразу после дня входа, более того, оптимальная дата выхода может стать датой истечения срока. В таком случае опцион будет иметь положительное математическое ожидание, даже если его держать до даты истечения. При небольшом тренде цены базового инструмента значительно изменится не только функция ожидания, но и оптимальные f, AHPR и GHPR.
Проиллюстрируем вышесказанное на следующем примере. Пусть цена исполнения колл-опциона равна 100 и он истекает 911120, цена базового инструмента равна также 100. Волатильность составляет 20%, а сегодняшняя дата 911104. Мы будем использовать формулу товарных опционов Блэка (Н находим из уравнения (5.07), R = 5%) и 260,8875-дневный год. Для 8 стандартных отклонений рассчитаем оптимальные f (чтобы соответствовать прошлым таблицам, которые не учитывают тренд по базовому инструменту), и используем минимальное приращение тика 0,1. В данном случае мы будем учитывать тренд, при котором цена базового инструмента растет на 0,01 пункта (одну десятую тика) в день:

Отметьте, как небольшой тренд (0,01 пункта в день) меняет результаты. Наша оптимальная дата выхода остается 911105, но оптимальное f= 0,1081663, что соответствует 1 контракту на каждые 2645 долларов на балансе счета (2,861* * 100 / 0,1081663). Кроме того, для этого опциона ожидание положительно все время до 911107. Если тренд будет сильнее, результаты изменятся еще больше. Последнее, что необходимо учесть, — это размер комиссионных. Цена опциона из уравнения (5.14) (значение переменной Z(T, U - Y)) должна быть уменьшена на размер комиссионных (если с вас берут комиссионные и при открытии позиции, то вы должны увеличить значение переменной S из уравнения (5.14) на размер комиссионных).
Мы рассмотрели поиск оптимального f и его побочных продуктов, когда механическая система не используется. Теперь перейдем к изучению одновременной торговли по нескольким позициям.

 

[FXWizard]

Торговля по нескольким позициям при наличии причинной связи

Прежде чем начать обсуждение одновременной торговли по нескольким позициям, необходимо пояснить разницу между причинными связями и корреляционными связями. В случае с причинной связью существует фактическое, связующее объяснение корреляции между двумя или более событиями, т. е. причинная связь — это такое отношение, где есть корреляция, и ее можно объяснить логически.
Обычная корреляционная связь подразумевает, что есть зависимость, но этому нет причинного объяснения. В качестве примера причинной связи давайте рассмотрим пут-опционы и колл-опционы на акции IBM. Очевидно, что корреляция между пут и колл-опционами IBM составляет -1 (или находится очень близко к этому значению), но эта связь означает больше, чем просто корреляция. Мы знаем, что, когда по колл-опционам IBM возникает давление вверх, появляется давление и вниз по пут-опционам (все остальное считается постоянным, включая волатильность). Описанное логическое связующее отношение означает, что между пут и колл-опционами IBM существует причинная связь.
Когда существует корреляция, но нет причины, мы просто говорим, что есть корреляционная связь (в противоположность причинной связи). Обычно при корреляционной связи коэффициент корреляции (по абсолютной величине) меньше 1, как правило, абсолютное значение коэффициента корреляции ближе к 0.
Например, цены на кукурузу и соевые бобы в большинстве случаев движутся параллельно. Хотя их коэффициенты корреляции не равны точно 1, существует причинная связь, так как оба рынка реагируют на события, которые затрагивают зерновые. Если мы рассматриваем колл-опционы IBM и пут-опционы компании Digital Equipment (или колл-опционы), мы не можем сказать, что между ними существует четкая причинная связь. Что-то от причинной связи в этом случае безусловно есть, так как оба вида базового инструмента (акции) входят в
компьютерную группу, но только потому, что цена IBM растет (или падает), акции Digital Equipment не обязательно должны расти или падать. Как видите, нет четкой грани, которая разделяет причинные и корреляционные связи.
Невозможность четкого определения вида связи создает некоторые проблемы в работе. Сначала мы рассмотрим только причинные связи, или те, которые, как мы полагаем, являются причинными. В следующей главе мы обсудим корреляционные связи, которые включают также и причинные связи. Вы должны понимать, что методы, упомянутые в следующей главе в отношении корреляционных связей, применимы и для причинных связей. Обратное не всегда верно.
Применение методов, используемых для причинных связей, в случае, когда связи просто корреляционны, является ошибкой. Причинная связь подразумевает, что коэффициенты корреляции между ценами двух объектов составляют 1 или -1. Для упрощения будем считать, что причинная связь затрагивает два инструмента (акция, товар, опцион и т.д.), имеющих один базовый инструмент. Это могут быть спрэды, стредлы, «покрытая продажа» или любая другая позиция, когда вы используете базовый инструмент совместно с одним или более опционами или один или несколько опционов по одному базовому инструменту, даже если у вас нет позиции по этому базовому инструменту.
Простейшим примером одновременных позиций является комбинация опционов (т.е. позиция по базовому инструменту отсутствует), когда совокупная позиция заносится в дебет и можно использовать уравнение (5.14). Таким образом, вы можете определить оптимальное f для всей позиции, а также побочные продукты (включая оптимальную дату выхода). В этом случае переменная S выражает общие затраты на сделку, а переменная Z(T, U - Y) выражает «общую» цену всех одновременных позиций при цене базового инструмента U, когда время, оставшееся до истечения срока исполнения, равно Т. Когда совокупная позиция заносится в кредит, можно определить оптимальное f с помощью уравнения (5.20).
Как и в предыдущем случае, мы должны изменить переменные S и Z(T, U - Y) для отражения «чистой» цены всех позиций. Например, мы рассматриваем возможность открытия длинного стредла (покупка пут-опциона и колл-опциона по одному базовому инструменту с одинаковой ценой исполнения и датой истечения). Допустим, что полученное с помощью этого метода оптимальное f соответствует 1 контракту на каждые 2000 долларов. Таким образом, на каждые 2000 долларов на счете мы должны покупать 1 стредл (1 пут-опцион и 1 колл-опцион). Оптимальное f, полученное с помощью данного метода, относится к финансированию 1 единицы для всей позиции. Этот факт касается всех методов, рассмотренных в данной главе. Ниже представлено уравнение для одновременных позиций, причем не имеет значения, используется позиция по базовому инструменту или нет. Мы будем применять эту обобщенную форму для одновременных позиций с причинной связью:

где N = число «ног» (число составляющих сложной позиции);
HPR(T, U) = HPR для тестируемых значений Т и U;
C(T, U) = коэффициент i-ой «ноги» при данном значении U, когда время,
оставшееся до истечения срока, равно Т.
Для опционных «ног», занесенных в дебет, или длинной позиции по базовому инструменту:

Для опционных «ног», занесенных в кредит, или короткой позиции по базовому инструменту:

где f = тестируемое значение f;
S = текущая цена опциона или базового инструмента;
Z(T, U - Y) = теоретическая цена опциона, когда цена базового инструмента равна U - Y, а время, оставшееся до срoка истечения, равно Т;
Р(Т, U) = вероятность того, что базовый инструмент равен U, когда время, оставшееся до истечения срока исполнения, равно Т;
Y = разность между арифметическим математическим ожиданием базового инструмента (согласно уравнению (5.10)) и текущей ценой.
Уравнение (5.22) следует использовать, когда речь идет об одновременно используемых «ногах», и вам необходимо найти оптимальное f и оптимальную дату выхода по всей позиции (т.е. когда речь идет об одновременной торговле по нескольким позициям).
Для каждого значения U вы можете найти HPR с помощью уравнения (5.22), а для каждого значения f вы можете найти среднее геометрическое, составленное из всех HPR, с помощью уравнения (5.18а):

где G(f, Т) = среднее геометрическое HPR для данного тестируемого значения f и для данного времени, остающегося до истечения срока от указанной даты выхода. Значения f и Т, которые дают наивысшее среднее геометрическое, являются значениями, которые следует использовать для всего набора одновременных позиций.
Подведем итог. Нам надо найти оптимальное f для каждого дня (между текущим днем и днем истечения) как дня выхода. Для каждой даты выхода необходимо определить цены между плюс и минус Х стандартных отклонений (обычно Х будет равно 8) от базовой цены базового инструмента. Базовая цена может быть текущей ценой базового инструмента, или же она может быть скорректирована для учета ценового тренда. Теперь вам надо найти значение для f между 0 и 1, которое даст наибольшее среднее геометрическое HPR, используя HPR для цен между
плюс и минус Х стандартных отклонений от базовой цены для указанной даты выхода. Таким образом, для каждой даты выхода у вас будет оптимальное f и соответствующее среднее геометрическое. Дата выхода, которая дает наибольшее среднее геометрическое, является оптимальной датой выхода из позиции, и f, соответствующее этому среднему геометрическому, является оптимальным f.
Структура этой процедуры следующая:

Для каждой даты выхода между текущей датой и датой истечения
Для каждого значения f (пока не будет найдено оптимальное)
Для каждой рыночной системы
Для каждого тика между +8 и -8 стандартными отклонениями
Определите HPR
Следует отметить, что мы можем определить оптимальную дату выхода, т.е. дату,когда следует закрыть всю позицию. Можно применить эту же процедуру для нахождения оптимальной даты выхода для каждой «ноги» (отдельной позиции), что, правда, геометрически увеличит число расчетов. Тогда процедура несколько изменится и будет выглядеть следующим образом:
Для каждой рыночной системы
Для каждой даты выхода между текущей датой и датой истечения
Для каждого значения f (пока не будет найдено оптимальное)
Для каждой рыночной системы
Для каждого тика между +8 и -8 стандартными отклонениями
Определите HPR

Итак, мы рассмотрели одновременную торговлю по нескольким позициям при наличии причинной связи. Теперь рассмотрим ситуацию, когда связь случайна.

 

[FXWizard]

Торговля по нескольким позициям при наличии случайной связи

Вы должны знать, что, как и в случае с причинной связью, методы, упомянутые в следующей главе, посвященной корреляционным связям, применимы и для случайных связей. Но не наоборот. Неправильно применять методы для случайных связей к корреляционным связям (когда коэффициенты корреляции не равны 0). При случайной связи коэффициент корреляции между ценами двух инструментов всегда равен 0.
Случайная связь между двумя торгуемыми инструментами (акции, фьючерсы, опционы и т.д.) имеет место в том случае, если их цены не зависят друг от друга, т.е. коэффициент корреляции цен равен нулю, или ожидается, что он будет равен нулю в асимптотическом смысле.
Когда коэффициент корреляции двух составляющих равен О, HPR для совокупной позиции рассчитывается следующим образом:

где N = число «ног» позиции;
HPR(T, U) = HPR для данного тестируемого значения Т и U;
С. (Т, U) = коэффициент i-ой «ноги» при данном значении U, когда время,
оставшееся до истечения срока, равно Т.
Для опционных «ног», занесенных в дебет, или длинной позиции по базовому инструменту:

Для опционных «ног», занесенных в кредит, или короткой позиции по базовомуинструменту:

где f = тестируемое значение f;
S = текущая цена опциона;
Z(T, U - Y) = теоретическая цена опциона, когда цена базового инструмента равнаU - Y, а время, оставшееся до срока истечения, равно Т;
P j (T, U) = вероятность того, что базовый инструмент равен U, когда время,оставшееся до истечения срока исполнения, равно Т;
Y = разность между арифметическим математическим ожиданием базового инструмента (согласно уравнению (5.10)) и текущей ценой.
Теперь мы можем рассчитать среднее геометрическое HPR для случайной связи:

где G(f, Т) = среднее геометрическое HPR для данного тестируемого значения f и данного времени Т, остающегося до истечения срока от указанной даты выхода.
Значения f и Т, которые дают наибольшее среднее геометрическое, оптимальны.
Структура этой процедуры такая же, как и в случае с причинной связью:

Для каждой даты выхода между текущей датой и датой истечения
Для каждого значения f (пока не будет найдено оптимальное)
Для каждой рыночной системы
Для каждого тика между +8 и -8 стандартными отклонениями
Определите HPR

Единственное различие между процедурой нахождения среднего геометрического для случайных связей и процедурой для причинных связей состоит в том, что показатель степени для каждого HPR при случайной связи рассчитывается путем умножения вероятностей того, что «ноги» будут находиться на данной цене определенного HPR. Все эти суммы вероятностей, используемые в качестве показателей степени для каждого HPR, сами по себе также суммируются, так что, когда все HPR перемножены для получения промежуточного TWR, его можно возвести в степень единицы, деленной на сумму показателей степени, используемых в HPR. И снова процедуру можно изменить, чтобы найти оптимальные даты выхода для каждой составляющей позиции.
Несмотря на всю сложность, уравнение (5.25) все-таки не решает проблему ненулевого коэффициента линейной корреляции между ценами двух компонентов.
Как видите, определение оптимальных весов компонентов является довольно сложной задачей! В следующих нескольких главах вы увидите, как найти правильные веса для каждой составляющей позиции, будь то акция, товар, опцион или любой другой инструмент, независимо от связи (причинная, случайная или корреляционная). Входные данные, которые нам потребуются, следующие: (1) коэффициенты корреляции средних дневных HPR позиций в портфеле на основе 1 контракта, (2) арифметические среднее HPR и стандартные отклонения HPR.

 

[FXWizard]

Уравнения (5.14) и (5.20) показывают, как находить HPR для длинных и
коротких позиций по опционам. Уравнение (5.18) показывает, как находить
среднее геометрическое. Мы можем также определить среднее арифметическое:
Для длинных опционных позиций, т.е. отнесенных в дебет:

Для коротких опционных позиций, т.е. отнесенных в кредит:

где AHPR = среднее арифметическое HPR;
f= оптимальное f (от 0 до 1);
S= текущая цена опциона;
Z(T, U - Y)= теоретическая цена опциона, когда цена базового инструмента равна U - Y, а время, оставшееся до срока истечения, равно Т;
Р(Т, U) = вероятность, что базовый инструмент равен U, когда время, оставшееся до истечения срока исполнения, равно Т;
Y= разность между арифметическим математическим ожиданием базового
инструмента (согласно уравнению (5.10)) и текущей ценой.
Зная среднее геометрическое HPR и среднее арифметическое HPR, можно определить стандартное отклонение значений HPR:

где А = арифметическое среднее HPR;
G = геометрическое среднее HPR;
SD = стандартное отклонение значений HPR.
В этой главе мы познакомились еще с одним способом расчета оптимального f.
Предложенный метод подходит для несистемных трейдеров. В виде входного параметра здесь используется распределение результатов по базовому инструменту к определенной дате в будущем. Данный подход позволяет найти оптимальное f как для отдельных опционных позиций, так и для сложных позиций. Существенным недостатком метода является то, что связи между всеми позициями должны быть случайными или причинными.
Означает ли вышесказанное, что мы не можем использовать методы поиска оптимального f, рассмотренные в предыдущих главах, для нескольких одновременно открытых позиций или опционов? Нет, вы всегда можете выбрать наиболее эффективный с вашей точки зрения подход. Методы, детально описанные в этой главе, имеют как определенные недостатки, так и достоинства (например возможность расчета оптимального времени выхода). В следующей главе мы будем изучать темы, касающиеся построения оптимального портфеля, что позднее поможет нам в управлении капиталом при одновременной торговле по нескольким позициям.
Цель этой книги — изучить портфели рыночных систем, использующих различные инструменты с различных рынков. В данной главе мы достаточно подробно рассмотрели теоретические цены опционов и теперь перейдем к созданию оптимального портфеля.

 

[FXWizard]

Глава 6 Корреляционные связи и выведение эффективной границы

Мы узнали несколько способов поиска оптимального количества при торговле фьючерсами, акциями и опционами (по отдельности или совместно с другими инструментами), когда существует либо случайная, либо причинная связь между ценами инструментов. Можно определить оптимальный набор, когда коэффициент линейной корреляции двух любых элементов портфеля равен 1, - 1 или 0.
Однако связи между двумя элементами портфеля, рассматриваем ли мы корреляцию цен (в немеханической торговой системе) или изменений баланса (в механической системе), редко дают такие удобные значения коэффициентов линейной корреляции. В этой главе описан способ определения эффективной границы портфелей рыночных систем, когда коэффициенты линейной корреляции любых двух компонентов рассматриваемого портфеля принимают произвольные значения между -1 и 1 включительно. Далее описан метод, применяемый профессионалами для расчета оптимальных портфелей акций. В следующей главе мы адаптируем его для использования любых инструментов. Данная глава основана на важном предположении, которое заключается в том, что распределения, генерирующие последовательность сделок (распределения прибылей), имеют конечную дисперсию. Предложенные методы эффективны только тогда, когда используемые входные данные имеют конечную дисперсию 1 .

 

[FXWizard]

Определение проблемы

На некоторое время оставим саму идею оптимального f (мы вернемся к нему позже). Легче всего понять параметрическое выведение эффективной границы, если рассмотреть портфель акций. Будем исходить из того, что эти акции находятся на денежном счете и полностью оплачены, т.е. они куплены не за счет кредита, полученного от брокерской фирмы (не на маржинальном счете). С учетом этого ограничения мы выведем эффективную границу портфелей, т.е. из предложенных акций создадим комбинацию, которая будет иметь наименьший уровень ожидаемого риска для данного уровня ожидаемого выигрыша. Эти уровни задаются степенью неприятия риска инвестором. Теория Марковица (или Современная теория портфеля) часто называется теорией Е— V (Expected return (ожидаемая прибыль) —Variance of return (дисперсия прибыли)). Отметьте, что входные параметры основаны на данных по прибыли, таким образом, входные данные для выведения эффективной границы — это прибыли, которые мы ожидаем по данной акции, и дисперсия, которая ожидается от этих прибылей. Прибыли по акциям определяются как дивиденды, ожидаемые за определенный период времени, плюс повышение рыночной стоимости акций (или минус уменьшение) за этот же период, выраженные в процентах. Рассмотрим четыре потенциальные инвестиции, три из которых — в акции, а одна — в сберегательный счет с процентной ставкой 8 1/2% в год. Отметьте, что в этом примере продолжительность периода инвестирования (когда мы измеряем прибыли и их дисперсии) — 1 год:

1
Для получения дополнительной информации прочитайте Fama, Eugene E, «Portfolio Analysis in a Stable Paretian Market», Management Science 11, pp. 404 — 419, 1965. Фама продемонстрировал параметрические методы поиска эффективной границы для стабильно распределенных ценных бумаг (распределения которых обладают одинаковым характеристическим показателем А), когда прибыли компонентов зависят от одного индекса основного рынка. Существует и другая работа, посвященная выведению эффективной границы в условиях бесконечной дисперсии прибылей компонентов портфеля. Эти методы не рассматриваются в данной книге, но для заинтересованных читателей есть ссылки на соответствующие статьи. О распределении Парето
вы сможете узнать из приложения В. Несколько слов о бесконечной дисперсии сказано в разделе «Распределение Стьюдента» в приложении В.

Если прибавить к значению ожидаемой прибыли единицу, мы получим HPR. Также мы можем извлечь квадратный корень из значения ожидаемой дисперсии прибыли и получить ожидаемое стандартное отклонение прибыли.
Используемый временной горизонт не имеет значения при условии, что он одинаковый для всех рассматриваемых компонентов. Если речь идет о прибыли, неважно, что мы используем: год, квартал, 5 лет или день, — пока ожидаемые прибыли и стандартные отклонения для всех рассматриваемых компонентов имеют одни и те же временные рамки.

Ожидаемая прибыль — это то же самое, что и потенциальная прибыль, а дисперсия (или стандартное отклонение) ожидаемых прибылей ~ то же самое, что и потенциальный риск. Отметьте, что данная модель двумерная. Мы можем сказать, что модель представлена правым верхним квадрантом декартовой системы координат (см. рисунок 6-1), где по вертикали (ось Y) откладывается ожидаемая прибыль, а по горизонтали (ось X) откладывается ожидаемая дисперсия, или стандартное отклонение прибылей.

Рисунок 6-1 Правый верхний квадрант декартовой системы координат

 

[FXWizard]

Есть и другие аспекты потенциального риска, такие как потенциальный риск (вероятность) катастрофического убытка, который теория Е — V не рассматривает отдельно от дисперсии прибылей. Мы не будем изучать эту концепцию в данной главе, а будем обсуждать теорию Е — V в классическом варианте. Марковиц также утверждал, что портфель, полученный из теории Е — V, оптимален только в том случае, если полезность, т.е. «удовлетворение» инвестора, является лишь функцией ожидаемой прибыли и дисперсии ожидаемой прибыли. Марковиц указал, что инвестор может использовать и более высокие моменты распределения, а не только первые два (на которых основана теория Е — V), например асимметрию и эксцесс ожидаемых прибылей.
Потенциальный риск — очень емкое понятие, он является функцией гораздо большего числа переменных и включает более высокие моменты распределений.
Тем не менее мы будем определять потенциальный риск как дисперсию ожидаемых прибылей. Не следует, однако, полагать, что этим риск полностью определен. Риск намного шире, и его реальная природа плохо поддается количественной оценке.
Первое, что должен сделать инвестор, желающий использовать теорию Е — V, это придать количественный смысл своим предположениям относительно ожидаемых прибылей и дисперсий прибылей рассматриваемых ценных бумаг на определенном временном горизонте (периоде удержания). Эти параметры можно получить эмпирически. Инвестор может рассмотреть прошлую историю ценных бумаг и рассчитать прибыли и их дисперсии за определенные периоды. Как уже было отмечено, термин «прибыли» означает не только дивиденды по ценной бумаге, но и любые повышения стоимости ценной бумаги (в процентах).
Дисперсия является статистической дисперсией процентных прибылей. Для определения ожидаемой прибыли в период удержания можно использовать линейную регрессию по прошлым прибылям. Дисперсия как входной параметр определяется путем расчета дисперсии каждой прошлой точки данных на основе ее спрогнозированного значения (а не на основе линии регрессии, рассчитанной для прогнозирования следующей ожидаемой прибыли). Вместо того чтобы определять эти значения эмпирическим способом, инвестор может оценить значения будущих прибылей и дисперсий 1 . Возможно, наилучшим способом нахождения параметров является комбинация обоих подходов. Инвестору следует использовать эмпирический подход (т.е. использовать исторические данные), затем, если это необходимо, можно учесть прогноз относительно будущих значений ожидаемых прибылей и дисперсий. Следующими параметрами, которые должен знать инвестор для использования данного метода, являются коэффициенты линейной корреляции прибылей. Эти параметры можно получить эмпирически, путем оценки или с помощью комбинации обоих подходов.
При определении коэффициентов корреляции важно использовать точки данных того же временного периода, который был использован для определения ожидаемых прибылей и дисперсий. Другими словами, если вы используете годовые данные для определения ожидаемых прибылей и дисперсии прибылей (т.е. ведете расчеты на годовой основе), следует использовать годовые данные и при определении коэффициентов корреляции. Если вы используете дневные данные для определения ожидаемых прибьыей и дисперсии прибылей (т.е. ведете расчеты на дневной основе), тогда вам следует использовать дневные данные для определения коэффициентов корреляции. Вернемся к нашим четырем инвестициям — Toxico, Incubeast Corp., LA Garb и сберегательному счету. Присвоим им символы Т, 1, L и S соответственно. Ниже приведена таблица их коэффициентов линейной корреляции:

1 Расчет дисперсии может оказаться довольно сложным. Более легким способом является расчет среднего абсолютного отклонения, которое следует умножить на 1,25 для получения стандартного отклонения. Если возвести это значение в квадрат, мы получим оценку дисперсии.

На основе полученных параметров мы можем рассчитать ковариацию между двумя ценными бумагами:

Стандартные отклонения S a и S б можно найти, взяв квадратный корень дисперсии ожидаемых прибылей для ценных бумаг а и б. Вернемся к нашему примеру. Мы можем определить ковариацию между Toxico (Т) и Incubeast (I) следующим образом:

Зная ковариацию и стандартные отклонения, мы можем рассчитать коэффициент линейной корреляции:

Отметьте, что ковариация ценной бумаги самой к себе является дисперсией, так как коэффициент линейной корреляции ценной бумаги самой к себе равен 1:

Теперь можно создать таблицу ковариаций для нашего примера с четырьмя инвестиционными альтернативами:

 

[FXWizard]

Мы собрали необходимую параметрическую информацию и теперь попытаемся сформулировать основную проблему. Во-первых, сумма весов ценных бумаг, составляющих портфель, должна быть равна 1, так как операции ведутся на денежном счете, и каждая ценная бумага полностью оплачена:

где N == число ценных бумаг, составляющих портфель;
Х = процентный вес ценной бумаги L
Важно отметить, что в уравнении (6.04) каждое значение Х должно быть неотрицательным числом.
Следующее равенство относится к ожидаемой прибыли всего портфеля — это Е в теории Е — V. Ожидаемая прибыль портфеля является суммой прибылей его компонентов, умноженных на соответствующие веса:

где Е = ожидаемая прибыль портфеля;
N = число ценных бумаг, составляющих портфель;
X i = процентный вес ценной бумаги i;
U i = ожидаемая прибыль ценной бумаги i. И наконец, мы подошли к параметру V, т. е дисперсии ожидаемых прибылей:

Нашей целью является поиск значений Х (причем их сумма равна единице), которые дают наименьшее значение V для определенного значения Е. Максимизировать (или минимизировать) функцию Н(Х, Y) при наличии условия или ограничения G(X, Y) можно с помощью метода Лагранжа. Для этого зададим функцию Лагранжа F(X, Y, L):

(6.07) F(X,Y,L) = H(X,Y) + L * G(X,Y)

Обратите внимание на форму уравнения (6.07). Новая функция F(X,Y,L) равна множителю Лагранжа L (его значение мы пока не знаем), умноженному на ограничительную функцию G(X,Y), плюс первоначальная функция H(X,Y), экстремум которой мы и хотим найти.
Решение этой системы из трех уравнений даст точки (X 1 Y 1 ) относительного экстремума:

F x X,Y,L) = О F y (X,Y,L) = О F L (X,Y,L) = О

Допустим, мы хотим максимизировать произведение двух чисел при условии, что их сумма равна 20. Пусть Х и Y два числа. Таким образом, H(X,Y) = Х * Y является функцией, которая должна быть максимизирована при наличии ограничительной функции G(X,Y) = Х + Y - 20 = 0. Зададим функцию Лагранжа:

F(X,Y,L) = Х * Y + L * (X + Y- 20) F x (X,Y,L)=Y+L F y (X,Y,L)=X+L F L (X,Y,L)= X +Y-20
Теперь приравняем F^(X,Y,L) и Fy(X,Y,L) нулю и решим каждое из них для получения L:

Y+L=0 Y=-L и
X+L=0 X=-L
Теперь, приняв F L (X,Y,L) = 0, мы получим Х + Y - 20 = 0. Наконец, заменим Х и Y эквивалентными выражениями, содержащими L:

(-L) + (-L) - 20 = О 2 * -L - 20 L=-10

Так как Y = -L, то Y = 10 и Х = 10. Максимальное произведение: 10*10= 100.
Метод множителей Лагранжа был продемонстрирован для двух переменных и одной 01раничительной функции. Метод можно также применять, когда есть более чем две переменные и более чем одна ограничительная функция. Далее для примера следует форма для поиска экстремума, когда есть три переменные и две ограничительные функции: