Ральф Винс. Математика управления капиталом

[FXWizard]

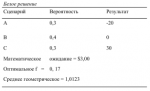
Затем перейдем к следующему сценарию под названием «Кризис» с вероятностью 0,2 проигрыша 200 000 долларов. Наш результат наихудшего случая все еще -$500 000. Значение f, с которым мы работаем, по-прежнему 0,01, поэтому число, на которое надо разделить результат этого сценария, составляет 50 000 000 долларов:

-$200 000/$50 000 000 = -0,004

Проведем дальнейшие вычисления для получения HPR:

1 + (-0,004) = 0,996 0,99^0,2 = 0,9991987169

Если мы рассмотрим остальные сценарии при тестируемом значении f=0,01, то найдем три значения HPR, соответствующие последним 3 сценариям:

Застой 1,0
Мир 1,004487689
Процветание 1,000990622

После того как найдены все HPR для данного значения f, необходимо перемножить полученные HPR:

0,9989954713*0,9991987169*1,0*1,004487689 * 1,000990622=1,003667853

Мы получили промежуточное TWR = 1,003667853. Следующим шагом будет возведение этого значения в степень, равную единице, деленной на сумму вероятностей. Так как сумма вероятностей составляет 1, то, чтобы получить среднее геометрическое, TWR возведем в степень 1. Таким образом, среднее геометрическое равно в этом случае TWR, то есть 1,003667853. Если, однако, убрать ограничение. что каждый сценарий должен иметь уникальную вероятность, то можно получить сумму вероятностей больше 1. В таком случае, чтобы получить среднее геометрическое, надо возвести TWR в степень, равную единице, деленной на эту сумму вероятностей.
Ответ, полученный в нашем примере, является средним геометрическим. соответствующим значению f= 0,01. Теперь перейдем к значению f= 0,02 и повторим весь процесс, пока не найдем среднее геометрическое, соответствующее этому f. Мы будем продолжать, пока не дойдем до такого значения f, которое даст наивысшее среднее геометрическое.
В нашем примере наивысшее среднее геометрическое достигается при f=0,57 и равно 1,1106. Разделив возможный результат наихудшего сценария (-$500 000) на отрицательное оптимальное f, мы получим 877 192,35 доллара. Другими словами, если корпорации АБВ надо разместить на рынке новый продукт в этой далекой стране, следует инвестировать именно эту сумму. С течением времени и развитием событий, когда изменятся возможные исходы и вероятности, изменится также и сумма f. Чем чаще корпорация АБВ будет учитывать эти изменения, тем более правильными будут ее решения. Отметьте. что если корпорация АБВ инвестирует в этот проект меньше 877 192,35 доллара. тогда она находится левее пика кривой f.
Это аналогично ситуации, когда у трейдера открыто слишком мало контрактов (по сравнению с оптимальным f). Если корпорация АБВ вкладывает в проект большую сумму, это аналогично ситуации, когда у трейдера открыто слишком много позиций.
Количество, рассмотренное здесь, является количеством денег, но это могут быть не только деньги, и метод будет работать. Данный подход можно использовать для любого количественного решения в среде благоприятной неопределенности .

 

[FXWizard]

Если вы создадите различные сценарии для фондового рынка, оптимальное f. полученное с помощью этого метода, даст вам процент средств, которые надо в данный момент инвестировать в акции. Например, если f= 0,65, то 65% вашего баланса должно быть на рынке, а оставшиеся 35%, например, в деньгах. Этот подход даст вам наибольший геометрический рост капитала. Конечно, результат будет зависеть от того, какие входные данные вы использовали в системе (сценарии. их вероятности осуществления, выигрыши и проигрыши, издержки). Все сказанное ранее об оптимальном f применимо здесь, и это означает также, что ожидаемые проигрыши могут достигать 100%. Если вы осуществляете планирование сценария для размещения активов, то должны ожидать, что около 100% активов.
размещенных в соответствии с рассматриваемым сценарием, могут быть потеряны в какое-либо время в будущем. Например, вы используете данный метод, чтобы определить сумму средств, предназначенных для инвестирования в акции. Допустим, вы приходите к выводу, что 65% средств должно быть инвестировано в акции, а оставшиеся 35% в безрисковые активы. Следует ожидать, что проигрыш в будущем может достичь 100% суммы, размещенной на фондовом рынке. Другими словами, вы должны быть готовы, что в какой-либо точке в будущем почти 100% активов от ваших 65%, размещенных в акции, будут проиграны. Однако именно таким образом вы достигнете максимального геометрического роста. Ту же процедуру можно использовать для альтернативного параметрического метода определения оптимального f в торговле. Допустим, вы принимаете торговые решения, основываясь на фундаментальных данных. Вы намечаете различные сценарии, которые могут произойти в процессе торговли. Чем больше сценариев и чем точнее сценарии, тем лучше будут полученные результаты. Предположим, вы решили купить муниципальные облигации, но при этом не планируете удерживать их до срока погашения. Вы можете рассмотреть множество сценариев будущих событий и использовать эти сценарии для определения оптимального размера
инвестиций.
Концепцию планирования сценария для определения оптимального f можно использовать во многих областях: от военных стратегий до определения оптимального уровня участия в подписке на акции или оптимальной предоплаты за дом.
Этот метод, вероятно, является лучшим и уже точно самым легким для тех, кто не использует механические решения при входе и выходе с рынка. Трейдеры, которые торгуют по фундаментальным данным, графикам, волнам Эллиотта или с помощью любого другого метода, требующего субъективного суждения, могут найти оптимальные f с помощью этого подхода — он намного проще, чем поиск значений параметров распределения. Арифметическое среднее HPR группы сценариев можно рассчитать следующим образом:

где N = число сценариев;
А = результат (выигрыш или проигрыш) сценария i;
Р = вероятность сценария i;
W= наихудший результат среди всех сценариев.

 

[FXWizard]

AHPR будет важно позднее, при поиске эффективной границы совокупности нескольких рыночных систем, когда необходимо будет определить ожидаемую прибыль (арифметическую) данной рыночной системы. Эта ожидаемая прибыль равна AHPR-1. Рассмотренный метод не обязательно должен быть основан на параметрическом подходе. Возможен и эмпирический подход. Другими словами, мы можем взять отчет о сделках данной рыночной системы и использовать каждую из этих сделок в качестве сценария, который может произойти в будущем.
Величина прибыли или убытка будет выходным результатом данного сценария. В этом случае каждый сценарий (сделка) имеет равную вероятность осуществления — 1/N, где N — общее число сделок (сценариев). В результате мы получим эмпирическое оптимальное f. Когда есть несколько решений на основе нескольких сценариев, выбор того. чье среднее геометрическое, соответствующее оптимальному f, самое большое. максимизирует решение в асимптотическом смысле. Зачастую это будет происходить вопреки общепринятым правилам принятия решения, таким как Правило Гурвица, максимакс, минимакс, минимаксная потеря (minimax regret) и наивысшее математическое ожидание.
Предположим, мы должны выбрать одно их двух возможных решений, которые назовем «белым» и «черным». Белое решение представляет следующие возможные сценарии:

Черное решение представляет следующие сценарии:

Многие выбрали бы белое решение, так как оно имеет большее математическое ожидание. При белом решении вы можете ожидать «в среднем» выигрыш в 3 доллара против выигрыша черного решения в 2,90 доллара. Однако выбор черного решения будет более правильным, так как оно дает наибольшее среднее геометрическое. При черном решении можно ожидать «в среднем» выигрыш в 4,53% (1,0453 - 1) против выигрыша белого решения в 1,23%. При реинвестировании черное решение, в среднем, выиграет в три раза больше, чем белое решение! Вы можете возразить, отметив, что мы не реинвестируем по тому же сценарию каждый раз, и можно добиться большего, если всегда выбирать наивысшее арифметическое математическое ожидание для каждого представленного набора. Мы будем принимать решение, основываясь на большем арифметическом математическом ожидании, только в том случае, если не собираемся реинвестировать вообще. Но так как почти всегда деньги, которыми мы рискуем сегодня, будут снова с риском вложены в будущем, а деньги, выигранные или проигранные в прошлом, влияют на то, чем мы можем рисковать сегодня (среда геометрических следствий), для максимизации долгосрочного роста капитала мы должны принимать решения, исходя из среднего геометрического.
Даже если сценарии, которые будут представлены завтра, не будут такими же, как сегодня, используя наибольшее среднее геометрическое, мы всегда максимизируем наши решения. Это аналогично процессу зависимых попыток, например игре в «очко». Каждая раздача изменяет вероятности, поэтому оптимальная ставка изменяется, чтобы максимизировать долгосрочный рост.
Помните, чтобы максимизировать долгосрочный рост, мы должны рассматривать текущую игру как неограниченную во времени. Другими словами, следует рассматривать каждую отдельную ставку, как будто она повторяется бесконечное число раз, если необходимо максимизировать рост в течение долгой последовательности ставок в нескольких играх. Давайте обобщим все вышесказанное: когда результат события оказывает влияние на результат(ы) последующего события(ий), нам следует выбирать наибольшее геометрическое ожидание. В редких случаях, когда результат не влияет на последующие события, следует выбирать наибольшее арифметическое ожидание. Математическое ожидание (арифметическое) не учитывает зависимость результатов внутри каждого сценария и поэтому может привести к неверному заключению, когда рассматривается реинвестирование в геометрической среде. Использование предложенного метода в планировании сценария поможет вам правильно выбрать сценарий, оценить его результаты и вероятности их осуществления. Этот метод внутренне более консервативен, чем размещение на основе наибольшего арифметического математического ожидания. Уравнение (3.05) показывает, что среднее геометрическое никогда не может быть больше среднего арифметического. Таким образом, этот метод никогда не будет более рискованным, чем метод наибольшего арифметического математического ожидания. В асимптотическом смысле (долгосрочном) это не только лучший метод размещения, так как вы получаете наибольший геометрический рост, он также более безопасен, чем размещение по наибольшему арифметическому математическому ожиданию, которое неизменно смещает вас вправо от пика кривой f.
Так как реинвестирование почти всегда имеет место в реальной жизни (до того дня, когда вы уйдете на пенсию), 1 то есть вы снова будете использовать деньги, которые использовали сегодня, мы должны принимать решения, исходя из того, что такая возможность представится тысячи раз, для того чтобы максимизировать рост. Мы должны принимать решения таким образом, чтобы максимизировать геометрическое ожидание. Более того, так как результаты большинства событий влияют на результаты последующих событий, нам следует принимать решения и размещать средства, основываясь на максимальном геометрическом ожидании, что может привести к решениям, которые не всегда очевидны.

 

[FXWizard]

1 В некоторых случаях лучшим выбором будет именно наибольшее арифметическое математическое ожидание, а не геометрическое. Например, когда трейдер торгует постоянным количеством контрактов и желает перейти к работе «фиксированной долей» в какой-то благоприятной точке в будущем. Эта благоприятная точка — порог геометрической торговли, где арифметическая средняя сделка, которая используется в качестве входного данного, рассчитывается как арифметическое математическое ожидание (сумма результатов каждого сценария, умноженных на вероятность их появления), поделенное на сумму вероятностей всех сценариев. Так как сумма вероятностей всех сценариев обычно равна 1, мы можем говорить, что арифметическая средняя сделка равна арифметическому математическому ожиданию

Поиск оптимального f по ячеистым данным

Теперь мы рассмотрим поиск оптимального f и его побочных продуктов по ячеистым данным. Этот подход также является гибридом параметрического и эмпирического метода и аналогичен процессу поиска оптимального f по различным сценариям; только на этот раз мы будем использовать среднюю точку ячейки. Для каждой ячейки у нас будет ассоциированная вероятность, рассчитанная как общее число элементов (сделок) в этой ячейке, деленное на общее число элементов (сделок) во всех ячейках. Для каждой ячейки у нас будет ассоциированный результат, рассчитанный по центральной точке ячейки.
Например, у нас есть 3 ячейки и 10 сделок. Первую ячейку мы определим для P&L от -1000 долларов до -100 долларов. В этой ячейке будет два элемента. Следующая ячейка предназначена для сделок от -100 до 100 долларов, она вмещает 5 сделок.
Наконец, в третью ячейку попадут 3 сделки, которые имеют P&L от 100 до 1000 долларов.

Теперь нам нужно решить уравнение (4.16), где каждая ячейка представляет отдельный сценарий. Таким образом, для случая с 3 ячейками оптимальное f составляет 0,2, или 1 контракт на каждые 2750 долларов на счете (наш проигрыш наихудшего случая будет средней точкой первой ячейки, или (-$1000 + -$100) / /2 =-$550). Этот метод можно использовать в реальной торговле, хотя он и недостаточно точен, поскольку допускает, что наибольший проигрыш находится в середине наихудшей ячейки, а это не совсем верно. Часто полезно иметь одну
лишнюю ячейку, чтобы включить проигрыш наихудшего случая. Допустим, как и в примере с 3 ячейками, у нас была сделка с проигрышем в 1000 долларов. Такая сделка попадает в ячейку -1000 до -100 долларов и поэтому будет записана как 550 долларов (средняя точка ячейки), но мы можем разместить в ячейки те же данные следующим образом:

Теперь оптимальное f составляет 0,04, или 1 контракт на каждые 25 000 долларов на счете. Вы видите, насколько приблизителен этот метод? Поэтому, хотя этот метод даст нам оптимальное f для ячеистых данных, надо понимать, что потеря информации при размещении данных в ячейки может сделать результаты настолько неточными, что они станут бесполезными. Если бы у нас было больше точек данных и больше ячеек, метод был бы намного точнее. Фактически, если бы у нас было бесконечное количество данных и бесконечное число ячеек, метод был бы абсолютно точным (если бы данные в каждой из ячеек были равны средним точкам соответствующих ячеек, то этот метод также был бы точным). Другой недостаток предлагаемого метода заключается в том, что среднее значение ячейки не обязательно расположено в центре ячейки. В реальности среднее значение элементов в ячейке будет ближе к моде всего распределения, чем к средней точке ячейки. Следовательно, полученная дисперсия будет больше, чем есть на самом деле. Существуют способы корректировки, но и они могут быть неточными.
Проблему можно было бы преодолеть, и результаты были бы точными при бесконечном количестве элементов (сделок) и бесконечном количестве ячеек. Если у вас есть достаточно большое количество сделок и достаточно большое количество ячеек, вы можете использовать этот метод с большей уверенностью.
Вы также можете провести тесты «что если», изменяя число элементов в различных ячейках, чтобы получить более точное приближение.

 

[FXWizard]

Какое оптимальное f лучше?

Мы знаем, что можно найти оптимальное f, используя эмпирический подход, а также используя некоторые параметрические методы как для ячеистых, так и для неячеистых данных. Мы также знаем, что можно привести данные к текущей цене.
Какое оптимальное f действительно оптимально — полученное по приведенным или неприведенным данным?
Неприведенное эмпирическое оптимальное f рассчитывается на прошлых данных. Эмпирический метод для нахождения оптимального f, описанный в главе 1, даст оптимальное f, которое реализовало бы наивысший геометрический рост по прошлому потоку результатов. Однако нам надо определить, какое значение оптимального f использовать в будущем (особенно в следующей сделке), учитывая, что у нас нет достоверной информации об исходе следующей сделки. Мы точно не знаем, будет это прибыль (тогда оптимальное f будет 1) или убыток (тогда оптимальное f будет 0). Мы можем выразить результат следующей сделки только распределением вероятности. Лучшим подходом для трейдеров, применяющих механическую систему, будет расчет f путем использования параметрического метода с помощью регулируемой функции распределения, описанной в этой главе, с приведенными или неприведенными данными. Если есть значительное различие в использовании приведенных данных по сравнению с неприведенными, тогда, вероятно, расчеты сделаны по слишком большой истории сделок, или же данных на уровне текущих цен недостаточно. Для несистемных трейдеров лучшим может оказаться подход планирования сценария.
Теперь вы имеете представление как об эмпирических, так и параметрических методах, а также о некоторых гибридных методах поиска оптимального f. В следующей главе мы рассмотрим проблему поиска оптимального f (параметрическим способом) для случая, когда одновременно открыто несколько позиций.

 

[FXWizard]

Глава 5
Введение в методы управления капиталом с использованием параметрического подхода при одновременной торговле по нескольким позициям

В этой книге уже упоминалось об использовании опционов отдельно или совместно с позицией по базовому инструменту для улучшения торговых результатов. Покупка пут-опциона вместе с длинной позицией по базовому инструменту (или просто покупка колл-опциона), а иногда даже продажа (короткая продажа) колл-опциона совместно с длинной позицией по базовому инструменту могут ускорить асимптотический геометрический рост. Это происходит потому, что очень часто (но не всегда) использование опционов уменьшает дисперсию в большей степени, чем уменьшает арифметический средний доход. В результате, исходя из фундаментального уравнения торговли, мы получаем большее оценочное TWR. Опционы можно использовать как самостоятельные инструменты, так и вместе с позициями по базовому инструменту для управления риском. В будущем, так как трейдеры все больше концентрируются на управлении риском, опционы, вероятно, будут играть еще большую роль. В книге «Формулы управления портфелем» была рассмотрена взаимосвязь оптимального/и опционов. * В этой главе мы продолжим начатую дискуссию и обсудим торговлю по нескольким позициям, а также поговорим об опционах. Настоящая глава посвящена еще одному методу поиска оптимального/для немеханических торговых систем. Параметрические методы, рассмотренные до этого момента, могут использовать те, кто не применяет механические системы. Допустим, вы не используете механическую систему и применяете метод, описанный в главе 4. Если вы захотите рассчитать эксцесс, то сделать это будет не очень легко (по крайней мере, точное значение эксцесса быстро получить, скорее всего, не удастся). Данная глава предназначена прежде всего для тех, кто использует немеханические методы принятия решений об открытии и закрытии позиций. Трейдерам, использующим эти методы, надо будет рассчитывать не параметры распределения сделок, а значения для волатильности базового инструмента и прогнозируемой цены базового инструмента. Трейдеру, не использующему механическую, объективную систему, будет намного легче получить именно эти величины, чем рассчитать параметры для распределения сделок, которые еще не произошли.
Обсуждение оптимального/и его побочных продуктов для тех трейдеров, которые не используют механическую, объективную систему, мы начнем с рассмотрения ситуации, когда одновременно открыто несколько позиций.
Означает ли это, что тот, кто использует механические методы для открытия и закрытия позиций, не может использовать описанные подходы? Нет. В Главе 6 предложен метод поиска оптимальных, одновременно открытых позиций независимо от того, использует трейдер механическую систему или нет. В этой главе рассмотрена ситуация, когда одновременно открыто несколько позиций (с использованием опционов или без), и применяется немеханический подход.

 

[FXWizard]

Расчет волатильности

Один из важных параметров, который трейдер, желающий использовать описываемые в этой главе концепции, должен ввести, — это волатильность. Существует два способа определения волатильности. Первый — использование оценки на основе рыночных данных — дает подразумеваемую волатильность.
Модели ценообразования опционов, представленные в этой главе, используют волатильность в качестве одного из своих входных параметров для получения справедливой теоретической цены опциона. Подразумеваемая волатильность основывается на предположении, что рыночная цена опциона эквивалентна его справедливой теоретической цене. Волатильность, которая дает справедливую теоретическую цену, равную рыночной цене, и есть подразумеваемая волатильность. Второй метод расчета волатильности основывается на использовании исторических данных. Полученная таким образом историческая волатильность определяется фактической ценой базового инструмента. Хотя волатильность в качестве входного данного в модели ценообразования опционов выражается в годовых процентах, при ее определении используется более короткий временной отрезок, обычно 10-20 дней, а получившийся в результате ответ переводится в годовое значение.
Ниже показан расчет 20-дневной годовой исторической волатильности.
Шаг 1. Разделите сегодняшнее закрытие на предыдущее закрытие рыночного дня.
Шаг 2. Возьмите натуральный логарифм частного, полученного в шаге 1. Для примера рассчитаем годовую историческую волатильность японской йены на март 1991 года. При написании даты будем использовать формат (год/месяц/день). Закрытие 910225, равное 74,52, разделим на закрытие 910222, равное 75,52.
74,82 / 75,52 = 0,9907309322 Натуральный логарифм 0,9907309322 равен 0,009312258.
Шаг 3. По истечении 21 дня у вас будет 20 значений для шага 2. Теперь рассчитайте 20-дневную скользящую среднюю значений из шага 2.
Шаг 4. Найдите 20-дневную дисперсию выборки данных из шага 2. Для этого необходима 20-дневная скользящая средняя (см. шаг 3). Далее, для каждого из 20 последних дней вычтем скользящую среднюю из значений шага 2.
Теперь возведем в квадрат полученные значения, чтобы преобразовать все отрицательные ответы в положительные. После этого сложим все значения за последние 20 дней. Наконец, разделим найденную сумму на 19 и получим дисперсию по выборке данных за последние 20 дней. 20-дневная дисперсия для 901226 составляет 0,00009. Подобным образом вы можете рассчитать 20-дневную дисперсию для любого дня.
Шаг 5. После того как вы определили 20-дневную дисперсию для конкретного дня, необходимо преобразовать ее в 20-дневное стандартное отклонение. Это легко сделать путем извлечения квадратного корня из дисперсии. Таким образом, для 901226 квадратный корень дисперсии (которая, как было показано, равна 0,00009) даст нам 20-дневное стандартное отклонение 0,009486832981.
Шаг 6. Теперь преобразуем полученные данные в «годовые». Так как мы используем дневные данные и исходим из того, что по йене в году 252 торговых дня (примерно), умножим ответы из шага 5 на квадратный корень 252, то есть на 15,87450787. Для 901226 20-дневное стандартное отклонение по выборке составляет 0,009486832981. Умножив его на 15,87450787, получаем 0,1505988048. Это значение является исторической волатильностью, в нашем случае — 15,06%, и оно может быть использовано в качестве входного значения волатильности в модели ценообразования опционов Блэка-Шоулса.
Следующая таблица показывает шаги, необходимые для нахождения 20-дневной «годовой» исторической волатильности. Заметьте, что промежуточные шаги для определения дисперсии, которые были показаны в предыдущей таблице, сюда не включены.

торгуете без опционов и рассматриваете торговлю как не ограниченную во времени, ваш реальный риск банкротства равен 1. При таких условиях вы неминуемо разоритесь, что вполне согласуется с уравнениями риска банкротства, поскольку в них в качестве входных переменных используются эмпирические данные, то есть входные данные в уравнениях риска банкротства основываются на ограниченных наборах сделок. Утверждение о гарантированном банкротстве при бесконечно долгой игре с неограниченной ответственностью делается с позиций параметрического подхода. Параметрический подход учитывает большие проигрышные сделки, которые расположены в левом хвосте распределения, но еще не произошли, поэтому они не являются частью ограниченного набора, используемого в качестве входных данных в уравнениях риска банкротства. Для примера представьте себе торговую систему, в которой применяется постоянное количество контрактов. В каждой сделке используется 1 контракт. Чтобы узнать, каким может стать баланс через Х сделок, мы просто умножим Х на среднюю сделку. Таким образом, если система имеет среднюю сделку 250 долларов и мы хотим знать, каким может стать баланс через 7 сделок, мы $250 умножим на 7 и получим $1750. Отметьте, что кривая арифметического математического ожидания задается линейной функцией. Любая сделка может принести убыток, который отбросит нас назад (временно) от ожидаемой линии. В такой ситуации есть предел проигрыша по сделке. Так как наша линия всегда выше, чем самая большая сумма, которую можно проиграть за сделку, мы не можем обанкротиться сразу. Однако длинная проигрышная полоса может отбросить нас достаточно далеко от этой линии, и мы не сможем продолжить торговлю, то есть обанкротимся. Вероятность подобного развития событий уменьшается с течением времени, когда линия ожидания становится выше. Уравнение риска банкротства позволяет рассчитать вероятность банкротства еще до того, как мы начнем торговать по выбранной системе. Если бы мы торговали в такой системе на основе фиксированной доли счета, линия загибалась бы вверх, становясь после каждой сделки все круче. Однако проигрыш всегда сопоставим с тем, насколько высоко мы находимся на линии. Таким образом, вероятность банкротства не уменьшается с течением времени. В теории, однако, риск банкротства при торговле фиксированной долей счета можно сделать равным нулю, если торговать бесконечно делимыми единицами. К реальной торговле это не применимо. Риск банкротства при торговле фиксированной долей счета всегда немного выше, чем в этой же системе при торговле на основе постоянного количества контрактов. В действительности, нет верхнего предела суммы, которую вы можете проиграть за одну сделку; кривые состояния счета могут снизиться до нуля за одну сделку независимо от того, насколько высоко они расположены. Таким образом, если мы торгуем бесконечно долгий период времени инструментом с неограниченной ответственностью, постоянным количеством контрактов или фиксированной долей счета, риск банкротства составляет 1. Банкротство гарантировано. Единственный способ избежать такого развития событий — поставить ограничение на максимальный проигрыш. Этого можно достичь, используя опционы, когда позиция относится в дебет (если трейдер платит за премию больше, чем получает, то разница между уплаченной и полученной суммами называется «дебет») 1 .

1 Позднее в этой главе мы увидим, что базовые инструменты идентичны колл-опционам с неограниченным сроком истечения. Поэтому, если у нас открыта длинная позиция по базовому инструменту, мы можем сказать, что проигрыш наихудшего случая является полной стоимостью инструмента. В большинстве случаев проигрыш такой величины и является катастрофическим проигрышем. Короткая позиция по базовому инструменту аналогична короткой позиции по колл-опциону с неограниченным сроком истечения, и в такой ситуации ответственность действительно не ограничена.

 

[FXWizard]

Модели ценообразования опционов

Представьте себе базовый инструмент (акция, облигация, валюта, товар и т.д.), цена которого движется вверх или вниз на 1 тик каждую последующую сделку
Если мы будем измерять возможную стоимость акции через 100 тиков и рассмотрим большое количество вариантов, то обнаружим, что полученное распределение результатов — нормальное. Поведение цены в данном случае будет напоминать падение шарика через доску Галтона. Если рассчитать цену опциона, исходя из того принципа, что прибыль при покупке или продаже опционов должна быть равна нулю, мы получим биномиальную модель ценообразования опционов (или, коротко, биномиальную модель). Ее иногда также называют моделью Кокса-Росса-Рубинштейна в честь ее разработчиков. Такая цена опциона основывается на его ожидаемой стоимости (его арифметическом математическом ожидании), с тем расчетом, что вы не получаете прибыль, покупая или продавая опцион и удерживая его до истечения срока. В этом случае говорят, что опцион справедливо оценен.
Мы не будем углубляться в математику биномиальной модели, а рассмотрим модель фондовых опционов Блэка-Шоулса и модель опционов на фьючерсы Блэка. Вам следует знать, что кроме вышеперечисленных трех моделей есть другие действующие модели ценообразования опционов, которые мы не будут рассматривать, хотя концепции, описанные в этой главе, применимы ко всем моделям ценообразования опционов. Для более подробного изучения математической основы моделей я могу порекомендовать книгу Шелдона Нейтенберга (Volatility and Pricing Strategies by Sheldon Natenberg). Математика модели фондовых опционов Блэка-Шоулса и модели опционов на фьючерсы Блэка, которые мы будем рассматривать, взята из книги Нейтенберга. Тем читателям, которые желают больше узнать о концепции оптимального f и опционах, я советую прочитать фундаментальный труд Нейтенберга.
Давайте обсудим модель ценообразования фондовых опционов Блэка-Шоулса (далее Блэк-Шоулс). Модель названа в честь ее создателей: Фишера Блэка из Чикагского университета и Мирона Шоулса из M.I.T; впервые она была описана в 1973 году (May — June 1973 Journal of Political Economy). Блэк-Шоулс считается предельной формой биномиальной модели. В биномиальной модели нужно задать число тиков, определяющее движение вверх или вниз, прежде чем будет зафиксировано возможное значение цены. Далее следует небольшая диаграмма, которая поясняет эту мысль.

1 Позднее в этой главе мы увидим, что базовые инструменты идентичны колл-опционам с неограниченным сроком истечения. Поэтому, если у нас открыта длинная позиция по базовому инструменту, мы можем сказать, что проигрыш наихудшего случая является полной стоимостью инструмента. В большинстве случаев проигрыш такой величины и является катастрофическим проигрышем. Короткая позиция по базовому инструменту аналогична короткой позиции по колл-опциону с неограниченным сроком истечения, и в такой ситуации ответственность действительно не ограничена.

Текущая цена на первом шаге может пойти в 2-х направлениях. На втором шаге в 4-х направлениях. В биномиальной модели для расчета справедливой цены опциона вы должны заранее определить, сколько всего периодов использовать. Блэк-Шоулс считается предельной формой биномиальной модели, так как допускает бесконечное число периодов (в теории), то есть Блэк-Шоулс подразумевает, что эта небольшая диаграмма будет расширяться до бесконечности. Если вы определите справедливую цену опциона по Блэку-Шоулсу, то получите тот же ответ, что и в случае с биномиальной моделью, если число периодов, используемых в биномиальной модели, будет стремиться к бесконечности. (Тот факт, что Блэк-Шоулс является предельной формой биномиальной модели, подразумевает, что биномиальная модель появилась первой, но на самом деле сначала появилась именно модель Блэка-Шоулса). Справедливая стоимость фондового колл-опциона по Блэку-Шоулсу рассчитывается следующим образом:

а пут-опциона:

где С = справедливая стоимость колл-опциона;
Р = справедливая стоимость пут-опциона;
U = цена базового инструмента;
Е = цена исполнения опциона;
Т = доля года, оставшаяся до истечения срока исполнения выраженная десятичной дробью 1 ;
V= годовая волатильность в процентах;
R = безрисковая ставка;
1п() = функция натурального логарифма;
N() = кумулятивная нормальная функция распределения вероятностей, задаваемая уравнением (3.21).

 

[FXWizard]

Для акций, по которым выплачиваются дивиденды, необходимо скорректировать переменную U и отразить текущую цену базового инструмента с учетом стоимости ожидаемых дивидендов:

где Ц = ожидаемая выплата дивиденда 1;
W. = время (доля года, выраженная десятичной дробью) до выплаты L
Модель Блэка-Шоулса позволяет точно рассчитать дельту, то есть первую производную цены опциона. Это мгновенная скорость изменения опциона по отношению к изменению U (цены базового инструмента):

(5.05) Дельта колл-опциона = N(H)

(5.06) Дельта пут-опциона = -N(-H)

1 Чаще всего только рыночные дни используются при расчете этой переменной. Число рабочих дней в году (григорианское) можно определить следующим образом: 365,2424 / 7*5= 260,8875. Из-за выходных реальное число торговых дней в году обычно составляет от 250 до 252. Поэтому, если мы используем 252-дневный год и осталось 50 торговых дней до истечения
срока, то доля года, выраженная десятичной дробью, т.е. Т, будет 50 / /252=0,1984126984

Эти коэффициенты будут очень важны в Главе 7, когда мы будем рассматривать страхование портфеля.
.
Блэк сделал модель применимой к опционам на фьючерсы, механизм операций с которыми аналогичен операциям с акциями 1 . Модель ценообразования опционов на фьючерсы Блэка аналогична модели фондовых опционов Блэка-Шоулса за исключением переменной Н:

При использовании модели для фьючерсов коэффициент дельта рассчитывается следующим образом:

(5.08) Дельта колл-опциона = EXP(-R * Т) * N(H)
(5.09) Дельта пут-опциона = -EXP(-R * Т) * N(-H)

Для примера рассмотрим опцион, который имеет цену исполнения 600. Текущая рыночная цена базового инструмента равна 575, а годовая волатильность составляет 25%. Мы будем использовать модель опционов на фьючерсы, 252дневный год и безрисковую ставку 0%. Далее мы допустим, что дата истечения опциона — 15 сентября 1991 года (910915), а текущая дата — 1 августа 1991 года (910801).
Сначала рассчитаем переменную Т, а затем преобразуем 910801 и 910915 в их юлианские эквиваленты. Для этого мы должны использовать следующий алгоритм.

 

[FXWizard]

1. Задайте переменные 1, 2 и 3, которые будут определять год, месяц и день, соответственно. Для нашего примера — это 1991, 8 и 1.
2. Если переменная 2 меньше 3 (январь или февраль), тогда переменная 1 будет равна значению года минус 1, а переменная 2 будет равна значению месяца плюс 13.
3. Если значение переменной 2 больше, чем 2 (март или дальше), тогда переменная 2 будет равна значению месяца плюс 1.
4. Задайте переменную 4, которая будет рассчитываться следующим образом:

5. Задайте переменную 5, которая будет равна целой части произведения числа 0,01 и переменной 1:
Математически:
V5=INT(0,01*V1)
6. Рассчитаем юлианскую дату:

1
При торговле фьючерсами не требуется немедленной уплаты денежных средств за базовый актив, хотя необходимо уплатить залог. Кроме того, все прибыли и убытки реализуются немедленно, даже когда позиция не ликвидирована. Эти пункты находятся в прямом противоречии с механизмом сделок по акциям. При торговле акциями покупка требует полной и немедленной оплаты, а прибыли (или убытки) не реализуются, пока позиция не ликвидирована.

Юлианская дата = V4 + 2 - V5 + INT(0,25 * V5) Преобразуем дату 910901 в юлианскую:
Шаг 1. VI = 1991, V2 = 8, V3 = 1.
Шаг 2. Так как наш месяц в этом примере идет за январем и февралем, то этот шаг не применяется.
Шаг 3. Так как этот месяц идет за январем и февралем, то получим:
V2 = 8 + 1 = 9. Шаг 4. Теперь найдем V4:
V4 = V3 + 1 720 995 + INT(365,25 * VI) + INT(30,6001 * V2) = 1 + 1 720 995 + INT(365,25 * 1991) + INT(30,6001 * 9) = 1 + 1 720 995 + INT(727 212,75) + INT(275,4009) =1+1720 995 + 727 212 + 275 = 2 448 483 Шаг 5. Далее найдем V5:
V5=INT(0,01*V1) =INT(0,01*1991) = INT(19,91) = 19 Шаг 6. Теперь получим юлианскую дату:
Юлианская дата = V4 + 2 - V5 + INT(0,25 * V5)
= 2 448 483 + 2 - 19 + INT(0,25 * 19) = 2 448 483 + 2 - 19 + INT(4,75) = 2 448 483 + 2 - 19 + 4 = 2 448 470
Таким образом, юлианская дата 1 августа 1991 года равна 2448470. Если мы преобразуем дату истечения опциона 15 сентября 1991 года в юлианскую, то получим 2448515. Если использовать 365-дневный год (или точнее 365,2425-дневный по григорианскому календарю), то, чтобы найти время, оставшееся до истечения срока, необходимо рассчитать разность между двумя юлианскими датами, затем вычесть единицу и полученное значение разделить на 365 (или 365,2425). Однако мы будем использовать не 365-дневный год, а 252-дневный, чтобы учесть только те дни, когда открыта биржа (будние дни минус праздники).
Просмотрим каждый день между двумя юлианскими датами, чтобы понять, является он рабочим днем или нет. Мы можем определить, каким днем недели является юлианская дата, прибавив к ее значению единицу, разделив на 7 и взяв остаток. Остаток будет значением от 0 до 6, соответствуя дню недели от воскресенья до субботы. Таким образом, для 1 августа 1991 года, когда юлианская дата равна 2448470:

День недели = ((2 448 470 + 1) / 7) % 7 =2448471/% 7 = ((2 448 471/7) - INT(2 448 471 / 7)) * 7 =(349 781,5714-349 781)* 7 =0,5714*7 =4

Так как 4 соответствует четвергу, мы можем утверждать, что 1 августа 1991 года является четвергом.
Теперь просмотрим все дни до даты истечения срока опциона. Если мы учтем все рабочие дни между этими двумя датами, то придем к выводу, что между (и включая) 1 августа 1991 года и 15 сентября 1991 года 32 рабочих дня. Из полученного значения следует вычесть единицу, так как мы считаем первым днем 2 августа 1991 года. Таким образом, между 910801 и 910915 31 рабочий день. Теперь мы должны вычесть праздники, когда биржа закрыта. В США 2 сентября 1991 года является Днем Труда. Даже если вы живете в другой стране, биржа, где идет торговля по этому опциону, может находиться в США, и 2 сентября она будет закрыта, поэтому мы вычтем 1 из последнего результата. Таким образом, мы получим 30 торговых дней до истечения срока опциона. Разделим количество торговых дней до истечения срока на число дней в году. Так как мы используем 252-дневный год, то 30/252=0,119047619. Это и есть доля года, выраженная десятичной дробью, т.е. переменная Т.

 

[FXWizard]

Определим переменную Н, необходимую для модели ценообразования. Так как мы используем модель для фьючерсов, то должны рассчитать Н по формуле (5.07):

Уравнение (3.21) для расчета N используется два раза. Первый раз, когда мы находим N(H), второй, когда находим N(H - V * Т^(1/2)). Мы знаем, что V * Т ^ (1/2) = 0,0862581949, поэтому Н - V* Т ^ (1/2) = -0,4502688281 - - 0,0862581949 = -0,536527023. Таким образом, мы должны использовать уравнение (3.21) со следующими вводными значениями переменной Z:
-0,4502688281 и-0,536527023. Из уравнения (3.21) получим 0,3262583 и 0,2957971 соответственно (уравнение (3.21) описано в главе 3, поэтому мы не будем повторять его здесь). Отметьте, что сейчас мы получили коэффициент дельта, мгновенную скорость изменения цены опциона по отношению к изменению цены базового инструмента. Таким образом, дельта для этого опциона составляет 0,3262583. Теперь у нас есть все входные данные, необходимые для определения теоретической цены опциона. Подставив полученные значения в уравнение (5.01), получим:

Таким образом, в соответствии с моделью Блэка для фьючерсов справедливая стоимость колл-опциона с ценой исполнения 600, сроком исполнения 15 сентября 1991 года, при цене базового инструмента на 1 августа 1991 года 575, при волатильности 25%, с учетом 252-дневного года и R = 0 составляет 10,1202625.
Интересно отметить связь между опционами и базовыми инструментами, используя вышеперечисленные модели ценообразования. Мы знаем, что 0 является наименьшей ценой опциона, но верхняя цена — это цена самого базового инструмента. Модели демонстрируют, что теоретическая справедливая цена опциона приближается к верхнему значению (стоимости базового инструмента U) при росте любой или всех трех переменных Т, R или V Это означает, что если мы, например, увеличим Т (время до срока истечения опциона) до бесконечно большого значения, тогда цена опциона будет равна цене базового инструмента. В этой связи мы можем сказать, что все базовые инструменты в действительности эквивалентны опционам с бесконечным Т. Таким образом, все сказанное верно не только для опционов, но и для базовых инструментов, как будто они являются опционами с бесконечным Т. Модель фондовых опционов Блэка-Шоулса и модель опционов на фьючерсы Блэка построены на определенных допущениях.
Разработчики этих моделей исходили из трех утверждений. Несмотря на недостатки этих утверждений, предложенные модели все-таки довольно точны, и цены опционов будут стремиться к значениям, полученным из моделей. Первое из этих утверждений состоит в том, что опцион не может быть исполнен до истечения срока. Это приводит к недооценке опционов американского типа, которые могут исполняться до истечения срока. Второе утверждение предполагает, что мы знаем будущую волатильность базового инструмента, и она будет оставаться постоянной в течение срока действия опциона. На самом деле это не так (т.е. волатильность изменится). Кроме того, распределение изменений волатильности логарифмически нормально, и эту проблему модели не учитывают 1 .
Еще одно допущение модели состоит в том, что безрисковая процентная ставка остается постоянной в течение времени действия опциона. Это также не обязательно. Более того, краткосрочные ставки логарифмически нормально распределены. То обстоятельство, что, чем выше краткосрочные ставки, тем выше будут цены опционов, и утверждение относительно неизменности краткосрочных ставок может привести к еще большей недооценке опциона по отношению к ожидаемой цене (его правильному арифметическому математическому ожиданию). Еще одно утверждение (возможно наиболее важное), которое может привести к недооценке стоимости опциона, рассчитанной с помощью модели, по отношению к действительно ожидаемой стоимости, состоит в том, что логарифмы изменений цены распределяются нормально. Если бы опционы характеризовались не числом дней до даты истечения срока, а числом тиков вверх или вниз до истечения, а цена за один раз могла бы изменяться только на 1 тик и он был бы статистически независим от предыдущего тика, то мы могли бы допустить существование нормального распределения. В нашем случае логарифмы изменений цены не имеют таких характеристик. Тем не менее теоретические справедливые цены, полученные с помощью моделей, используются профессионалами на рынке. Даже если некоторые трейдеры применяют модели, которые отличаются от показанных здесь, большинство из них дадут похожие теоретические справедливые цены. Когда реальные цены расходятся с теоретическими до такой степени, что спекулянты могут получить прибыль, цены начинают снова сходиться к так называемой «теоретической справедливой цене». Тот факт, что мы можем спрог-нозировать с достаточной степенью точности, какой будет цена опциона при наличии различных входных данных (время истечения, цена базового инструмента и т.д.), позволяет нам произвести расчеты оптимального f и его побочных продуктов по опционам и смешанным позициям. Читатель должен помнить, что все эти методы основаны на утверждениях, которые только что были изложены.

1 Тот факт, что распределение изменений волатильности логарифмически нормально, не так часто принимается во внимание. Чрезвычайная чувствительность цен опционов к волатильности базового инструмента делает покупку опциона (пут-опциона или колл-опциона) еще более привлекательной в смысле математического ожидания.

 

[FXWizard]

Модель ценообразования европейских опционов для всех распределений

Мы можем создать собственную модель ценообразования, лишенную каких-либо предположений относительно распределения изменений цены.
Сначала необходимо определить термин «теоретически справедливый», относящийся к цене опционов. Мы будем говорить, что опцион справедливо оценен, если арифметическое математическое ожидание цены опциона к моменту истечения, выраженное на основе его текущей стоимости, не принимает во внимание возможного направленного движения цены базового инструмента.
Смысл определения таков: «Какова стоимость данного опциона для меня сегодня как для покупателя опционов»?
Математическое ожидание (арифметическое) определяется из уравнения (1.03):

где р i = вероятность выигрыша или проигрыша попытки i;
a i = выигранная или проигранная сумма попытки i;
N =количество возможных исходов (попыток).
Математическое ожидание представляет собой сумму произведений каждого возможного выигрыша или проигрыша и вероятности этого выигрыша или проигрыша. Когда сумма вероятностей р i больше 1, уравнение 1.03 необходимо разделить на сумму вероятностей р i .
Рассмотрим все дискретные изменения цены, которые имеют вероятность
осуществления, большую или равную 0,001 в течение срока действия контракта, и по ним определим арифметическое математическое ожидание.

где С = справедливая с теоретической точки зрения стоимость опциона, или арифметическое математическое ожидание;
р i = вероятность цены i по истечении срока опциона;
а i = внутренняя стоимость опциона (для кол-опциона: рыночная цена инструмента минус цена исполнения опциона;
для пут-опциона: цена исполнения минус рыночная цена инструмента),
соответствующая базовому инструменту при цене i.
Использование этой модели подразумевает, что, начиная с текущей цены, мы будем двигаться вверх по 1 тику, суммируя значения как в числителе, так и в знаменателе до тех пор, пока вероятность i-ой цены (т.е. р.) не будет меньше 0,001 (вы можете использовать меньшее число, но я считаю, что 0,001 вполне достаточно).
Затем, начиная со значения, которое на 1 тик ниже текущей цены, мы будем двигаться вниз по 1 тику, суммируя значения как в числителе, так и в знаменателе, пока вероятность i-ой цены (т.е. р i ) не будет меньше 0,001. Отметьте, что вероятности, которые мы используем, являются 1-хвостыми, т.е., если вероятность больше чем 0,5, мы вычитаем это значение из 1. Интересно отметить, что значениявероятности р i можно менять в зависимости от того, какое распределение применяется, и оно не обязательно должно быть нормальным, то есть пользовательможет получить теоретическую справедливую цену опциона для любой формы распределения! Таким образом, эта модель дает возможность использовать устойчивое распределение Парето, t-распределение, распределение Пуассона, собственное регулируемое распределение или любое другое распределение, с которым, по нашему мнению, согласовывается цена при определении справедливой стоимости опционов.
Необходимо изменить модель таким образом, чтобы она выражала арифметическое математическое ожидание на дату истечения срока опциона как следующую величину:

где С = справедливая с теоретической точки зрения стоимость опциона, или текущее значение арифметического математического ожидания при данном значении Т;
p i = вероятность цены i по истечении срока опциона;
а i =внутренняя стоимость опциона, соответствующая базовому инструменту при цене i;
R = текущая безрисковая ставка;
Т = доля года, оставшаяся до истечения срока исполнения, выраженная десятичной дробью.

Уравнение (5.11) является моделью ценообразования опционов для всех распределений и дает текущее значение арифметического математического ожидания опциона на дату истечения 1 . Отметьте, что модель можно использовать и для пут-опционов, имея в виду, что значения а. при каждом приросте цены i будут другими. Когда необходимо учесть дивиденды, используйте уравнение (5.04) для корректировки текущей цены базового инструмента. При определении вероятности цены i на дату истечения используйте именно эту измененную текущую цену. Далее следует пример использования уравнения (5.11). Допустим, мы обнаружили, что приемлемой моделью, описывающей распределение логарифмов изменений цены товара, опционы на который мы хотим купить, является распределение Стьюдента 2 . Для определения оптимального числа степеней свободы распределения Стьюдента мы использовали тест К-С и пришли к выводу,
что наилучшее значение равно 5. Допустим, мы хотим определить справедливую цену колл-опциона на 911104 (дата истечения срока опциона — 911220).

 

[FXWizard]

1 Уравнение (5.11) не учитывает разницу между фондовыми опционами и товарными опционами. Согласно общепринятому подходу, в цену фондового опциона включается доход по простой бескупонной облигации, которая будет погашена в момент истечения срока опциона и номинал которой равен цене исполнения. Опционы на товарные фьючерсы, как
считается, имеют процентную ставку 0. Мы же не учитываем это обстоятельство. Если ценная бумага и товар имеют абсолютно одинаковое распределение ожидаемых результатов, т.е. их арифметические математические ожидания равны, то разумный инвестор выберет более дешевый инструмент. Эту ситуацию хорошо иллюстрирует пример, когда вы рассматриваете покупку одного из двух одинаковых домов, и один из них оценен выше только потому, что продавец платил более высокую процентную ставку по ипотечному кредиту

2 Распределение Стьюдента далеко не лучшая модель, описывающая распределение изменений цены. Однако,так как единственным параметром, кроме волатильности (годового стандартного отклонения), который необходимо рассматривать при использовании распределения Стьюдента, является число степеней свободы, а ассоциированные вероятности легко находятся (см. приложение В), мы будем использовать распределение Стьюдента для наглядности.

Цена базового инструмента равна 100, цена исполнения опциона также равна 100. Предположим, годовая волатильность составляет 20%, безрисковая ставка 5% и год равен 260,8875 дням (мы не учитываем праздники, которые выпадают на рабочий день, например День Благодарения в США). Далее допустим, что минимальный тик по этому предполагаемому товару равен 0,10. Используя уравнения (5.01), (5.02) и (5.07) для переменной Н, мы найдем, что справедливая цена равна 2,861 как для колл-опциона, так и для пут-опциона с ценой исполнения 100. Таким образом, эти цены опционов являются справедливыми ценами в соответствии с моделью товарных опционов Блэка, которая допускает логарифмически нормальное распределение цен. Если мы будем использовать уравнение (5.11), то должны сначала рассчитать значения pg. Их можно получить из фрагмента программы, написанной на языке Бейсик и представленной в приложении В. Отметьте, что необходимо знать стандартное значение, т.е. переменную Z, и число степеней свободы, т.е. переменную DEGFDM. Прежде чем мы обратимся к этой программе, преобразуем цену i в стандартное значение по следующей формуле:

где i = цена, соответствующая текущему состоянию процесса суммирования;
V = годовая волатильность, выраженная стандартным отклонением;
Т = доля года, оставшаяся до истечения срока исполнения, выраженная десятичной дробью;
1п() = функция натурального логарифма.
Уравнение (5.12), написанное на БЕЙСИКе, будет выглядеть следующим образом:

Переменная U представляет собой текущую цену базового инструмента (с учетом дивидендов, если это необходимо). Вероятность для распределения Стьюдента, найденная с помощью программы из приложения В, является 2-хвостой. Нам надо сделать ее 1-хвостой и выразить как вероятность отклонения от текущей цены (то есть ограничить ее 0 и 0,5). Это можно сделать с помощью двух строк на БЕЙСИКе:

Таким образом, для 5 степеней свободы справедливая цена колл-опциона равна 3,842, а справедливая цена пут-опциона равна 2,562. Эти величины отличаются от значений, полученных с помощью более традиционных моделей. Причин здесь несколько.
Во-первых, более толстые хвосты распределения Стьюдента с 5 степенями свободы дадут более высокую справедливую стоимость колл-опциона. Вообще, чем толще хвосты распределения, тем больше получается цена колл-опциона. Если бы мы использовали 4 степени свободы, то получили бы еще большую цену колл-опциона.
Стоимость пут-опциона и стоимость колл-опциона значительно отличаются, в то время как в традиционных моделях стоимость пут-опциона и колл-опциона эквивалентна. Этот момент требует некоторого пояснения.

 

[FXWizard]

Справедливую стоимость пут-опциона можно найти из цены колл-опциона с той же ценой исполнения и датой истечения (или наоборот) по формуле пут-колл паритета:

где Р = справедливая цена пут-опциона;
С = справедливая цена колл-опциона;
Е = цена исполнения;
U = текущая цена базового инструмента;
R = безрисковая ставка;
Т = доля года, оставшаяся до истечения срока исполнения, выраженная десятичной дробью.

Когда равенство (5.13) не выполняется, появляется возможность арбитража. Из (5.13) мы видим, что цены, полученные из традиционных моделей, эквивалентны, когда Е - U = 0.
Давайте заменим переменную U в уравнении (5.13) ожидаемой ценой базового инструмента на дату истечения срока опциона. Ожидаемая стоимость базового инструмента может быть определена с помощью уравнения (5.10) с учетом того, что в этом случае а. просто равно i. В нашем примере с DEGFDM = 5 ожидаемая стоимость базового инструмента равна 101,288467. Это происходит потому, что минимальная цена инструмента равна 0, в то время как ограничения цены сверху не существует. Движение цены со 100 до 50 так же вероятно, как и движение со 100 до 200. Следовательно, стоимость колл-опционов будет выше, чем стоимость пут-опционов. Неудивительно, что ожидаемая стоимость базового инструмента на дату истечения должна быть больше, чем его текущая цена, — это вполне согласуется с предположением об инфляции. Когда в уравнении (5.13) мы заменим значение U (текущую цену базового инструмента) на значение ожидаемой стоимости на дату истечения, мы сможем рассчитать справедливую стоимость пут-опциона:
Р = 3,842 + (100 - 101,288467) * ЕХР(-0,05 * 33/260,8875) = 3,842+-1,288467 *ЕХР(- 0,006324565186) = 3,842 + -1,288467 * 0,9936954 = 3,842 + 1,280343731 =2,561656269
Это значение согласуется со стоимостью пут-опциона, полученной из уравнения (5.11).
Остается одна проблема: если пут-опционы и колл-опционы с одной ценой исполнения и сроком истечения оценены согласно уравнению (5.11), тогда существует возможность арбитража. На самом деле LJ в (5.13) является текущей ценой базового инструмента, а не ожидаемым значением базового инструмента на дату истечения. Другими словами, если текущая цена равна 100 и декабрьский коллопцион с ценой исполнения, равной 100, стоит 3,842, а пут-опцион с ценой исполнения, равной 100, стоит 2,561656269, то существует возможность арбитража, исходя из (5.13).
Отсутствие паритета «пут-колл» при наличии наших заново полученных цен опционов предполагает, что вместо покупки колл-опциона за 3,842 нам следует открыть эквивалентную позицию, купив пут-опцион за 2,562 и базовый инструмент.
Проблема решится, если мы сначала рассчитаем ожидаемую стоимость базового инструмента по уравнению (5.10) с учетом того, что а i просто равно i (в нашем примере с DEGFDM = 5 ожидаемая стоимость базового инструмента равна 101,288467), и вычтем текущую цену базового инструмента из полученного значения: 101,288467 - 100= 1,288467. Теперь, если мы вычтем это значение из каждого значения а., т.е. внутренней стоимости из (5.11), и примем любые получившиеся значения менее 0 равными 0, тогда уравнение (5.11) даст нам теоретические значения, которые согласуются с (5.13). Таким образом, арифметическое математическое ожидание по базовому инструменту заменит текущую цену базового инструмента. В нашем примере (распределение Стьюдента с 5 степенями свободы) мы получим стоимость пут-опциона и колл-опциона с ценой исполнения 100, равную 3,218. Таким образом, наш ответ согласуется с уравнением (5.13), и возможность арбитража между этими двумя опционами и их базовыми инструментами отсутствует.
Когда мы используем распределение, которое основано на значениях арифметического математического ожидания базового инструмента на дату истечения и значение этого ожидания отличается от текущей стоимости базового инструмента, мы должны вычесть разность (ожидание - текущая стоимость) из внутренней стоимости опциона и приравнять нулю значения меньше нуля. Таким образом, для любой формы распределения уравнение (5.11) дает нам арифметическое математическое ожидание опциона на дату истечения, при условии, что арифметическое математическое ожидание по базовому инструменту равно его текущей цене (то есть направленное движение цены базового инструмента не предполагается).

 

[FXWizard]

Одиночная длинная позиция по опциону и оптимальное f

Рассмотрим обычную покупку колл-опциона. Вместо того чтобы для нахождения оптимального f использовать полную историю сделок по опционам данной рыночной системы, мы рассмотрим все возможные изменения цены данного опциона за время его существования и взвесим каждый результат вероятностью его осуществления. Этот взвешенный по вероятностям результат является HPR, соответствующим цене покупки опциона. Мы рассмотрим весь спектр результатов (т.е. среднее геометрическое) для каждого значения f и таким образом найдем оптимальное значение. Почти во всех моделях ценообразования опционов вводными переменными, имеющими наибольшее влияние на теоретическую цену опциона, являются: (а) время, оставшееся до истечения срока, (б) цена исполнения, (в) цена базового инструмента и (г) волатильность. Некоторые модели могут иметь и другие вводные данные, но именно эти четыре переменные больше всего влияют
на теоретическое значение. Из этих переменных две — время, оставшееся до истечения срока, и цена базового инструмента — переменные величины.
Волатильность тоже может изменяться, однако редко в той же степени, что цена базового инструмента или время до истечения срока. Цена исполнения не изменяется.
С помощью нашей модели можно найти теоретическую цену для всех значений цен базового инструмента и времени, оставшегося до истечения срока. Таким образом, HPR для опциона является функцией не только цены базового инструмента, но и функцией времени, оставшегося до даты истечения опциона:

где f = тестируемое значение f;
S = текущая цена опциона;
Z(T, U - Y) = теоретическая цена опциона, когда цена базового инструмента равна U - Y, а время, оставшееся до срока истечения, равно Т. Эту цену можно определить с помощью любой модели ценообразования, которую пользователь посчитает подходящей;
Р(Т, U) = 1-хвостая вероятность того, что цена базового инструмента равна U, когда время, оставшееся до истечения срока исполнения, равно Т. Это значение можно определить из любой формы распределения, которую пользователь посчитает подходящей;
Y = разность между арифметическим математическим ожиданием базового инструмента (согласно уравнению (5.10)) и текущей ценой.
С помощью этой формулы можно рассчитать HPR (взвешенное по вероятности результата) по сделке с опционом, при условии, что через время Т цена базового инструмента будет равна U. В данном уравнении переменная Т представляет собой долю года (выраженную десятичной дробью), оставшуюся до истечения срока опциона. Поэтому на дату истечения Т = 0. Если до истечения срока остается один год, то Т = 1. Переменная Z(T, U - Y) зависит от модели ценообразования, которую вы используете. Единственная переменная, которую вам надо рассчитать, — это Р(Т, U), т.е. вероятность того, что базовый инструмент будет равен U при заданном Т (т.е. времени, оставшемся до конца действия опциона). Если использовать модель Блэка-Шоулса или модель товарных опционов Блэка, то можно рассчитать Р(Т, U) следующим образом:
если U < или = О:

если U > Q:

где U = рассматриваемая цена;
Q = текущая цена базового инструмента;
V= годовая волатильность базового инструмента;
Е=доля года, выраженная десятичной дробью, прошедшая с тех пор, когда опцион был приобретен;
N() = функция нормального распределения (уравнение (3.21));
ln() = функция натурального логарифма.
В итоге мы получим взвешенное по вероятности HPR для каждого исхода.
Возможен широкий диапазон результатов, но, к сожалению, эти результаты не непрерывны. Например, время до истечения срока не задается непрерывной функцией. До истечения срока всегда остается целое число; то же верно и для цены базового инструмента. Если цена акции равна, например, 35, а минимальное изменение цены равно 1/8, то между 30 и 40 находится 81 возможное значение.
Зная время, через которое мы собираемся продать опцион, можно рассчитать взвешенные по вероятности HPR для всех возможных цен на этот рыночный день.
В нормальном распределении вероятности 99,73% всех результатов попадают в интервал трех стандартных отклонений от среднего, которое в нашем случае является текущей ценой базового инструмента. Поэтому нам необходимо рассчитать HPR для определенного рыночного дня и каждой дискретной цены между - 3 и + 3 стандартными отклонениями. Можно использовать 4, 5, 6 или больше стандартных отклонений, но ответ от этого не станет значительно точнее. Не следует также сокращать ценовое окно до 2 или 1 стандартного отклонения. Выбор 3
стандартньк отклонений, конечно, не является твердым правилом, но в большинстве случаев оно приемлемо. Если мы используем модель Блэка-Шоулса или модель опционов на фьючерсы Блэка, то можно узнать, какому изменению цены базового инструмента U соответствует 1 стандартное отклонение:

где U = текущая цена базового инструмента;
V = годовая волатильность базового инструмента;
Т = доля года, выраженная десятичной дробью, прошедшая с тех пор. когда опцион был приобретен;
ЕХР() = экспоненциальная функция.
Отметьте, что стандартное отклонение является функцией времени, прошедшего с момента открытия позиции.

 

[FXWizard]

Для точки, которая на Х стандартных отклонений выше текущей цены базового инструмента, получаем:

Для точки, которая на Х стандартных отклонений ниже текущей цены базового инструмента, получаем:

где U =текущая цена базового инструмента;
V =годовая волатильность базового инструмента;
Т =доля года, выраженная десятичной дробью, прошедшая с тех пор, когда опцион был приобретен;
EXPQ = экспоненциальная функция;
Х =число стандартных отклонений от среднего, для которых вы хо тите
определить вероятности.
Далее следует описание процедуры поиска оптимального f для данного опциона.
Шаг 1. Решите, закроете ли вы позицию по опциону в какой-то конкретный день.
Если нет, тогда в дальнейших расчетах используйте дату истечения срока
опциона.
Шаг 2. Определите, сколько дней вы будете удерживать позицию. Затем
преобразуйте это число дней в долю года, выраженную десятичной дробью.
Шаг 3. Для дня из шага 1 рассчитайте точки, которые находятся между +3 и -3 стандартными отклонениями.
Шаг 4. Преобразуйте диапазоны цен из шага 3 в дискретные значения. Другими словами, используя приращения по 1 тику, определите все возможные цены диапазона, включая крайние значения.
Шаг 5. Для каждого из полученных результатов рассчитайте Z(T, U - Y) и Р(Т, U), то есть рассчитайте теоретическую цену опциона, а также вероятность того, что базовый инструмент к рассматриваемым датам будет равен определенной цене.
Шаг 6. После того, как вы выполните шаг 5, у вас будут все входные данные, необходимые для расчета взвешенного по вероятности HPR.

где f = тестируемое значение f;
S = текущая цена опциона;
Z(T, U - Y) = теоретическая цена опциона, когда цена базового инструмента равна U - Y, а время, оставшееся до срока истечения, равно Т. Эту цену можно определить с помощью любой модели ценообразования, которую пользователь посчитает подходящей;
Р(Т, U) = 1-хвостая вероятность того, что цена базового инструмента равна U, когда время, оставшееся до истечения срока исполнения, равно Т. Это значение можно определить из любой формы распределения, которую пользователь посчитает подходящей;
Y = разность между арифметическим математическим ожиданием базового инструмента (согласно уравнению (5.10)) и текущей ценой.
Необходимо отметить, что форма распределения, используемого для Р(Т, U), не обязательно должна быть такой же, как и в модели ценообразования, применяемой для определения значений Z(T, U - Y). Например, вы используете модель фондовых опционов Блэка-Шоулса для определения значений Z(T, U - Y). Эта модель предполагает логарифмически нормальное распределение изменений цены,
однако для определения соответствующего Р(Т, U) вы можете использовать другую форму распределения.

 

[FXWizard]

Шаг 7. Теперь мы можем начать поиск оптимального f с помощью метода итераций, перебирая все возможные значения f между 0 и 1, или с помощью метода параболической интерполяции, или любого другого одномерного алгоритма поиска. Подставляя тестируемые значения f в HPR (у вас уже есть HPR для каждого из возможных приращений цены между + 3 и - 3 стандартными отклонениями на дату истечения срока или указанную дату выхода), вы можете найти среднее геометрическое для данного тестируемого значения f. Для этого надо перемножить все HPR, и полученное произведение возвести в степень единицы, деленной на сумма вероятностей:

поэтому

где G(f, T) = среднее геометрическое HPR для данного тестируемого значения f;
f = тестируемое значение f;
S = текущая цена опциона;
Z(T, U - Y) = теоретическая цена опциона, когда цена базового инструмента равна U - Y, а время, оставшееся до срока истечения, равно Т. Эту цену можно определить с помощью любой модели ценообразования,
которую пользователь посчитает подходящей;
Р(Т, U) = вероятность того, что базовый инструмент равен U, когда время, оставшееся до истечения срока исполнения, равно Т. Это значение можно определить из любой формы распределения, которую пользователь посчитает подходящей;
Y = разность между арифметическим математическим ожиданием базового инструмента (согласно уравнению (5.10)) и текущей ценой.
Значение f, которое в результате даст наибольшее среднее геометрическое, является оптимальным.
Мы можем оптимизировать f, определив оптимальную дату выхода. Другими словами, мы можем найти значение оптимального f для данного опциона на каждый день между текущим днем и днем истечения. Запишем оптимальные f и средние геометрические для каждой указанной даты выхода. Когда мы завершим эту процедуру, мы сможем найти ту дату выхода, которая даст наивысшее среднее геометрическое. Таким образом, мы получим день, когда должны выйти из позиции по опциону для того, чтобы математическое ожидание было наивысшим (т.е. среднее геометрическое было наивысшим). Мы также узнаем, какое оптимальное количество контрактов следует купить.
Теперь у нас есть математический метод, с помощью которого можно выходить из позиции по опциону и покупать опцион при положительном математическом ожидании. Если мы выйдем из позиции в день, когда среднее геометрическое максимально и оно больше 1,0, то следует покупать число контрактов, исходя из оптимального f, которое соответствует наивысшему среднему геометрическому.
Математическое ожидание, о котором мы говорим, — это геометрическое ожидание. Другими словами, среднее геометрическое (минус 1,0) является математическим ожиданием, когда вы реинвестируете прибыли (арифметическое положительное математическое ожидание будет, конечно же, выше, чем геометрическое).
После того как вы найдете оптимальное f для данного опциона, можно преобразовать полученное значение в число контрактов, которое следует покупать:

(5.19) K=INT(E/(S/f)),

где К = оптимальное число опционных контрактов для покупки;
f= значение оптимального Г(от 0 до 1);
S = текущая цена опциона;
Е = общий баланс счета;
1NT() = функция целой части.
Для расчета TWR следует знать, сколько раз мы хотели бы воспроизвести эту же сделку в будущем. Другими словами, если наше среднее геометрическое составляет 1,001 и необходимо найти TWR, которое соответствует этой же игре 100 раз подряд, то TWR будет 1,001^100 = 1,105115698. Поэтому можно ожидать заработка в 10,5115698%, если провести эту сделку 100 раз. Формула для преобразования среднего геометрического в TWR задается уравнением (4.18):

(4.18) TWR = Среднее геометрическое ^ X,

 

[FXWizard]

где TWR = относительный конечный капитал;
Х = число раз, которое мы «повторяем» эту игру.
Мы можем определить и другие побочные продукты, например, геометрическое математическое ожидание (среднее геометрическое минус 1). Если мы возьмем наибольший возможный проигрыш (стоимость самого опциона), разделим его на оптимальное f и умножим на геометрическое математическое ожидание, то получим среднюю геометрическую сделку. Как вы уже заметили, при использовании метода оптимального f в торговле опционами появляется еще один побочный продукт — оптимальная дата выхода. Мы рассматривали позиции по опционам при отсутствии направленного движения цены базового инструмента. Для указанной даты выхода точки, смещенные на 3 стандартных отклонения выше и ниже, рассчитываются из текущей цены, таким образом, мы ничего не знаем о будущем направлении цены базового инструмента. В соответствии с математическими моделями ценообразования мы не получим положительное арифметическое математическое ожидание, если будем удерживать позицию по опциону до срока истечения. Однако, как мы уже видели, можно достичь положительного геометрического математического ожидания, если закрыть позицию в определенный день до срока истечения.
Если вы предполагаете определенное изменение цены базового инструмента, его можно учесть. Допустим, мы рассматриваем опционы на базовый инструмент, который в настоящее время стоит 100. Далее предположим, что на основе анализа рынка выявлен тренд, который предполагает цену 105 к дате истечения, и эта дата отстоит на 40 рыночных дней от сегодняшней даты. Мы ожидаем, что цена
повысится на 5 пунктов за 40 дней. Если исходить из линейного изменения цены, то цена должна расти в среднем на 0,125 пунктов в день. Поэтому для завтрашнего дня (как дня выхода) мы возьмем значение U, равное 100,125. Для следующей даты выхода возьмем U, равное 100,25. К тому времени, когда указанная дата выхода станет датой истечения срока опциона, U будет равно 105. Если базовым инструментом является акция, то вы должны вычесть дивиденды из U, воспользовавшись уравнением (5.04). Тренд можно учитывать, если изменять каждый день значение U, исходя из сделанного прогноза. Так как уравнения (5.17а) и (5.176) изменятся, значения U повлияют на оптимальные f и побочные продукты. Отметьте, что в уравнениях (5.17а) и (5.176) используются новые значения U, т.е. происходит автоматическое приведение данных, следовательно, полученные оптимальные f будут основаны на данных, приведенных к текущей цене.
Когда вы будете использовать вышеописанную технику работы с оптимальным f, то заметите, что его значение каждый день меняется. Предположим, сегодня вы купили опцион и рассчитали оптимальную дату выхода. Послезавтра цена опциона может измениться, и если вы опять проведете процедуру расчета оптимального f, то также можете получить положительное математическое ожидание, но уже другую дату выхода. Что это означает?
Ситуация аналогична лошадиным бегам, где можно делать ставки после начала скачки и до их завершения. Шансы постоянно меняются, и вы в любой момент можете обменять купленный билет на деньги. Скажем, до начала скачек вы ставите 2 доллара на определенную лошадь, основываясь на положительном математическом ожидании, и лошадь после первого крута прибегает предпоследней. Предположим, ваш билет, купленный за 2 доллара, стоит теперь только 1,50 доллара.
Вы по-прежнему считаете, что математическое ожидание в пользу вашей лошади, исходя из результатов прошлых скачек и нынешних шансов. Вы решаете, что текущая цена билета в 1,50 доллара на 10% занижена. Можно получить деньги по билету, купленному до начала скачек за 2 доллара (сейчас он стоит 1,50 доллара), и можно также купить билет за 1,50 доллара, чтобы сделать еще одну ставку.
Таким образом, вы получаете положительное математическое ожидание, но на основе билета за 1,50 доллара, а не за 2 доллара. Та же аналогия применима и к опционам, позиция по которым в настоящий момент немного убыточна, но имеет положительное математическое ожидание на основе новой цены. Вы должны использовать другое оптимальное f для новой цены, регулируя текущую позицию (если это необходимо), и закрывать ее, исходя из новой оптимальной даты выхода.
Таким образом, вы используете последнюю ценовую информацию о базовом инструменте, что иногда может заставить вас удерживать позицию до истечения срока опциона. Возможность получения положительного математического ожидания при работе с опционами, которые теоретически справедливо оценены, сначала может показаться парадоксом или просто шарлатанством. Мы знаем, что теоретические цены опционов, найденные с помощью моделей, не позволяют получить положительное математическое ожидание (арифметическое) ни
покупателю, ни продавцу. Модели теоретически справедливы с поправкой «если удерживаются до истечения срока». Именно эта отсутствующая поправка позволяет опциону быть справедливо оцененным согласно моделям и все-таки иметь положительное ожидание. Помните, что цена опциона уменьшается со скоростью квадратного корня времени, оставшегося до истечения срока. Таким образом, после первого дня покупки опциона его премия должна упасть в меньшей степени, чем в последующие дни. Рассмотрим уравнения (5.17а) и (5.176) для цен,
соответствующих смещению на 4- Х и - Х стандартных величин по истечении времени Т. Окно цен каждый день расширяется, но все медленнее и медленнее, в первый день скорость расширения максимальна. Таким образом, в первый день падение премии по опциону будет минимальным, а окно Х стандартных отклонений будет расширяться быстрее всего. Чем меньше времени пройдет, тем с большей вероятностью мы будем иметь положительное ожидание по длинной позиции опциона, и чем шире окно Х стандартных отклонений, тем вероятнее, что мы будем иметь положительное ожидание, так как убыток ограничен ценой опциона, а возможная прибыль не ограничена. Между окном Х стандартных отклонений, которое с каждым днем становится все шире и шире (хотя со все более медленной скоростью), и премией опциона (падение которой с каждым днем происходит все быстрее и быстрее) происходит «перетягивание каната».
В первый день математическое ожидание максимально, хотя оно может и не быть положительным. Другими словами, математическое ожидание (арифметическое и геометрическое) самое большое после того, как вы продержали опцион 1 день (оно в действительности самое большое в тот момент, когда вы приобретаете опцион, и далее постепенно понижается, но мы рассматриваем дискретные величины).
Каждый последующий день ожидание понижается, но все медленнее и медленнее.
Следующая таблица иллюстрирует понижение ожидания по длинной позиции опциона. Этот пример уже упоминался в данной главе. Колл-опцион имеет ценуисполнения 100, базовый инструмент стоит также 100; дата истечения — 911220.
Волатильность составляет 20%, а сегодняшняя дата 911104. Мы используем формулу товарных опционов Блэка (Н определяется из уравнения (5.07), R = 5%) и 260,8875-дневный год. Возьмем 8 стандартных отклонений для расчета оптимального f, а минимальный шаг тика примем равным 0,1.

 

[FXWizard]

Значения столбца «AHPR» являются средними арифметическими HPR (расчет будет рассмотрен позднее в этой главе), a GHPR является средним геометрическим HPR. Столбец «f» представляет оптимальные f, из которых находятся значения столбцов AHPR и GHPR. Арифметическое математическое ожидание равно AHPR - 1, а геометрическое математическое ожидание равно GHPR - 1. Отметьте, что наибольшие математические ожидания (необязательно положительные ожидания, как в этом примере) возникают в день после приобретения опциона. Каждый последующий день ожидания уменьшаются, причем скорость уменьшения с течением времени замедляется. После 911106 математические ожидания (HPR - 1) становятся отрицательными. ' Если бы нам пришлось торговать по этой информации, мы могли бы войти сегодня (911104) и выйти при закрытии завтра (911105). Справедливая цена опциона равна 2,861. Если мы допустим, что он котируется по цене 100 долларов за полный пункт, цена опциона составит 2,861 * $100 ^ $286,10. Разделив эту цену на оптимальное f= 0,0806, мы найдем, что следует торговать одним опционом на каждые 3549,63 доллара на балансе счета.
Если бы мы держали опцион до закрытия 911106 (последний день), когда он все еще имеет положительное математическое ожидание, то открыв позицию сегодня, используя для дня выхода (911106) соответствующее оптимальное f= 0,0016, торговали бы 1 контрактом на каждые 178 812,50 доллара на балансе счета ($286,10 / 0,0016). Отметьте, что при этом ожидание намного ниже, чем в случае торговли 1 контрактом на каждые 3549,63 доллара на балансе счета и выхода по цене закрытия завтра (911105).
Скорость изменения между двумя функциями: уменьшением премии с течением времени и расширением окна Х стандартных отклонений, может создать положительное математическое ожидание для длинной позиции по опциону. Это ожидание имеет наибольшее значение в момент открытия позиции и после этого понижается с уменьшающейся скоростью. Таким образом, справедливо оцененный опцион (на основе вышеизложенных моделей) может иметь положительное математическое ожидание, если позицию по нему закрыть в начале периода падения премии. В следующей таблице рассматривается тот же колл-опцион с ценой исполнения 100, но на этот раз используются окна различного размера (различные значения стандартных отклонений):

AHPR и GHPR — это арифметические и геометрические HPR при оптимальном f для дня закрытия 911105 (самая благоприятная дата выхода, так как она имеет наивысшие AHPR и GHPR). f соответствует оптимальному f для 911105. Значения строки «Дата выхода» — это последние даты, когда еще существует положительное ожидание (т.е. когда AHPR и GHPR больше 1). Интересно отметить, что AHPR, GHPR, f и Дата выхода сходятся к определенным значениям, когда мы увеличиваем число стандартных отклонений. За пределами 5 стандартных отклонений эти значения едва заметно изменяются, за пределами 8 стандартных отклонений они практически вообще не изменяются. Недостатком использования большого числа стандартных отклонений является необходимость в значительном компьютерном времени. В нашем примере это не так важно, но когда мы будем рассматривать одновременную торговлю по нескольким позициям, вы увидите, что каждая дополнительная позиция экспоненциально увеличивает необходимое компьютерное время. Для одной позиции 8 стандартных отклонений более чем достаточно, однако для нескольких позиций, открытых одновременно, необходимо уменьшить число стандартных отклонений. Следует отметить, что правило 8 стандартных отклонений применимо только тогда, когда логарифмы изменений цены распределены нормально.

 

[FXWizard]

Одиночная короткая позиция по опциону

Все сказанное по поводу одиночной длинной опционной позиции остается верным и для одиночной короткой опционной позиции. Единственное отличие заключается в ином написании уравнения (5.14):

где HPR(T, U) = НРR для данного тестируемого значения Т и U;
f = тестируемое значение f;
S = текущая цена опциона;
Z(T, U - Y) = теоретическая цена опциона, когда цена базового инструмента равна U - Y, а время, оставшееся до срока истечения, равно Т, Р(Т, U) = вероятность того, что базовый инструмент равен U, когда время, оставшееся до истечения срока исполнения, равно Т;
Y = разность между арифметическим математическим ожиданием базового инструмента (согласно уравнению (5.10)) и текущей ценой.
Для одиночной короткой опционной позиции это уравнение преобразуется в:

где HPR(T, U) == HPR для данного тестируемого значения Т и U;
f= тестируемое значение f;
S = текущая цена опциона;
Z(T, U - Y)= теоретическая цена опциона, когда цена базового инструмента равна U - Y, а время, оставшееся до срока истечения, равно Т;
Р(Т, U) = вероятность того, что базовый инструмент равен U, когда время, оставшееся до истечения срока исполнения, равно Т, Y = разность между арифметическим математическим ожиданием базового инструмента (согласно уравнению (5.10)) и текущей ценой.
Обратите внимание, что единственным отличием уравнения (5.14) для одиночной длинной опционной позиции от уравнения (5.20) для одиночной короткой позиции является выражение (Z(T, U-Y)/S-1), которое заменяется на (1-Z(T, U - Y) / S). Все остальное в отношении одиночной длинной опционной позиции верно и для одиночной опционной короткой позиции.