- Форум
- Самоучитель трейдера
- Обучение трейдингу. Учебник и обсуждения
- Литература: Форекс, биржи, инвестиции
Вы используете устаревший браузер. Этот и другие сайты могут отображаться в нем неправильно.
Необходимо обновить браузер или попробовать использовать другой.
Необходимо обновить браузер или попробовать использовать другой.
Ральф Винс. Математика управления капиталом
- Автор темы FXWizard
- Дата начала
FXWizard
Гуру форума
Современная теория портфеля
Вспомните ситуацию с оптимальным f и проигрышем рыночной системы. Чем лучше рыночная система, тем выше значение f. Однако если вы торгуете с оптимальным f, проигрыш (исторически) никогда не может быть меньше f. Вообще говоря, чем лучше рыночная система, тем больше будут промежуточные проигрыши (в процентах от баланса счета), если торговать при оптимальном f. Таким образом, если вы хотите достичь наибольшего геометрического роста, то должны быть готовы к серьезным проигрышам на своем пути.
Эффективная диверсификация, путем включения в портфель других рыночных систем, является лучшим способом, которым можно смягчить этот проигрыш и преодолеть его, все еще оставаясь близко к пику кривой f (то есть не уменьшая f, скажем, до f/2). Когда одна рыночная система приносит убыток, другая приносит прибыль, тем самым смягчая проигрыш первой. Это также оказывает большое влияние на весь счет. Рыночная система, которая только что испытала проигрыш (и теперь возвращается к хорошей работе), будет иметь не меньше средств, чем до убытка (благодаря тому, что другая рыночная система аннулировала проигрыш). Диверсификация не будет сдерживать прирост системы (наоборот, движение вверх будет быстрее, так как после проигрыша вы не начнете с меньшего числа контрактов), при этом она смягчает понижение баланса (но только до очень ограниченной степени). Можно рассчитать оптимальный портфель, состоящий из различных рыночных систем с соответствующими оптимальными f. Хотя мы не можем быть полностью уверены, что оптимальный в прошлом портфель будет оптимальным и в будущем, это все же более вероятно, чем то, что прошлые оптимальные параметры системы будут оптимальными или приблизительно оптимальными в будущем. В то время как оптимальные параметры системы с течением времени меняются довольно быстро, веса отдельных систем в оптимальном портфеле меняются очень медленно (как и значения оптимальных f).
Вообще, корреляция между рыночными системами достаточно стабильна. Эта новость будет еще более приятна для трейдера, если он уже нашел такой оптимально смешанный портфель.
Вспомните ситуацию с оптимальным f и проигрышем рыночной системы. Чем лучше рыночная система, тем выше значение f. Однако если вы торгуете с оптимальным f, проигрыш (исторически) никогда не может быть меньше f. Вообще говоря, чем лучше рыночная система, тем больше будут промежуточные проигрыши (в процентах от баланса счета), если торговать при оптимальном f. Таким образом, если вы хотите достичь наибольшего геометрического роста, то должны быть готовы к серьезным проигрышам на своем пути.
Эффективная диверсификация, путем включения в портфель других рыночных систем, является лучшим способом, которым можно смягчить этот проигрыш и преодолеть его, все еще оставаясь близко к пику кривой f (то есть не уменьшая f, скажем, до f/2). Когда одна рыночная система приносит убыток, другая приносит прибыль, тем самым смягчая проигрыш первой. Это также оказывает большое влияние на весь счет. Рыночная система, которая только что испытала проигрыш (и теперь возвращается к хорошей работе), будет иметь не меньше средств, чем до убытка (благодаря тому, что другая рыночная система аннулировала проигрыш). Диверсификация не будет сдерживать прирост системы (наоборот, движение вверх будет быстрее, так как после проигрыша вы не начнете с меньшего числа контрактов), при этом она смягчает понижение баланса (но только до очень ограниченной степени). Можно рассчитать оптимальный портфель, состоящий из различных рыночных систем с соответствующими оптимальными f. Хотя мы не можем быть полностью уверены, что оптимальный в прошлом портфель будет оптимальным и в будущем, это все же более вероятно, чем то, что прошлые оптимальные параметры системы будут оптимальными или приблизительно оптимальными в будущем. В то время как оптимальные параметры системы с течением времени меняются довольно быстро, веса отдельных систем в оптимальном портфеле меняются очень медленно (как и значения оптимальных f).
Вообще, корреляция между рыночными системами достаточно стабильна. Эта новость будет еще более приятна для трейдера, если он уже нашел такой оптимально смешанный портфель.
Систематик
Активный участник
"Лучшая ситстема" - та. что дает наибольшую прибыль, так ведь. Но почему тогда по ней больше промежуточные проигрыши? И кстати по портфелям систем: для себя не вижу реальности использовать много систем одновременно. Только те, кторорые имеют разный тф, у меня есть одна, которая дает сделки несколько раз в месяц всего, а так на часовиках не каждый день правда. И есть еще на мелком интервале. Но она требует большего времени, не всегда есть. Или имеется в виду диверсификация на одном ТФ?
FXWizard
Гуру форума
Модель Марковица
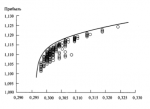
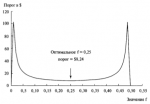
Основные концепции современной теории портфеля изложены в монографии, написанной доктором Гарри Марковицем. Первоначально Марковиц предположил, что управление портфелем является проблемой структурного, а не индивидуального выбора акций, что обычно практикуется. Марковиц доказывал, что диверсификация эффективна только тогда, когда корреляция между включенными в портфель рынками имеет отрицательное значение. Если у нас есть портфель, составленный из одного вида акций, то наилучшая диверсификация достигается в том случае, если мы выберем другой вид акций, которые имеют минимально возможную корреляцию с ценой первой акции. В результате этого. портфель в целом (если он состоит из этих двух видов акций с отрицательной корреляцией) будет иметь меньшую дисперсию, чем любой вид акций, взятый отдельно. Марковиц предположил, что инвесторы действуют рациональным способои и при наличии выбора предпочитают портфель с меньшим риском при равном уровне прибыльности или выбирают портфель с большей прибылью, при одинаковом риске. Далее Марковиц утверждает, что для данного уровня риска есть оптимальный портфель с наивысшей доходностью, и таким же образом для данного уровня доходности есть оптимальный портфель с наименьшим риском. Портфель, доходность которого может быть увеличена без сопутствующего увеличения риска или портфель, риск которого можно уменьшить без сопутствующего уменьшения доходности, согласно Марковицу, неэффективны. Рисунок 1-7 показывает все имеющиеся портфели, рассматриваемые в данном примере. Если у вас портфель С, то лучше заменить его на портфель А, где при- быль такая же, но с меньшим риском, или на портфель В, где вы получите боль- шую прибыль при том же риске. Описывая эту ситуацию, Марковиц ввел понятие «эффективная граница» (efficient frontier). Это набор портфелей, которые находятся в верхней левой части графика, то есть портфели, прибыль которых больше не может быть увеличена без увеличения риска, и риск которых не может быть уменьшен без уменьшения прибыли. Портфели, находящиеся на эффективной границе, называются эффективными портфелями (см. Рисунок 1-8). Портфели, которые находятся вверху справа и внизу слева, в целом недостаточно диверсифицированы по сравнению с другими портфелями. Те же портфели, которые находятся в середине эффективной границы, обычно очень хорошо диверсифицированы. Выбор портфеля инвестором зависит от степени неприятия риска инвестором — иначе говоря, от желания взять на себя риск. В модели Марковица любой портфель, который находится на эффективной границе, является хорошим выбором, но какой именно портфель выберет инвестор — это вопрос личного предпочтения (позднее мы увидим, что есть точное оптимальное расположение портфеля на эффективной границе для всех инвесторов).
Модель Марковица первоначально была представлена для портфеля акций, который инвестор будет держать достаточно долго. Поэтому основными входными данными были ожидаемые доходы по акциям (определяется как ожидаемый прирост цены акции плюс дивиденды), ожидаемые дисперсии этих доходов и корреляции доходов между различными акциями. Если бы мы

Рисунок 1-7 Современная теория портфеля

Рисунок 1-8 Эффективная граница
перенесли эту концепцию на фьючерсы, то было бы разумным (так как по фьючерсам не выплачивают дивидендов) измерять ожидаемое повышение цены, дисперсию и корреляции различных фьючерсов. Возникает вопрос: «Если мы измеряем корреляцию цен, то что произойдет при включении в портфель двух систем с отрицательной корреляцией, работающих на одном и том же рынке?» Допустим, у нас есть системы А и В с отрицательной корреляцией. Когда А в проигрыше, В в выигрыше, и наоборот. Разве это не идеальная диверсификация? Действительно, мы хотим измерить не корреляции цен рынков, на которых работаем, а корреляции изменений ежедневных балансов различных рыночных систем. И все-таки это является сравнением яблок и апельсинов. Скажем, две рыночные системы, корреляции которых мы собираемся измерить, работают на одном и том же рынке, и одна из систем имеет оптимальное f, соответствующее 1 контракту на каждые 2000 долларов на счете, а другая система имеет оптимальное f, соответствующее 1 контракту на каждые 10 000 долларов на счете. Чтобы понять суть торговли фиксированной долей в портфеле из нескольких систем, мы переведем изменения ежедневного баланса для данной рыночной системы в ежедневные HPR. HPR в этом контексте означает, сколько заработано или проиграно в данный день на основе 1 контракта в зависимости от оптимального f для этой системы. Рассмотрим пример. Скажем, рыночная система с оптимальным f в 2000 долларов за день заработала 100 долларов. Тогда HPR для этой рыночной системы составит 1,05. Дневное HPR можно найти следующим образом:

где А = сумма в долларах, выигранная или проигранная за этот день; В = оптимальное f в долларах.
Для рассматриваемых рыночных систем преобразуем дневные выигрыши и про- игрыши в дневные HPR, тогда мы получим значение, не зависящее от количества контрактов. В указанном примере, где дневное HPR составляет 1,05, вы выиграли 5%. Эти 5% не зависят от того, был у вас 1 контракт или 1000 контрактов. Теперь можно сравнивать разные портфели. Мы будем сравнивать все возможные ком- бинации портфелей, начиная с портфелей, состоящих из одной рыночной системы (для каждой рассматриваемой рыночной системы), заканчивая портфелями из N рыночных систем. В качестве примера рассмотрим рыночные системы А, В и С, их комбинации будут выглядеть следующим образом:
А
В
С
АВ
АС
ВС
АВС
Но не будем останавливаться на этом. Для каждой комбинации рассчитаем веса рыночных систем в портфеле. Для этого необходимо задать минимальный про- центный вес системы (или минимальное изменение веса). В следующем примере (портфель из систем А, В, С) этот минимальный вес системы равен 10% (0,10):
А 100%
В 100%
С 100%
АВ 90% 10%
80% 20%
30% 70%
60% 40%
50% 50%
40% 60%
30% 70%
20% 80%
10% 90%
АС 90% 10%
80% 20%
70% 30%
60% 40%
50% 50%
40% 60%
30% 70%
20% 80%
10% 90%
ВС 90% 10%
80% 20%
70% 30%
60% 40%
50% 50%
40% 60%
30% 70%
20% 80%
10% 90%
АВС 80% 10% 10%
70% 20% 10%
70% 10% 20%
10% 30% 60%
10% 20% 70%
10% 10% 80%
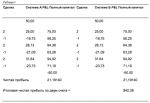
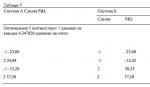
Введем понятие КСП (комбинация систем в портфеле). Теперь для каждой КСП рассчитаем совокупное HPR для отдельного дня. Совокупное HPR для данного дня будет суммой HPR каждой рыночной системы для этого дня, умноженных на процентные веса систем. Например, для систем А, В и С мы рассматриваем про- центные веса 10%, 50%, 40% соответственно. Далее допустим, что отдельные HPR для этих рыночных систем в тот день были 0,9, 1,4 и 1,05 соответственно. Тогда совокупное HPR для этого дня будет:
Совокупное HPR = (0,9 * 0,1) + (1,4 * 0,5) + (1,05 * 0,4) = 0,09 + 0,7 + 0,42 =1,21
Теперь нанесем дневные HPR для каждой КСП на ось Y В модели Марковица это соответствует получаемому доходу. На оси Х отложим стандартное отклонение дневных HPR для каждой КСП. В модели Марковица это соответствует риску. Современную теорию портфеля часто называют Теорией Е -V, что соответствует названиям осей. Вертикальную ось часто называют Е — ожидаемая прибыль (expected return), а горизонтальную ось называют V — дисперсия ожидаемой при- были (variance in expected returns). После этого можно найти эффективную границу. Мы включили различные рынки, системы и факторы f и теперь можем
количественно определить лучшие КСП (то есть КСП, которые находятся вдоль эффективной границы).
Основные концепции современной теории портфеля изложены в монографии, написанной доктором Гарри Марковицем. Первоначально Марковиц предположил, что управление портфелем является проблемой структурного, а не индивидуального выбора акций, что обычно практикуется. Марковиц доказывал, что диверсификация эффективна только тогда, когда корреляция между включенными в портфель рынками имеет отрицательное значение. Если у нас есть портфель, составленный из одного вида акций, то наилучшая диверсификация достигается в том случае, если мы выберем другой вид акций, которые имеют минимально возможную корреляцию с ценой первой акции. В результате этого. портфель в целом (если он состоит из этих двух видов акций с отрицательной корреляцией) будет иметь меньшую дисперсию, чем любой вид акций, взятый отдельно. Марковиц предположил, что инвесторы действуют рациональным способои и при наличии выбора предпочитают портфель с меньшим риском при равном уровне прибыльности или выбирают портфель с большей прибылью, при одинаковом риске. Далее Марковиц утверждает, что для данного уровня риска есть оптимальный портфель с наивысшей доходностью, и таким же образом для данного уровня доходности есть оптимальный портфель с наименьшим риском. Портфель, доходность которого может быть увеличена без сопутствующего увеличения риска или портфель, риск которого можно уменьшить без сопутствующего уменьшения доходности, согласно Марковицу, неэффективны. Рисунок 1-7 показывает все имеющиеся портфели, рассматриваемые в данном примере. Если у вас портфель С, то лучше заменить его на портфель А, где при- быль такая же, но с меньшим риском, или на портфель В, где вы получите боль- шую прибыль при том же риске. Описывая эту ситуацию, Марковиц ввел понятие «эффективная граница» (efficient frontier). Это набор портфелей, которые находятся в верхней левой части графика, то есть портфели, прибыль которых больше не может быть увеличена без увеличения риска, и риск которых не может быть уменьшен без уменьшения прибыли. Портфели, находящиеся на эффективной границе, называются эффективными портфелями (см. Рисунок 1-8). Портфели, которые находятся вверху справа и внизу слева, в целом недостаточно диверсифицированы по сравнению с другими портфелями. Те же портфели, которые находятся в середине эффективной границы, обычно очень хорошо диверсифицированы. Выбор портфеля инвестором зависит от степени неприятия риска инвестором — иначе говоря, от желания взять на себя риск. В модели Марковица любой портфель, который находится на эффективной границе, является хорошим выбором, но какой именно портфель выберет инвестор — это вопрос личного предпочтения (позднее мы увидим, что есть точное оптимальное расположение портфеля на эффективной границе для всех инвесторов).
Модель Марковица первоначально была представлена для портфеля акций, который инвестор будет держать достаточно долго. Поэтому основными входными данными были ожидаемые доходы по акциям (определяется как ожидаемый прирост цены акции плюс дивиденды), ожидаемые дисперсии этих доходов и корреляции доходов между различными акциями. Если бы мы
Рисунок 1-7 Современная теория портфеля
Рисунок 1-8 Эффективная граница
перенесли эту концепцию на фьючерсы, то было бы разумным (так как по фьючерсам не выплачивают дивидендов) измерять ожидаемое повышение цены, дисперсию и корреляции различных фьючерсов. Возникает вопрос: «Если мы измеряем корреляцию цен, то что произойдет при включении в портфель двух систем с отрицательной корреляцией, работающих на одном и том же рынке?» Допустим, у нас есть системы А и В с отрицательной корреляцией. Когда А в проигрыше, В в выигрыше, и наоборот. Разве это не идеальная диверсификация? Действительно, мы хотим измерить не корреляции цен рынков, на которых работаем, а корреляции изменений ежедневных балансов различных рыночных систем. И все-таки это является сравнением яблок и апельсинов. Скажем, две рыночные системы, корреляции которых мы собираемся измерить, работают на одном и том же рынке, и одна из систем имеет оптимальное f, соответствующее 1 контракту на каждые 2000 долларов на счете, а другая система имеет оптимальное f, соответствующее 1 контракту на каждые 10 000 долларов на счете. Чтобы понять суть торговли фиксированной долей в портфеле из нескольких систем, мы переведем изменения ежедневного баланса для данной рыночной системы в ежедневные HPR. HPR в этом контексте означает, сколько заработано или проиграно в данный день на основе 1 контракта в зависимости от оптимального f для этой системы. Рассмотрим пример. Скажем, рыночная система с оптимальным f в 2000 долларов за день заработала 100 долларов. Тогда HPR для этой рыночной системы составит 1,05. Дневное HPR можно найти следующим образом:
где А = сумма в долларах, выигранная или проигранная за этот день; В = оптимальное f в долларах.
Для рассматриваемых рыночных систем преобразуем дневные выигрыши и про- игрыши в дневные HPR, тогда мы получим значение, не зависящее от количества контрактов. В указанном примере, где дневное HPR составляет 1,05, вы выиграли 5%. Эти 5% не зависят от того, был у вас 1 контракт или 1000 контрактов. Теперь можно сравнивать разные портфели. Мы будем сравнивать все возможные ком- бинации портфелей, начиная с портфелей, состоящих из одной рыночной системы (для каждой рассматриваемой рыночной системы), заканчивая портфелями из N рыночных систем. В качестве примера рассмотрим рыночные системы А, В и С, их комбинации будут выглядеть следующим образом:
А
В
С
АВ
АС
ВС
АВС
Но не будем останавливаться на этом. Для каждой комбинации рассчитаем веса рыночных систем в портфеле. Для этого необходимо задать минимальный про- центный вес системы (или минимальное изменение веса). В следующем примере (портфель из систем А, В, С) этот минимальный вес системы равен 10% (0,10):
А 100%
В 100%
С 100%
АВ 90% 10%
80% 20%
30% 70%
60% 40%
50% 50%
40% 60%
30% 70%
20% 80%
10% 90%
АС 90% 10%
80% 20%
70% 30%
60% 40%
50% 50%
40% 60%
30% 70%
20% 80%
10% 90%
ВС 90% 10%
80% 20%
70% 30%
60% 40%
50% 50%
40% 60%
30% 70%
20% 80%
10% 90%
АВС 80% 10% 10%
70% 20% 10%
70% 10% 20%
10% 30% 60%
10% 20% 70%
10% 10% 80%
Введем понятие КСП (комбинация систем в портфеле). Теперь для каждой КСП рассчитаем совокупное HPR для отдельного дня. Совокупное HPR для данного дня будет суммой HPR каждой рыночной системы для этого дня, умноженных на процентные веса систем. Например, для систем А, В и С мы рассматриваем про- центные веса 10%, 50%, 40% соответственно. Далее допустим, что отдельные HPR для этих рыночных систем в тот день были 0,9, 1,4 и 1,05 соответственно. Тогда совокупное HPR для этого дня будет:
Совокупное HPR = (0,9 * 0,1) + (1,4 * 0,5) + (1,05 * 0,4) = 0,09 + 0,7 + 0,42 =1,21
Теперь нанесем дневные HPR для каждой КСП на ось Y В модели Марковица это соответствует получаемому доходу. На оси Х отложим стандартное отклонение дневных HPR для каждой КСП. В модели Марковица это соответствует риску. Современную теорию портфеля часто называют Теорией Е -V, что соответствует названиям осей. Вертикальную ось часто называют Е — ожидаемая прибыль (expected return), а горизонтальную ось называют V — дисперсия ожидаемой при- были (variance in expected returns). После этого можно найти эффективную границу. Мы включили различные рынки, системы и факторы f и теперь можем
количественно определить лучшие КСП (то есть КСП, которые находятся вдоль эффективной границы).
Вложения
FXWizard
Гуру форума
Стратегия среднего геометрического портфеля
В какой именно точке на эффективной границе вы будете находиться (то есть ка- кова эффективная КСП), является функцией вашего собственного неприятия риска, по крайней мере, в соответствии с моделью Марковица. Однако есть оптимальная точка на эффективной границе, и с помощью математических методов можно найти эту точку. Если вы выберете КСП с наивысшим средним геометрическим HPR, то достигнете оптимальной КСП! Мы можем рассчитать среднее геометрическое из среднего арифметического HPR и стандартного отклонения HPR (обе эти величины у нас уже есть, так как они являются осями Х и Y модели Марковица!) Уравнения (1.16а) и (1.166) дают нам формулу для оценочного сред- него геометрического EGM (estimated geometric mean). Данный расчет очень бли- зок (обычно до четвертого или пятого знака после запятой) к реальному среднему геометрическому, поэтому можно использовать оценочное среднее геометрическое вместо реального среднего геометрического.


где EGM == оценочное среднее геометрическое;
AHPR = среднее арифметическое HPR, или координата, соответствующая доходу по портфелю;
SD = стандартное отклонение HPR, или координата, соответствующая риску по портфелю;
V = дисперсия HPR, равная SD ^ 2. Обе формы уравнения (1.16) эквивалентны.
При КСП с наивысшим средним геометрическим рост стоимости портфеля бу- дет максимальным; более того, данная КСП позволит достичь определенного уровня баланса за минимальное время.
В какой именно точке на эффективной границе вы будете находиться (то есть ка- кова эффективная КСП), является функцией вашего собственного неприятия риска, по крайней мере, в соответствии с моделью Марковица. Однако есть оптимальная точка на эффективной границе, и с помощью математических методов можно найти эту точку. Если вы выберете КСП с наивысшим средним геометрическим HPR, то достигнете оптимальной КСП! Мы можем рассчитать среднее геометрическое из среднего арифметического HPR и стандартного отклонения HPR (обе эти величины у нас уже есть, так как они являются осями Х и Y модели Марковица!) Уравнения (1.16а) и (1.166) дают нам формулу для оценочного сред- него геометрического EGM (estimated geometric mean). Данный расчет очень бли- зок (обычно до четвертого или пятого знака после запятой) к реальному среднему геометрическому, поэтому можно использовать оценочное среднее геометрическое вместо реального среднего геометрического.
где EGM == оценочное среднее геометрическое;
AHPR = среднее арифметическое HPR, или координата, соответствующая доходу по портфелю;
SD = стандартное отклонение HPR, или координата, соответствующая риску по портфелю;
V = дисперсия HPR, равная SD ^ 2. Обе формы уравнения (1.16) эквивалентны.
При КСП с наивысшим средним геометрическим рост стоимости портфеля бу- дет максимальным; более того, данная КСП позволит достичь определенного уровня баланса за минимальное время.
Вложения
FXWizard
Гуру форума
Ежедневные процедуры при использовании оптимальных портфелей
Посмотрим на примере, как применять вышеописанный подход на ежедневной основе. Допустим, что оптимальное КСП соответствует трем различным рыночным системам. Предположим, что процент размещения составляет 10%, 50% и 40%. Если бы вы рассматривали счет в 50 000 долларов, то он был бы «разделен» на три субсчета в 5000, 25 000 и 20 000 долларов для каждой рыночной системы (А, В и С) соответственно. Затем для баланса по субсчету каждой рыночной системы вычислите, сколькими контрактами торговать. Скажем, фактор f дал следующие величины:
Рыночная система А: 1 контракт на $5000 баланса счета. Рыночная система В: 1 контракт на $2500 баланса счета. Рыночная система С: 1 контракт на $2000 баланса счета.

Тогда вы будете торговать 1 контрактом для рыночной системы А ($5000 / $5000), 10 контрактами для рыночной системы В ($25 000 / $2500) и 10 контрактами для рыночной системы С ($20 000 / $2000). Каждый день, когда общий баланс счета изменяется, все субсчета перерассчитываются. Допустим, что счет в 50 000 долларов на следующий день понизился до 45000 долларов. Так как мы каждый день заново перераспределяем средства по субсчетам, то получаем 4500 долларов для рыночной системы А, 22 500 долларов для рыночной системы В, и 18 000 долларов для рыночной системы субсчета С. На следующий день мы будем торговать нулевым количеством контрактов по рыночной системе А ($4500 / $5000 = 0,9, или, так как мы всегда основываемся на целых числах, 0), 9 контрактами для рыночной системы В ($22 500 / $2500), и 9 контрактами для рыночной системы С ($18 000 / $2000). Перерассчитывайте субсчета ежедневно, независимо от того, что вы получили: прибыль или убыток. Помните, субсчета, использованные здесь, являются условной конструкцией.
Есть более простой для понимания способ, дающий те же самые ответы, — деление оптимального f рыночной системы на ее процентный вес. Это даст сумму в долларах, на которую мы затем разделим общий баланс счета, чтобы узнать, сколькими контрактами торговать. Так как баланс счета изменяется ежедневно, мы перерассчитываем субсчета также ежедневно для получения нового общего баланса счета. В рассмотренном примере рыночная система А, при значении f в 1 контракт на 5000 долларов баланса счета и процентном весе 10%, соответствует 1 контракту на 50 000 долларов общего баланса счета ($5000 / 0,10). Рыночная система В, при значении IB 1 контракт на 2500 долларов баланса счета и процен- тном весе 50%, соответствует 1 контракту на 5000 долларов общего баланса счета ($2500 / 0,50). Рыночная система С, при значении IB 1 контракт на 2000 долларов баланса счета и процентном весе 40%, соответствует 1 контракту на 5000 долларов общего баланса счета ($2000 / 0,40). Таким образом, если бы у нас было 50 000 долларов на счете, мы бы торговали 1 контрактом в рыночной системе А, 10 контрактами в рыночной системе В и 10 контрактами в рыночной системе С. На следующий день процедура повторяется. Скажем, наш общий баланс счета повысился до 59 000 долларов. В этом случае разделим 59 000 долларов на 50 000 долларов и получим 1,18 (или округляя до целого числа 1), поэтому завтра мы бы торговали 1 контрактом в рыночной системе А, 11 контрактами ($59 000 / $5000 =11,8, что ближе к целому числу 11) в рыночной системе В и 11 контрактами в рыночной системе С. Предположим, в рыночной системе С со вчерашнего дня у нас открыта длинная позиция на 10 контрактов. Нам не следует добавлять сегодня до 11 контрактов. Суммы, которые мы рассчитываем с использованием баланса, рассчитываются только для новь1х позиций. Поэтому завтра (если было открыто 10 контрактов, но мы закрыли позицию, т.е. зафиксировали прибыль) нам следует открыть 11 контрактов, если мы посчитаем это целесообразным. Расчет оптимального портфеля с использованием ежедневных HPR означает, что нам следует входить на рынок и изменять позиции на ежедневной основе, а не от сделки к сделке; но это не обязательно делать, если вы будете торговать по долгосрочной системе, поскольку вам будет невыгодно регулировать размер позиции на ежедневной основе из-за высоких накладных расходов. Вообще говоря, вам следует изменять позиции на ежедневной основе, но в реальной жизни вы можете изменять их от сделки к сделке с малой потерей точности. Применение правильных дневных позиций не является большой проблемой. Вспомните, что при поиске оптимального портфеля мы использовали в качестве вводных данных дневные HPR. Поэтому нам следовало бы изменять размер позиции ежедневно (если бы мы могли изменять каждую позицию по цене, по которой она закрылась вчера). В действительности это становится непрактично, так как издержки на трансакции начинают перевешивать прибыли от ежедневного изменения позиций. С другой стороны, если мы открываем позицию, которую собираемся удерживать в течение года, нам следует пересматривать ее чаще, чем раз в год (т.е. в конце срока, когда мы откроем другую позицию). Вообще, в подобных долгосрочных системах нам лучше регулировать позицию каждую неделю, а не каждый день. Аргументация здесь такова: потери из-за не совсем правильных дневных позиций могут быть меньше, чем дополнительные издержки по сделкам для ежедневного изменения позиций. Вы должны определить, основываясь на используемой тор- говой стратегии, какие из потерь будут для вас меньше. Какой объем исторических данных необходим для расчета оптимальных портфелей? Этот вопрос можно сформулировать несколько иначе: «Какой объем исторических данных необходим для определения оптимального f данной рыночной системы?» Точного ответа не существует. Вообще, чем больше исторических данных вы используете, тем лучше должен быть результат (то есть оптимальные портфели в будущем будут напоминать нынешние оптимальные портфели, рассчитанные по историческим данным). Однако соотношения изменяются, хотя и медленно. Одна из проблем при использовании данных за слишком большой период времени заключается в том, что возникает тенденция к использованию в портфеле рынков, которые были активны в прошлом. Например, если бы вы создавали портфель в 1983 году на 5 годах прошлых данных, то, вероятнее всего, один из драгоценных металлов оказался бы частью оптимального портфеля. Однако торговые системы по драгоценным металлам работали в большинстве своем очень плохо на протяжении нескольких лет после 1980-1981 годов. Поэтому, как видите, при определении будущего оптимального портфеля между использованием слишком большого количества исторических данных и использованием слишком малого количества данных нужно найти золотую середину. И, наконец, возникает вопрос, как часто следует повторять всю процедуру поиска оптимального портфеля. По большому счету вы должны делать это постоянно. Однако в реальной жизни достаточно тестировать портфель каждые 3 месяца. И даже если производить эту операцию каждые 3 месяца, все еще есть высокая вероятность, что вы придете к тому же составу портфеля или очень сходному с тем, что создали ранее.
Посмотрим на примере, как применять вышеописанный подход на ежедневной основе. Допустим, что оптимальное КСП соответствует трем различным рыночным системам. Предположим, что процент размещения составляет 10%, 50% и 40%. Если бы вы рассматривали счет в 50 000 долларов, то он был бы «разделен» на три субсчета в 5000, 25 000 и 20 000 долларов для каждой рыночной системы (А, В и С) соответственно. Затем для баланса по субсчету каждой рыночной системы вычислите, сколькими контрактами торговать. Скажем, фактор f дал следующие величины:
Рыночная система А: 1 контракт на $5000 баланса счета. Рыночная система В: 1 контракт на $2500 баланса счета. Рыночная система С: 1 контракт на $2000 баланса счета.

Тогда вы будете торговать 1 контрактом для рыночной системы А ($5000 / $5000), 10 контрактами для рыночной системы В ($25 000 / $2500) и 10 контрактами для рыночной системы С ($20 000 / $2000). Каждый день, когда общий баланс счета изменяется, все субсчета перерассчитываются. Допустим, что счет в 50 000 долларов на следующий день понизился до 45000 долларов. Так как мы каждый день заново перераспределяем средства по субсчетам, то получаем 4500 долларов для рыночной системы А, 22 500 долларов для рыночной системы В, и 18 000 долларов для рыночной системы субсчета С. На следующий день мы будем торговать нулевым количеством контрактов по рыночной системе А ($4500 / $5000 = 0,9, или, так как мы всегда основываемся на целых числах, 0), 9 контрактами для рыночной системы В ($22 500 / $2500), и 9 контрактами для рыночной системы С ($18 000 / $2000). Перерассчитывайте субсчета ежедневно, независимо от того, что вы получили: прибыль или убыток. Помните, субсчета, использованные здесь, являются условной конструкцией.
Есть более простой для понимания способ, дающий те же самые ответы, — деление оптимального f рыночной системы на ее процентный вес. Это даст сумму в долларах, на которую мы затем разделим общий баланс счета, чтобы узнать, сколькими контрактами торговать. Так как баланс счета изменяется ежедневно, мы перерассчитываем субсчета также ежедневно для получения нового общего баланса счета. В рассмотренном примере рыночная система А, при значении f в 1 контракт на 5000 долларов баланса счета и процентном весе 10%, соответствует 1 контракту на 50 000 долларов общего баланса счета ($5000 / 0,10). Рыночная система В, при значении IB 1 контракт на 2500 долларов баланса счета и процен- тном весе 50%, соответствует 1 контракту на 5000 долларов общего баланса счета ($2500 / 0,50). Рыночная система С, при значении IB 1 контракт на 2000 долларов баланса счета и процентном весе 40%, соответствует 1 контракту на 5000 долларов общего баланса счета ($2000 / 0,40). Таким образом, если бы у нас было 50 000 долларов на счете, мы бы торговали 1 контрактом в рыночной системе А, 10 контрактами в рыночной системе В и 10 контрактами в рыночной системе С. На следующий день процедура повторяется. Скажем, наш общий баланс счета повысился до 59 000 долларов. В этом случае разделим 59 000 долларов на 50 000 долларов и получим 1,18 (или округляя до целого числа 1), поэтому завтра мы бы торговали 1 контрактом в рыночной системе А, 11 контрактами ($59 000 / $5000 =11,8, что ближе к целому числу 11) в рыночной системе В и 11 контрактами в рыночной системе С. Предположим, в рыночной системе С со вчерашнего дня у нас открыта длинная позиция на 10 контрактов. Нам не следует добавлять сегодня до 11 контрактов. Суммы, которые мы рассчитываем с использованием баланса, рассчитываются только для новь1х позиций. Поэтому завтра (если было открыто 10 контрактов, но мы закрыли позицию, т.е. зафиксировали прибыль) нам следует открыть 11 контрактов, если мы посчитаем это целесообразным. Расчет оптимального портфеля с использованием ежедневных HPR означает, что нам следует входить на рынок и изменять позиции на ежедневной основе, а не от сделки к сделке; но это не обязательно делать, если вы будете торговать по долгосрочной системе, поскольку вам будет невыгодно регулировать размер позиции на ежедневной основе из-за высоких накладных расходов. Вообще говоря, вам следует изменять позиции на ежедневной основе, но в реальной жизни вы можете изменять их от сделки к сделке с малой потерей точности. Применение правильных дневных позиций не является большой проблемой. Вспомните, что при поиске оптимального портфеля мы использовали в качестве вводных данных дневные HPR. Поэтому нам следовало бы изменять размер позиции ежедневно (если бы мы могли изменять каждую позицию по цене, по которой она закрылась вчера). В действительности это становится непрактично, так как издержки на трансакции начинают перевешивать прибыли от ежедневного изменения позиций. С другой стороны, если мы открываем позицию, которую собираемся удерживать в течение года, нам следует пересматривать ее чаще, чем раз в год (т.е. в конце срока, когда мы откроем другую позицию). Вообще, в подобных долгосрочных системах нам лучше регулировать позицию каждую неделю, а не каждый день. Аргументация здесь такова: потери из-за не совсем правильных дневных позиций могут быть меньше, чем дополнительные издержки по сделкам для ежедневного изменения позиций. Вы должны определить, основываясь на используемой тор- говой стратегии, какие из потерь будут для вас меньше. Какой объем исторических данных необходим для расчета оптимальных портфелей? Этот вопрос можно сформулировать несколько иначе: «Какой объем исторических данных необходим для определения оптимального f данной рыночной системы?» Точного ответа не существует. Вообще, чем больше исторических данных вы используете, тем лучше должен быть результат (то есть оптимальные портфели в будущем будут напоминать нынешние оптимальные портфели, рассчитанные по историческим данным). Однако соотношения изменяются, хотя и медленно. Одна из проблем при использовании данных за слишком большой период времени заключается в том, что возникает тенденция к использованию в портфеле рынков, которые были активны в прошлом. Например, если бы вы создавали портфель в 1983 году на 5 годах прошлых данных, то, вероятнее всего, один из драгоценных металлов оказался бы частью оптимального портфеля. Однако торговые системы по драгоценным металлам работали в большинстве своем очень плохо на протяжении нескольких лет после 1980-1981 годов. Поэтому, как видите, при определении будущего оптимального портфеля между использованием слишком большого количества исторических данных и использованием слишком малого количества данных нужно найти золотую середину. И, наконец, возникает вопрос, как часто следует повторять всю процедуру поиска оптимального портфеля. По большому счету вы должны делать это постоянно. Однако в реальной жизни достаточно тестировать портфель каждые 3 месяца. И даже если производить эту операцию каждые 3 месяца, все еще есть высокая вероятность, что вы придете к тому же составу портфеля или очень сходному с тем, что создали ранее.
FXWizard
Гуру форума
Сумма весов систем в портфеле, превышающая 100%
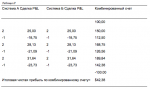
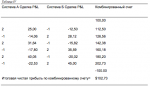
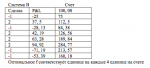
До настоящего момента мы ограничивали сумму процентных весов 100 про- центами. Однако возможно, что сумма процентных размещений для портфеля, который будет иметь наивысший геометрический рост, превысит 100%. Рас- смотрим, например, две рыночные системы, А и В, которые идентичны во всех отношениях, за тем исключением, что у них отрицательная корреляция (R < 0). Допустим, что оптимальное f в долларах для каждой из этих рыночных систем составляет 5000 долларов. Допустим, что оптимальный портфель на основе самого высокого среднего геометрического — это портфель, который размещает 50% в каждую из двух рыночных систем. Это означает, что вам следует торговать 1 контрактом на каждые 10 000 долларов баланса для рыночной системы А, и для системы В. Однако когда есть отрицательная корреляция, можно показать, что оптимальный рост счета в действительности будет достигнут при торговле 1 контрактом для баланса, меньшего 10 000 долларов для рыночной системы А и/или рыночной системы В. Другими словами, когда есть отрицательная корреляция, сумма процентных весов может превышать 100%. Более того, возможно, что процентные размещения в рыночные системы могут по отдельности превысить 100%.
Интересно рассмотреть случай, когда корреляция между двумя рыночными системами приближается к -1,00. В этом случае сумма для финансирования сделок по рыночным системам стремится стать бесконечно малой. Дело в том, что в таком портфеле почти не будет проигрышных дней, так как проигранная в данный день одной рыночной системой сумма возмещается суммой, выигранной другой
рыночной системой в тот же день. Поэтому с помощью диверсификации возможно получить оптимальный портфель, который размещает меньшую долю f (в долларах) в данную рыночную систему, чем при торговле только в этой рыночной системе. Для этого для каждой рыночной системы вы можете разделить оптимальное f в долларах на количество рыночных систем, в которых работаете. В нашем примере, вместо того чтобы выбрать 5000 долларов в качестве оптимального f для рыночной системы А, нам следует использовать 2500 долларов (разделив 5000 долларов, оптимальное f, на 2, количество рыночных систем, в которых мы собираемся торговать), и таким же образом следует поступить с рыночной системой В. Теперь, когда мы используем данную процедуру для определения оптимального среднего геометрического портфеля, который состоит из 50% для А и 50% для В, это означает, что нам следует торговать 1 контрактом на каждые 5000 долларов на балансе для рыночной системы А ($2500 / 0,5) и аналогично для В. В качестве еще одной рыночной системы вы можете использовать систему беспроцентного вклада. Это активы, не приносящие дохода, с HPR = 1,00 каждый день. Допустим, в нашем предыдущем примере оптимальный рост получен при 50% для системы А и 40% для системы В. Другими словами, следует торговать 1 контрактом на каждые 5000 долларов на балансе для рыночной системы А и 1 контрактом на каждые 6250 долларов для В ($2500 / 0,4). При использовании беспроцентного вклада в качестве другой рыночной системы это была бы одна из комбинаций (оптимальный портфель, который на 10% в деньгах). Если ваш портфель, найденный с помощью этой процедуры, не содержит систему беспроцентного вклада в качестве одной из составляющих, тогда вы должны повысить используемый фактор и разделить оптимальные f в долларах, используемые в качестве вводных данных. Возвращаясь к нашему примеру, допустим, мы использовали беспроцентный вклад и две рыночные системы, А и В. Далее предположим, что наш итоговый оптимальный портфель не содержит систему беспроцентного вклада. Пусть оптимальный портфель оказался на 60% в рыночной системе А, на 40% в рыночной системе В (возможна любая другая процентная комбинация, веса которой в сумме дают 100%) и на 0% в системе беспроцентного вклада. Если бы мы разделили наши оптимальные f в долларах на два, то этого было бы недостаточно. Мы должны разделить их на число, больше 2. Итак, мы вернемся и разделим наши оптимальные f в долларах на 3 или 4, пока не получим оптимальный портфель, который включает систему беспроцентного вклада. Конечно, в реальной жизни это не означает, что мы должны размещать какую-либо часть нашего торгового капитала в беспроцентные вклады. Беспроцентные активы стоит использовать для того, чтобы определить оптимальную сумму средств на 1 контракт в каждой рыночной системе при сравнении нескольких рыночных систем. Вы должны знать, что сумма процентных весов портфеля, при которых достигался наибольший геометрический рост в прошлом, может быть выше 100%. Этого можно достичь, разделив оптимальное f в долларах для каждой рыночной системы на некое целое число (которое обычно является числом рыночных систем), включив беспроцентный вклад (то есть рыночную систему с HPR = 1,00 каждый день) в качестве еще одной рыночной системы. Корреляции различных рыночных систем могут оказать серьезное воздействие на портфель. Важно понимать, что портфель может быть больше, чем сумма его частей (если корреляции его составляющих частей достаточно низки). Также возможно, что портфель будет меньше, чем сумма его частей (если корреляции слишком высоки). Рассмотрим снова игру с броском монеты, где вы выигрываете 2 доллара, когда выпадает лицевая сторона, и проигрываете 1 доллар, когда выпадает обратная сторона. Каждый бросок имеет математическое ожидание (арифметическое) пятьдесят центов. Оптимальное f составляет 0,25, то есть надо ставить 1 доллар на каждые 4 доллара на счете, а среднее геометрическое составляет 1,0607. Теперь рассмотрим вторую игру, где сумма, которую вы можете выиграть при броске монеты, составляет 0,90 долларов, а сумма, которую вы можете проиграть, — 1,10 долларов. Такая игра имеет отрицательное математическое ожидание -0,10 доллара, таким образом, здесь нет оптимального f и соответственно нет и среднего геометрического. Посмотрим, что произойдет, когда мы будем играть в обе игры одновременно. Если корреляция этих игр равна 1,0 (то есть мы выигрываем при выпадении лицевой стороны, а монеты всегда падают либо на лицевые стороны, либо на обратные стороны), тогда результаты были бы следующими: мы выигрываем 2,90 доллара при выпадении лицевой стороны или проигрываем 2,10 доллара при выпадении обратной. Такая игра имеет математическое ожидание 0,40 доллара, оптимальное f= 0,14 и среднее геометрическое 1,013. Очевидно, что это худший подход к торговле с положительным математическим ожиданием. Теперь допустим, что игры имеют отрицательную корреляцию. То есть, когда монета в игре с положительным математическим ожиданием выпадает на лицевую сторону, мы теряем 1,10 доллара в игре с отрицательным ожиданием, и наоборот. Таким образом, результатом двух игр будет выигрыш 0,90 доллара в одном случае и проигрыш -0,10 доллара в другом случае. Математическое ожидание все еще 0,40 доллара, однако оптимальное f= 0,44, что дает среднее геометрическое 1,67. Вспомните, что среднее геометрическое является фактором роста вашего счета в среднем за одну игру.. Это означает, что в такой игре в среднем можно ожидать выигрыша в 10 раз больше, чем в уже рассмотренной одиночной игре с положительным математическим ожиданием. Однако этот результат получен с помощью игры с положительным математическим ожиданием и ее комбинирования с игрой с отрицательным ожиданием. Причина большой разницы в результатах возникает из-за отрицательной корреляции между двумя рыночными системами. Мы рассмотрели пример, когда портфель больше, чем сумма его частей.
Важно помнить, что исторически ваш проигрыш может быть такой же большой, как и процент f (в смысле возможного уменьшения баланса). В действительности вам следует ожидать, что в будущем он будет выше, чем данное значение. Это означает, что комбинация двух рыночных систем, даже если они имеют отрицательную корреляцию, может привести к уменьшению баланса на 44%. Это больше, чем в системе с положительным математическим ожиданием, в которой оптимальное f= 0,25, и поэтому максимальный исторический проигрыш уменьшит баланс только на 25%. Мораль такова: диверсификация, если она произведена правильно, является методом, который повышает прибыли. Она не обязательно уменьшает проигрыши худшего случая, что абсолютно противоречит популярному представлению. Диверсификация смягчает многие мелкие проигрыши, но она не уменьшает проигрыши худшего случая. При оптимальном f максимальные проигрыши могут быть существенно больше, чем думают многие. Поэтому, даже если вы хорошо диверсифицировали портфель, следует быть готовым к значительным уменьшениям баланса. Однако давайте вернемся и посмотрим на результаты, когда коэффициент корреляции между двумя играми равен 0. В такой ситуации, какими бы ни были результаты одного броска, они не влияют на результаты другого броска. Таким образом, есть четыре возможных результата:

Математическое ожидание равно:
МО = 2,9 * 0,25 + 0,9 * 0,25 - 0,1 * 0,25 - 2,1 * 0,25 = 0,725 + 0,225 - 0,025 - 0,525
=0,4
Математическое ожидание равно 0,40 доллара. Оптимальное f в этой последовательности составляет 0,26, или 1 ставка на каждые 8,08 доллара на балансе счета (так как наибольший проигрыш здесь равен -2,10 доллара). Таким образом, максимальный исторический проигрыш может быть 26% (примерно такой же, что и в простой игре с положительным математическим ожиданием). Однако в этом примере происходит сглаживание уменьшении баланса. Если бы мы просто рассматривали игру с положительным ожиданием, то третья последовательность принесла бы нам максимальный проигрыш. Так как мы комбинируем две системы, третья последовательность более ровная. Это единственный плюс. Среднее геометрическое здесь равно 1,025, то есть скорость роста в два раза меньше, чем при простой игре с положительным математическим ожиданием. Мы делаем 4 ставки (когда могли бы сделать только 2 ставки в простой игре с положительным ожиданием), а больше не зарабатываем:
1,0607^2= 1,12508449 1,025^4= 1,103812891
Очевидно, что при диверсификации вы должны использовать такие рыночные системы, которые имеют самую низкую корреляцию прибылей друг к другу, и желательно отрицательную корреляцию. Вы должны понимать, что уменьшение баланса худшего случая едва ли будет смягчено диверсификацией, хотя вы сможете смягчать многие более слабые уменьшения баланса. Наибольшая польза диверсификации состоит в улучшении среднего геометрического. Метод поиска оптимального портфеля путем рассмотрения чистых дневных HPR упраздняет необходимость смотреть за тем, сколько сделок в каждой рыночной системе произошло. Использование этого метода позволит вам наблюдать только за средним геометрическим независимо от частоты сделок. Таким образом, среднее геометрическое становится единственной статистической оценкой того, насколько прибыльным является портфель. Главная цель диверсификации — это получение наивысшего среднего геометрического.
До настоящего момента мы ограничивали сумму процентных весов 100 про- центами. Однако возможно, что сумма процентных размещений для портфеля, который будет иметь наивысший геометрический рост, превысит 100%. Рас- смотрим, например, две рыночные системы, А и В, которые идентичны во всех отношениях, за тем исключением, что у них отрицательная корреляция (R < 0). Допустим, что оптимальное f в долларах для каждой из этих рыночных систем составляет 5000 долларов. Допустим, что оптимальный портфель на основе самого высокого среднего геометрического — это портфель, который размещает 50% в каждую из двух рыночных систем. Это означает, что вам следует торговать 1 контрактом на каждые 10 000 долларов баланса для рыночной системы А, и для системы В. Однако когда есть отрицательная корреляция, можно показать, что оптимальный рост счета в действительности будет достигнут при торговле 1 контрактом для баланса, меньшего 10 000 долларов для рыночной системы А и/или рыночной системы В. Другими словами, когда есть отрицательная корреляция, сумма процентных весов может превышать 100%. Более того, возможно, что процентные размещения в рыночные системы могут по отдельности превысить 100%.
Интересно рассмотреть случай, когда корреляция между двумя рыночными системами приближается к -1,00. В этом случае сумма для финансирования сделок по рыночным системам стремится стать бесконечно малой. Дело в том, что в таком портфеле почти не будет проигрышных дней, так как проигранная в данный день одной рыночной системой сумма возмещается суммой, выигранной другой
рыночной системой в тот же день. Поэтому с помощью диверсификации возможно получить оптимальный портфель, который размещает меньшую долю f (в долларах) в данную рыночную систему, чем при торговле только в этой рыночной системе. Для этого для каждой рыночной системы вы можете разделить оптимальное f в долларах на количество рыночных систем, в которых работаете. В нашем примере, вместо того чтобы выбрать 5000 долларов в качестве оптимального f для рыночной системы А, нам следует использовать 2500 долларов (разделив 5000 долларов, оптимальное f, на 2, количество рыночных систем, в которых мы собираемся торговать), и таким же образом следует поступить с рыночной системой В. Теперь, когда мы используем данную процедуру для определения оптимального среднего геометрического портфеля, который состоит из 50% для А и 50% для В, это означает, что нам следует торговать 1 контрактом на каждые 5000 долларов на балансе для рыночной системы А ($2500 / 0,5) и аналогично для В. В качестве еще одной рыночной системы вы можете использовать систему беспроцентного вклада. Это активы, не приносящие дохода, с HPR = 1,00 каждый день. Допустим, в нашем предыдущем примере оптимальный рост получен при 50% для системы А и 40% для системы В. Другими словами, следует торговать 1 контрактом на каждые 5000 долларов на балансе для рыночной системы А и 1 контрактом на каждые 6250 долларов для В ($2500 / 0,4). При использовании беспроцентного вклада в качестве другой рыночной системы это была бы одна из комбинаций (оптимальный портфель, который на 10% в деньгах). Если ваш портфель, найденный с помощью этой процедуры, не содержит систему беспроцентного вклада в качестве одной из составляющих, тогда вы должны повысить используемый фактор и разделить оптимальные f в долларах, используемые в качестве вводных данных. Возвращаясь к нашему примеру, допустим, мы использовали беспроцентный вклад и две рыночные системы, А и В. Далее предположим, что наш итоговый оптимальный портфель не содержит систему беспроцентного вклада. Пусть оптимальный портфель оказался на 60% в рыночной системе А, на 40% в рыночной системе В (возможна любая другая процентная комбинация, веса которой в сумме дают 100%) и на 0% в системе беспроцентного вклада. Если бы мы разделили наши оптимальные f в долларах на два, то этого было бы недостаточно. Мы должны разделить их на число, больше 2. Итак, мы вернемся и разделим наши оптимальные f в долларах на 3 или 4, пока не получим оптимальный портфель, который включает систему беспроцентного вклада. Конечно, в реальной жизни это не означает, что мы должны размещать какую-либо часть нашего торгового капитала в беспроцентные вклады. Беспроцентные активы стоит использовать для того, чтобы определить оптимальную сумму средств на 1 контракт в каждой рыночной системе при сравнении нескольких рыночных систем. Вы должны знать, что сумма процентных весов портфеля, при которых достигался наибольший геометрический рост в прошлом, может быть выше 100%. Этого можно достичь, разделив оптимальное f в долларах для каждой рыночной системы на некое целое число (которое обычно является числом рыночных систем), включив беспроцентный вклад (то есть рыночную систему с HPR = 1,00 каждый день) в качестве еще одной рыночной системы. Корреляции различных рыночных систем могут оказать серьезное воздействие на портфель. Важно понимать, что портфель может быть больше, чем сумма его частей (если корреляции его составляющих частей достаточно низки). Также возможно, что портфель будет меньше, чем сумма его частей (если корреляции слишком высоки). Рассмотрим снова игру с броском монеты, где вы выигрываете 2 доллара, когда выпадает лицевая сторона, и проигрываете 1 доллар, когда выпадает обратная сторона. Каждый бросок имеет математическое ожидание (арифметическое) пятьдесят центов. Оптимальное f составляет 0,25, то есть надо ставить 1 доллар на каждые 4 доллара на счете, а среднее геометрическое составляет 1,0607. Теперь рассмотрим вторую игру, где сумма, которую вы можете выиграть при броске монеты, составляет 0,90 долларов, а сумма, которую вы можете проиграть, — 1,10 долларов. Такая игра имеет отрицательное математическое ожидание -0,10 доллара, таким образом, здесь нет оптимального f и соответственно нет и среднего геометрического. Посмотрим, что произойдет, когда мы будем играть в обе игры одновременно. Если корреляция этих игр равна 1,0 (то есть мы выигрываем при выпадении лицевой стороны, а монеты всегда падают либо на лицевые стороны, либо на обратные стороны), тогда результаты были бы следующими: мы выигрываем 2,90 доллара при выпадении лицевой стороны или проигрываем 2,10 доллара при выпадении обратной. Такая игра имеет математическое ожидание 0,40 доллара, оптимальное f= 0,14 и среднее геометрическое 1,013. Очевидно, что это худший подход к торговле с положительным математическим ожиданием. Теперь допустим, что игры имеют отрицательную корреляцию. То есть, когда монета в игре с положительным математическим ожиданием выпадает на лицевую сторону, мы теряем 1,10 доллара в игре с отрицательным ожиданием, и наоборот. Таким образом, результатом двух игр будет выигрыш 0,90 доллара в одном случае и проигрыш -0,10 доллара в другом случае. Математическое ожидание все еще 0,40 доллара, однако оптимальное f= 0,44, что дает среднее геометрическое 1,67. Вспомните, что среднее геометрическое является фактором роста вашего счета в среднем за одну игру.. Это означает, что в такой игре в среднем можно ожидать выигрыша в 10 раз больше, чем в уже рассмотренной одиночной игре с положительным математическим ожиданием. Однако этот результат получен с помощью игры с положительным математическим ожиданием и ее комбинирования с игрой с отрицательным ожиданием. Причина большой разницы в результатах возникает из-за отрицательной корреляции между двумя рыночными системами. Мы рассмотрели пример, когда портфель больше, чем сумма его частей.
Важно помнить, что исторически ваш проигрыш может быть такой же большой, как и процент f (в смысле возможного уменьшения баланса). В действительности вам следует ожидать, что в будущем он будет выше, чем данное значение. Это означает, что комбинация двух рыночных систем, даже если они имеют отрицательную корреляцию, может привести к уменьшению баланса на 44%. Это больше, чем в системе с положительным математическим ожиданием, в которой оптимальное f= 0,25, и поэтому максимальный исторический проигрыш уменьшит баланс только на 25%. Мораль такова: диверсификация, если она произведена правильно, является методом, который повышает прибыли. Она не обязательно уменьшает проигрыши худшего случая, что абсолютно противоречит популярному представлению. Диверсификация смягчает многие мелкие проигрыши, но она не уменьшает проигрыши худшего случая. При оптимальном f максимальные проигрыши могут быть существенно больше, чем думают многие. Поэтому, даже если вы хорошо диверсифицировали портфель, следует быть готовым к значительным уменьшениям баланса. Однако давайте вернемся и посмотрим на результаты, когда коэффициент корреляции между двумя играми равен 0. В такой ситуации, какими бы ни были результаты одного броска, они не влияют на результаты другого броска. Таким образом, есть четыре возможных результата:
Математическое ожидание равно:
МО = 2,9 * 0,25 + 0,9 * 0,25 - 0,1 * 0,25 - 2,1 * 0,25 = 0,725 + 0,225 - 0,025 - 0,525
=0,4
Математическое ожидание равно 0,40 доллара. Оптимальное f в этой последовательности составляет 0,26, или 1 ставка на каждые 8,08 доллара на балансе счета (так как наибольший проигрыш здесь равен -2,10 доллара). Таким образом, максимальный исторический проигрыш может быть 26% (примерно такой же, что и в простой игре с положительным математическим ожиданием). Однако в этом примере происходит сглаживание уменьшении баланса. Если бы мы просто рассматривали игру с положительным ожиданием, то третья последовательность принесла бы нам максимальный проигрыш. Так как мы комбинируем две системы, третья последовательность более ровная. Это единственный плюс. Среднее геометрическое здесь равно 1,025, то есть скорость роста в два раза меньше, чем при простой игре с положительным математическим ожиданием. Мы делаем 4 ставки (когда могли бы сделать только 2 ставки в простой игре с положительным ожиданием), а больше не зарабатываем:
1,0607^2= 1,12508449 1,025^4= 1,103812891
Очевидно, что при диверсификации вы должны использовать такие рыночные системы, которые имеют самую низкую корреляцию прибылей друг к другу, и желательно отрицательную корреляцию. Вы должны понимать, что уменьшение баланса худшего случая едва ли будет смягчено диверсификацией, хотя вы сможете смягчать многие более слабые уменьшения баланса. Наибольшая польза диверсификации состоит в улучшении среднего геометрического. Метод поиска оптимального портфеля путем рассмотрения чистых дневных HPR упраздняет необходимость смотреть за тем, сколько сделок в каждой рыночной системе произошло. Использование этого метода позволит вам наблюдать только за средним геометрическим независимо от частоты сделок. Таким образом, среднее геометрическое становится единственной статистической оценкой того, насколько прибыльным является портфель. Главная цель диверсификации — это получение наивысшего среднего геометрического.
Вложения
FXWizard
Гуру форума
Как разброс результатов затрагивает геометрический рост
После того как мы признали тот факт, что, хотим мы того или нет, сознательно или нет, количество для торговли определяется по уровню баланса на счете, можно рассматривать HPR, а не денежные суммы. Таким образом, мы придадим управлению деньгами определенность и точность. Мы сможем проверить наши стратегии управления деньгами, составить правила и сделать определенные выводы. Посмотрим, как связан геометрический рост и разброс результатов (HPR).
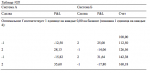
В этой дискуссии мы для простоты будем использовать пример азартной игры. Рассмотрим две системы: систему А, которая выигрывает 10% времени и имеет отношение выигрыш/проигрыш 28 к 1, и систему В, которая выигрывает 70% времени и имеет отношение выигрыш/проигрыш 1,9 к 1. Наше математическое ожидание на единицу ставки для А равно 1,9, а для В равно 0,4. Поэтому мы мо-
жем сказать, что для каждой единицы ставки система А выиграет, в среднем, в 4,75 раз больше, чем система В. Но давайте рассмотрим торговлю фиксированной долей. Мы можем найти оптимальные f, разделив математическое ожидание на отношение выигрыш/проигрыш. Это даст нам оптимальное f = 0,0678 для А и 0,4 для В. Средние геометрические для каждой системы при соответствующих значениях оптимальных f составят:
А= 1,044176755
В= 1,0857629
Как видите, система В, несмотря на то что ее математическое ожидание примерно в четыре раза меньше, чем системы А, приносит почти в два раза больше за ставку (доходность 8,57629% за ставку, когда вы реинвестируете с оптимальным f), чем система А (которая приносит 4,4176755% за ставку, когда вы реинвестируете с оптимальным f).

Проигрыш 50% по балансу потребует 100% прибыли для возмещения; 1,044177 в степени Х будет равно 2,0, когда Х приблизительно равно 16,5, то есть для возмещения 50% проигрыша для системы А потребуется более 16 сделок. Сравним с системой В, где 1,0857629 в степени Х будет равно 2,0, когда Х приблизительно равно 9, то есть для системы В потребуется 9 сделок для возмещения 50% проигрыша.
В чем здесь дело? Не потому ли все это происходит, что система В имеет процент выигрышных сделок выше? Истинная причина, по которой В функционирует лучше А, кроется в разбросе результатов и его влиянии на функцию роста. Большинство трейдеров ошибочно считают, что функция роста TWR задается следующим образом:

где R = процентная ставка за период (например, 7% = 0,07);
N = количество периодов.
Так как 1 + R то же, что и HPR, большинство ошибочно полагает, что функция роста1 TWR равна:

Эта функция верна только тогда, когда прибыль (то есть HPR) постоянна, чего в торговле не бывает. Реальная функция роста в торговле (или любой другой среде,
1 Многие ошибочно используют среднее арифметическое HPR в уравнении HPR ^ N. Как здесь показано, это не даст истинное TWR после N игр. Вы должны использовать геометрическое, а не арифметическое среднее HPR ^ N. Это даст истинное TWR. Если стандартное отклонение HPR равно 0, тогда арифметическое среднее HPR и геометрическое среднее HPR эквивалентны, и не имеет значения, какое из них вы используете.

где HPR не является постоянной) — это произведение всех HPR. Допустим, мы торгуем кофе, наше оптимальное f составляет 1 контракт на каждую 21 000 долларов на балансе счета и прошло 2 сделки, одна из которых принесла убыток 210 долларов, а другая выигрыш 210 долларов. В этом примере HPR равны 0,99 и 1,01 соответственно. Таким образом, TWR равно:
TWR = 1,01 * 0,99 = 0,9999
Дополнительную информацию можно получить, используя оценочное среднее геометрическое (EGM):

или

Теперь возведем уравнение (1.16а) или (1.166) в степень N, чтобы рассчитать TWR Оно будет близко к «мультипликативной» функции роста, действительному TWR

или

где N = количество периодов; АНPR = среднее арифметическое HPR;
SD = стандартное отклонение значений HPR; V = дисперсия значений HPR.
Оба уравнения (1.19) эквивалентны.
Полученная информация говорит, что найден компромисс между увеличением средней арифметической торговли (HPR) и дисперсией HPR, и становится ясна причина, по которой система (1,9:1 ; 70%) работает лучше, чем система (28:1; 10%)!
Нашей целью является максимизация коэффициента этой функции, т.е. мак- симизация следующей величины:

Показатель оценочного TWR, т.е. N, сам о себе позаботится. Увеличение N не яв- ляется проблемой, так как мы можем расширить количество рынков или торговать в более краткосрочных типах систем.
Расчет дисперсии и стандартного отклонения (V и SD соответственно) может оказаться трудным для большинства людей, не знакомых со статистикой. Вместо этих величин многие используют среднее абсолютное отклонение, которое мы на- зовем М. Чтобы найти М, надо просто взять среднее абсолютное значение разно-сти самой величины и ее среднего значения.
После того как мы признали тот факт, что, хотим мы того или нет, сознательно или нет, количество для торговли определяется по уровню баланса на счете, можно рассматривать HPR, а не денежные суммы. Таким образом, мы придадим управлению деньгами определенность и точность. Мы сможем проверить наши стратегии управления деньгами, составить правила и сделать определенные выводы. Посмотрим, как связан геометрический рост и разброс результатов (HPR).
В этой дискуссии мы для простоты будем использовать пример азартной игры. Рассмотрим две системы: систему А, которая выигрывает 10% времени и имеет отношение выигрыш/проигрыш 28 к 1, и систему В, которая выигрывает 70% времени и имеет отношение выигрыш/проигрыш 1,9 к 1. Наше математическое ожидание на единицу ставки для А равно 1,9, а для В равно 0,4. Поэтому мы мо-
жем сказать, что для каждой единицы ставки система А выиграет, в среднем, в 4,75 раз больше, чем система В. Но давайте рассмотрим торговлю фиксированной долей. Мы можем найти оптимальные f, разделив математическое ожидание на отношение выигрыш/проигрыш. Это даст нам оптимальное f = 0,0678 для А и 0,4 для В. Средние геометрические для каждой системы при соответствующих значениях оптимальных f составят:
А= 1,044176755
В= 1,0857629
Как видите, система В, несмотря на то что ее математическое ожидание примерно в четыре раза меньше, чем системы А, приносит почти в два раза больше за ставку (доходность 8,57629% за ставку, когда вы реинвестируете с оптимальным f), чем система А (которая приносит 4,4176755% за ставку, когда вы реинвестируете с оптимальным f).
Проигрыш 50% по балансу потребует 100% прибыли для возмещения; 1,044177 в степени Х будет равно 2,0, когда Х приблизительно равно 16,5, то есть для возмещения 50% проигрыша для системы А потребуется более 16 сделок. Сравним с системой В, где 1,0857629 в степени Х будет равно 2,0, когда Х приблизительно равно 9, то есть для системы В потребуется 9 сделок для возмещения 50% проигрыша.
В чем здесь дело? Не потому ли все это происходит, что система В имеет процент выигрышных сделок выше? Истинная причина, по которой В функционирует лучше А, кроется в разбросе результатов и его влиянии на функцию роста. Большинство трейдеров ошибочно считают, что функция роста TWR задается следующим образом:
где R = процентная ставка за период (например, 7% = 0,07);
N = количество периодов.
Так как 1 + R то же, что и HPR, большинство ошибочно полагает, что функция роста1 TWR равна:
Эта функция верна только тогда, когда прибыль (то есть HPR) постоянна, чего в торговле не бывает. Реальная функция роста в торговле (или любой другой среде,
1 Многие ошибочно используют среднее арифметическое HPR в уравнении HPR ^ N. Как здесь показано, это не даст истинное TWR после N игр. Вы должны использовать геометрическое, а не арифметическое среднее HPR ^ N. Это даст истинное TWR. Если стандартное отклонение HPR равно 0, тогда арифметическое среднее HPR и геометрическое среднее HPR эквивалентны, и не имеет значения, какое из них вы используете.

где HPR не является постоянной) — это произведение всех HPR. Допустим, мы торгуем кофе, наше оптимальное f составляет 1 контракт на каждую 21 000 долларов на балансе счета и прошло 2 сделки, одна из которых принесла убыток 210 долларов, а другая выигрыш 210 долларов. В этом примере HPR равны 0,99 и 1,01 соответственно. Таким образом, TWR равно:
TWR = 1,01 * 0,99 = 0,9999
Дополнительную информацию можно получить, используя оценочное среднее геометрическое (EGM):
или
Теперь возведем уравнение (1.16а) или (1.166) в степень N, чтобы рассчитать TWR Оно будет близко к «мультипликативной» функции роста, действительному TWR
или
где N = количество периодов; АНPR = среднее арифметическое HPR;
SD = стандартное отклонение значений HPR; V = дисперсия значений HPR.
Оба уравнения (1.19) эквивалентны.
Полученная информация говорит, что найден компромисс между увеличением средней арифметической торговли (HPR) и дисперсией HPR, и становится ясна причина, по которой система (1,9:1 ; 70%) работает лучше, чем система (28:1; 10%)!
Нашей целью является максимизация коэффициента этой функции, т.е. мак- симизация следующей величины:
Показатель оценочного TWR, т.е. N, сам о себе позаботится. Увеличение N не яв- ляется проблемой, так как мы можем расширить количество рынков или торговать в более краткосрочных типах систем.
Расчет дисперсии и стандартного отклонения (V и SD соответственно) может оказаться трудным для большинства людей, не знакомых со статистикой. Вместо этих величин многие используют среднее абсолютное отклонение, которое мы на- зовем М. Чтобы найти М, надо просто взять среднее абсолютное значение разно-сти самой величины и ее среднего значения.
Вложения
FXWizard
Гуру форума
При колоколообразном распределении (как почти всегда бывает с распределением прибылей и убытков торговой системы) среднее абсолютное отклонение примерно равно 0,8 стандартного отклонения (в нормальном распределении оно составляет 0,7979). Поэтому мы можем сказать:
и
Обозначим среднее арифметическое HPR переменной А, а среднее геометрическое HPR переменной G. Используя уравнение (1.166), мы можем выразить оценочное среднее геометрическое следующим образом:
Из этого уравнения получим:
Теперь вместо дисперсии подставим стандартное отклонение [как в (1.16а)]:
Из этого уравнения мы можем выделить каждую переменную, а также выделить ноль, чтобы получить фундаментальные соотношения между средним арифметическим, средним геометрическим и разбросом, выраженным здесь как SD ^ 2:
В этих уравнениях значение SD^2 можно записать как V или как (1,25 * М) ^2. Это подводит нас к той точке, когда мы можем описать существующие взаимосвязи. Отметьте, что последнее из уравнений — это теорема Пифагора: сумма квадратов катетов равна квадрату гипотенузы! Но здесь гипотенуза это А, а мы хотим максимизировать одну из ее сторон, G. При увеличении G любое повышение D («катет» дисперсии, равный SD или V^(1/2), или 1,25 * М) приведет к увеличению А. Когда D равно нулю, тогда А равно G, этим самым соответствуя ложно толкуемой функции роста TWR = (1 + R)^ N. Действительно, когда D равно нулю, тогда А равно G в соответствии с уравнением (1.26).
Мы можем сказать, что повышение А^ 2 оказывает на G то же воздействие, что и аналогичное понижение величины (1,25 * М) ^ 2.
Вложения
FXWizard
Гуру форума
Чтобы понять это, рассмотрим изменение А от 1,1 до 1,2:

Когда A=l,l,ToSD=0,l. Когда А = 1,2, то, чтобы получить эквивалентное G, SD должно быть равно 0,4899, согласно уравнению (1.27). Так как М = = 0,8 *
SD,ToM=0,3919. Если мы возведем в квадрат значения А и SD и рассчитаем разность, то получим 0,23 в соответствии с уравнением (1.29). Рассмотрим следующую таблицу:

Отметьте, что в предыдущем примере, где мы начали с меньших значений разброса (SD или М), требовалось их большее повышение, чтобы достичь того же G. Таким образом, можно утверждать, что чем сильнее вы уменьшаете дисперсию, тем легче дается больший выигрыш. Это экспоненциальная функция, причем в пределе, при нулевой дисперсии, G равно А. Трейдер, который торгует на фиксированной долевой основе, должен максимизировать G, но не обязательно А. При максимизации G надо понимать, что стандартное отклонение SD затрагивает G в той же степени, что и А в соответствии с теоремой Пифагора! Таким образом, когда трейдер уменьшает стандартное отклонение (SD) своих сделок, это эквивалентно повышению арифметического среднего HPR (т.е. А), и наоборот!
Когда A=l,l,ToSD=0,l. Когда А = 1,2, то, чтобы получить эквивалентное G, SD должно быть равно 0,4899, согласно уравнению (1.27). Так как М = = 0,8 *
SD,ToM=0,3919. Если мы возведем в квадрат значения А и SD и рассчитаем разность, то получим 0,23 в соответствии с уравнением (1.29). Рассмотрим следующую таблицу:
Отметьте, что в предыдущем примере, где мы начали с меньших значений разброса (SD или М), требовалось их большее повышение, чтобы достичь того же G. Таким образом, можно утверждать, что чем сильнее вы уменьшаете дисперсию, тем легче дается больший выигрыш. Это экспоненциальная функция, причем в пределе, при нулевой дисперсии, G равно А. Трейдер, который торгует на фиксированной долевой основе, должен максимизировать G, но не обязательно А. При максимизации G надо понимать, что стандартное отклонение SD затрагивает G в той же степени, что и А в соответствии с теоремой Пифагора! Таким образом, когда трейдер уменьшает стандартное отклонение (SD) своих сделок, это эквивалентно повышению арифметического среднего HPR (т.е. А), и наоборот!
Вложения
FXWizard
Гуру форума
Фундаментальное уравнение торговли
Мы можем получить гораздо больше, чем просто понимание того факта, что уменьшение размера проигрышей улучшает конечный результат. Вернемся к уравнению (1.19а):

Подставим А вместо AHPR (среднее арифметическое HPR). Далее, так как (X ^Y) ^ Z = Х ^ (Y * Z), мы можем еще больше упростить уравнение:

Это последнее уравнение мы назовем фундаментальным уравнением торговли, так как оно описывает, как различные факторы: А, SD и N — влияют на результат торговли. Очевидны несколько фактов. Во-первых, если А меньше или равно единице, тогда при любых значениях двух других переменных, SD и N, наш результат не может быть больше единицы. Если А меньше единицы, то при N, стремящемся к бесконечности, наш результат приближается к нулю. Это означает, что, если А меньше или равно 1 (математическое ожидание меньше или равно нулю, так как математическое ожидание равно А - 1), у нас нет шансов получить прибыль. Фактически, если А меньше 1, то наше разорение — это просто вопрос времени (то есть достаточно большого N).
При условии, что А больше 1, сростом N увеличивается наша прибыль. Например, система показала среднее арифметическое 1,1 и стандартное отклонение 0,25. Таким образом:

В нашем примере, где коэффициент равен 1,1475; 1,1475 ^ (1/2) = 1,071214264. Таким образом, каждая следующая сделка, каждое увеличение N на единицу

соответствует умножению нашего конечного счета на 1,071214264. Отметьте, что это число является средним геометрическим. Каждый раз, когда осуществляется сделка и когда N увеличивается на единицу, коэффициент умножается на среднее геометрическое. В этом и состоит действительная польза диверсификации, выраженная математически фундаментальным уравнением торговли. Диверсификация позволяет вам как бы увеличить N (т.е. количество сделок) за определенный период времени. Есть еще одна важная деталь, которую необходимо отметить при рассмотрении фундаментального уравнения торговли: хорошо, когда вы уменьшаете стандартное отклонение больше, чем арифметическое среднее HPR. Поэтому следует быстро закрывать убыточные позиции (использовать маленький stop-loss). Но уравнение также демонстрирует, что при выборе слишком жесткого стопа вы можете больше потерять. Вас выбьет с рынка из-за слишком большого количества сделок с маленьким проигрышем, которые позднее оказались бы прибыльными, поскольку А уменьшается в большей степени, чем SD. Вместе с тем, и уменьшение больших выигрышных сделок поможет вашей системе, если это уменьшает SD больше, чем уменьшает А. Во многих случаях этого можно достичь путем включения в вашу торговую программу опционов. Позиция по опционам, которая направлена против позиции базового инструмента (покупка опциона или продажа соответствующего опциона), может оказаться весьма полезной. Например, если у вас длинная позиция по какой-либо акции (или товару), покупка пут-опциона (или продажа колл-опциона) может уменьшить ваше SD по совокупной позиции в большей степени, чем уменьшить А. Если вы получаете прибыль по базовому инструменту, то будете в убытке по опциону. При этом убыток опциону лишь незначительно уменьшит общую прибыль. Таким образом, вы уменьшили как ваше SD, так и А. Если вы не получаете прибыль по базовому инструменту, вам надо увеличить А и уменьшить SD. Надо стремиться уменьшить SD в большей степени, чем уменьшить А.
Конечно, издержки на трансакции при такой стратегии довольно значительны, и они всегда должны приниматься в расчет. Чтобы воспользоваться такой стратегией, ваша программа не должна быть ориентирована на очень короткий срок. Все вышесказанное лишь подтверждает, что различные стратегии и различные торговые правила должны рассматриваться сточки зрения фундаментального уравнения торговли. Таким образом, мы можем оценить влияние этих факторов на уровень возможных убытков и понять, что именно необходимо сделать для улучшения системы.
Допустим, в долгосрочной торговой программе была использована выше- упомянутая стратегия покупки пут-опциона совместно с длинной позицией по базовому инструменту, в результате мы получили большее оценочное TWR. Ситуация, когда одновременно открыты длинная позиция по базовому инструменту и позиция по пут-опциону, эквивалентна просто длинной позиции по колл-опциону. В том случае лучше просто купить колл-опцион, так как издержки на трансакции будут существенно ниже1, чем при наличии длинной позиции по базовому инструменту и длинной позиции по пут-опциону. Продемонстрируем это на примере рынка индексов акций в 1987 году. Допустим, мы покупаем базовый инструмент — индекс ОЕХ. Система, которую мы будем использовать, является простым 20-дневным прорывом канала. Каждый день мы рассчитываем самый высокий максимум и самый низкий минимум последних 20 дней. Затем, в течение дня, если рынок повышается и касается верхней точки, мы покупаем. Если цены идут вниз и касаются низшей точки, мы продаем. Если дневные открытия выше или ниже точек входа в рынок, мы входим при открытии. Такая система подразумевает постоянную торговлю на рынке:
1 Здесь есть еще один плюс, который сразу может быть и не виден. Он состоит в том, что мы заранее знаем проигрыш худшего случая. Учитывая, насколько чувствительно уравнение оптимального f к наибольшему проигрышу, такая стратегия может приблизить нас к пику кривой f и показать, каким может быть наибольший проигрыш. Во-вторых, проблема проигрыша в 3 стандартных отклонениях (или больше) с более высокой вероятностью, чем подразумевает нормальное распределение, будет устранена. Именно гигантские проигрыши более 3 стандартных отклонений разоряют большинство трейдеров. Опционные стратегии могут полностью упразднить такие проигрыши.

Если определять оптимальное
ветствующее среднее геометрическое (фактор роста на нашем счете за игру) равно 1,12445.
Теперь мы возьмем те же сделки, только будем использовать модель оценки фондовых опционов Блэка-Шоулса (подробно об этом будет рассказано в главе 5), и преобразуем входные цены в теоретические цены опционов. Входные данные для ценовой модели будут следующими: историческая волатильность, рассчитанная на основе 20 дней (расчет исторической волатильности также приводится в главе 5), безрисковая ставка 6% и 260,8875 дней (это среднее число рабочих дней в году). Далее мы допустим, что покупаем опционы, когда остается ровно 0,5 года до даты их исполнения (6 месяцев), и что они «при деньгах». Другими словами, существуют цены исполнения, в точности соответствующие цене входа на рынок. Покупка коллопциона, когда система в длинной позиции по базовому инструменту, и пут-опциона, когда система в короткой позиции по базовому инструменту, с учетом параметров упомянутой модели оценки опционов, даст в результате следующий поток сделок:

Если рассчитать оптимальное f по этому потоку сделок, мы придем к выводу, что соответствующее среднее геометрическое (фактор роста на нашем счете за игру) равно 1,2166. Сравните его со средним геометрическим при оптимальном f для базового инструмента 1,12445. Разница огромная. Так как мы получили всего б сделок, то можно возвести каждое среднее геометрическое в 6-ую степень для определения TWR. Это даст TWR по базовому инструменту 2,02 против TWR по опционам 3,24. Преобразуем TWR в процент прибыли от нашего начального счета. Мы получим 102% прибыли при торговле по базовому инструменту и 224% прибыли при торговле опционами. Опционы в рассмотренном случае предпочтительнее, что подтверждается фундаментальным уравнением торговли.
Длинные позиции по опционам могут быть менее эффективными, чем длинные позиции по базовому инструменту. Чтобы не сделать здесь ошибку, торговые стратегии (а также выбор серии опционов) необходимо рассматривать с точки зрения фундаментального уравнения торговли.
Как видите, фундаментальное уравнение торговли можно использовать для улучшения торговли. Улучшения могут заключаться в изменении жесткости при- казов на закрытие убыточных позиций (stop-loss приказов), в установлении целей и так далее. Эти изменения могут быть вызваны неэффективностью текущей тор- говли, а также неэффективностью торговой методологии.
Надеюсь, вы теперь понимаете, что компьютер неверно используется большин- ством трейдеров. Оптимизация, поиск систем и значений параметров, которые бы заработали больше всего денег на прошлых данных,— по сути пустая трата времени. Вам надо получить систему, которая будет прибыльна в будущем. С помощью грамотного управления капиталом вы сможете «выжать» максимум из системы, которая лишь минимально прибыльна. Прибыльность системы в большей степени определяется управлением капиталом, которое вы применяете к системе, чем самой системой. Вот почему вы должны строить свои системы (или торговые методы, если вы настроены против механических систем), будучи уверенными в том, что они останутся прибыльными (даже если только минимально прибыльными) в будущем. Помните, что этого нельзя достичь путем ограничения степеней свободы системы или метода. При разработке вашей системы или метода помните также о фундаментальном уравнении торговли. Оно будет вести вас в верном направлении в отношении эффективности системы или метода. Когда оно будет использоваться вместе с принципом «неограничения степеней свободы», вы получите метод или систему и сможете применить различные техники управления деньгами. Использование этих методов управления деньгами, будь они эмпирическими, которые описываются в этой главе, или параметрическими (ими мы займемся в главе 3), определит степень прибыльности вашего метода или системы.
Мы можем получить гораздо больше, чем просто понимание того факта, что уменьшение размера проигрышей улучшает конечный результат. Вернемся к уравнению (1.19а):
Подставим А вместо AHPR (среднее арифметическое HPR). Далее, так как (X ^Y) ^ Z = Х ^ (Y * Z), мы можем еще больше упростить уравнение:
Это последнее уравнение мы назовем фундаментальным уравнением торговли, так как оно описывает, как различные факторы: А, SD и N — влияют на результат торговли. Очевидны несколько фактов. Во-первых, если А меньше или равно единице, тогда при любых значениях двух других переменных, SD и N, наш результат не может быть больше единицы. Если А меньше единицы, то при N, стремящемся к бесконечности, наш результат приближается к нулю. Это означает, что, если А меньше или равно 1 (математическое ожидание меньше или равно нулю, так как математическое ожидание равно А - 1), у нас нет шансов получить прибыль. Фактически, если А меньше 1, то наше разорение — это просто вопрос времени (то есть достаточно большого N).
При условии, что А больше 1, сростом N увеличивается наша прибыль. Например, система показала среднее арифметическое 1,1 и стандартное отклонение 0,25. Таким образом:
В нашем примере, где коэффициент равен 1,1475; 1,1475 ^ (1/2) = 1,071214264. Таким образом, каждая следующая сделка, каждое увеличение N на единицу

соответствует умножению нашего конечного счета на 1,071214264. Отметьте, что это число является средним геометрическим. Каждый раз, когда осуществляется сделка и когда N увеличивается на единицу, коэффициент умножается на среднее геометрическое. В этом и состоит действительная польза диверсификации, выраженная математически фундаментальным уравнением торговли. Диверсификация позволяет вам как бы увеличить N (т.е. количество сделок) за определенный период времени. Есть еще одна важная деталь, которую необходимо отметить при рассмотрении фундаментального уравнения торговли: хорошо, когда вы уменьшаете стандартное отклонение больше, чем арифметическое среднее HPR. Поэтому следует быстро закрывать убыточные позиции (использовать маленький stop-loss). Но уравнение также демонстрирует, что при выборе слишком жесткого стопа вы можете больше потерять. Вас выбьет с рынка из-за слишком большого количества сделок с маленьким проигрышем, которые позднее оказались бы прибыльными, поскольку А уменьшается в большей степени, чем SD. Вместе с тем, и уменьшение больших выигрышных сделок поможет вашей системе, если это уменьшает SD больше, чем уменьшает А. Во многих случаях этого можно достичь путем включения в вашу торговую программу опционов. Позиция по опционам, которая направлена против позиции базового инструмента (покупка опциона или продажа соответствующего опциона), может оказаться весьма полезной. Например, если у вас длинная позиция по какой-либо акции (или товару), покупка пут-опциона (или продажа колл-опциона) может уменьшить ваше SD по совокупной позиции в большей степени, чем уменьшить А. Если вы получаете прибыль по базовому инструменту, то будете в убытке по опциону. При этом убыток опциону лишь незначительно уменьшит общую прибыль. Таким образом, вы уменьшили как ваше SD, так и А. Если вы не получаете прибыль по базовому инструменту, вам надо увеличить А и уменьшить SD. Надо стремиться уменьшить SD в большей степени, чем уменьшить А.
Конечно, издержки на трансакции при такой стратегии довольно значительны, и они всегда должны приниматься в расчет. Чтобы воспользоваться такой стратегией, ваша программа не должна быть ориентирована на очень короткий срок. Все вышесказанное лишь подтверждает, что различные стратегии и различные торговые правила должны рассматриваться сточки зрения фундаментального уравнения торговли. Таким образом, мы можем оценить влияние этих факторов на уровень возможных убытков и понять, что именно необходимо сделать для улучшения системы.
Допустим, в долгосрочной торговой программе была использована выше- упомянутая стратегия покупки пут-опциона совместно с длинной позицией по базовому инструменту, в результате мы получили большее оценочное TWR. Ситуация, когда одновременно открыты длинная позиция по базовому инструменту и позиция по пут-опциону, эквивалентна просто длинной позиции по колл-опциону. В том случае лучше просто купить колл-опцион, так как издержки на трансакции будут существенно ниже1, чем при наличии длинной позиции по базовому инструменту и длинной позиции по пут-опциону. Продемонстрируем это на примере рынка индексов акций в 1987 году. Допустим, мы покупаем базовый инструмент — индекс ОЕХ. Система, которую мы будем использовать, является простым 20-дневным прорывом канала. Каждый день мы рассчитываем самый высокий максимум и самый низкий минимум последних 20 дней. Затем, в течение дня, если рынок повышается и касается верхней точки, мы покупаем. Если цены идут вниз и касаются низшей точки, мы продаем. Если дневные открытия выше или ниже точек входа в рынок, мы входим при открытии. Такая система подразумевает постоянную торговлю на рынке:
1 Здесь есть еще один плюс, который сразу может быть и не виден. Он состоит в том, что мы заранее знаем проигрыш худшего случая. Учитывая, насколько чувствительно уравнение оптимального f к наибольшему проигрышу, такая стратегия может приблизить нас к пику кривой f и показать, каким может быть наибольший проигрыш. Во-вторых, проблема проигрыша в 3 стандартных отклонениях (или больше) с более высокой вероятностью, чем подразумевает нормальное распределение, будет устранена. Именно гигантские проигрыши более 3 стандартных отклонений разоряют большинство трейдеров. Опционные стратегии могут полностью упразднить такие проигрыши.
Если определять оптимальное
ветствующее среднее геометрическое (фактор роста на нашем счете за игру) равно 1,12445.
Теперь мы возьмем те же сделки, только будем использовать модель оценки фондовых опционов Блэка-Шоулса (подробно об этом будет рассказано в главе 5), и преобразуем входные цены в теоретические цены опционов. Входные данные для ценовой модели будут следующими: историческая волатильность, рассчитанная на основе 20 дней (расчет исторической волатильности также приводится в главе 5), безрисковая ставка 6% и 260,8875 дней (это среднее число рабочих дней в году). Далее мы допустим, что покупаем опционы, когда остается ровно 0,5 года до даты их исполнения (6 месяцев), и что они «при деньгах». Другими словами, существуют цены исполнения, в точности соответствующие цене входа на рынок. Покупка коллопциона, когда система в длинной позиции по базовому инструменту, и пут-опциона, когда система в короткой позиции по базовому инструменту, с учетом параметров упомянутой модели оценки опционов, даст в результате следующий поток сделок:
Если рассчитать оптимальное f по этому потоку сделок, мы придем к выводу, что соответствующее среднее геометрическое (фактор роста на нашем счете за игру) равно 1,2166. Сравните его со средним геометрическим при оптимальном f для базового инструмента 1,12445. Разница огромная. Так как мы получили всего б сделок, то можно возвести каждое среднее геометрическое в 6-ую степень для определения TWR. Это даст TWR по базовому инструменту 2,02 против TWR по опционам 3,24. Преобразуем TWR в процент прибыли от нашего начального счета. Мы получим 102% прибыли при торговле по базовому инструменту и 224% прибыли при торговле опционами. Опционы в рассмотренном случае предпочтительнее, что подтверждается фундаментальным уравнением торговли.
Длинные позиции по опционам могут быть менее эффективными, чем длинные позиции по базовому инструменту. Чтобы не сделать здесь ошибку, торговые стратегии (а также выбор серии опционов) необходимо рассматривать с точки зрения фундаментального уравнения торговли.
Как видите, фундаментальное уравнение торговли можно использовать для улучшения торговли. Улучшения могут заключаться в изменении жесткости при- казов на закрытие убыточных позиций (stop-loss приказов), в установлении целей и так далее. Эти изменения могут быть вызваны неэффективностью текущей тор- говли, а также неэффективностью торговой методологии.
Надеюсь, вы теперь понимаете, что компьютер неверно используется большин- ством трейдеров. Оптимизация, поиск систем и значений параметров, которые бы заработали больше всего денег на прошлых данных,— по сути пустая трата времени. Вам надо получить систему, которая будет прибыльна в будущем. С помощью грамотного управления капиталом вы сможете «выжать» максимум из системы, которая лишь минимально прибыльна. Прибыльность системы в большей степени определяется управлением капиталом, которое вы применяете к системе, чем самой системой. Вот почему вы должны строить свои системы (или торговые методы, если вы настроены против механических систем), будучи уверенными в том, что они останутся прибыльными (даже если только минимально прибыльными) в будущем. Помните, что этого нельзя достичь путем ограничения степеней свободы системы или метода. При разработке вашей системы или метода помните также о фундаментальном уравнении торговли. Оно будет вести вас в верном направлении в отношении эффективности системы или метода. Когда оно будет использоваться вместе с принципом «неограничения степеней свободы», вы получите метод или систему и сможете применить различные техники управления деньгами. Использование этих методов управления деньгами, будь они эмпирическими, которые описываются в этой главе, или параметрическими (ими мы займемся в главе 3), определит степень прибыльности вашего метода или системы.
Вложения
FXWizard
Гуру форума
Глава 2
Характеристики торговли фиксированной долей и полезные методы
Мы видели, что оптимальный рост счета достигается посредством оптимального f. Это верно независимо от инструмента, используемого в торговле. Работаем ли мы на рынке фьючерсов, акций или опционов, управляем ли группой трейдеров, при оптимальном f достигается оптимальный рост, а поставленная цель — в кратчайшее время. Мы также узнали, как с эмпирической точки зрения объединить различные рыночные системы на их оптимальных уровнях f в оптимальный портфель, то есть как скомбинировать оптимальное f и теорию портфеля, используя прошлые данные для определения весов компонентов в оптимальном портфеле. Далее мы рассмотрим важные характеристики торговли фиксированной долей.
Оптимальное F для начинающих трейдеров с небольшими капиталами
Каким образом при небольшом счете, который дает возможность торговать только 1 контрактом, использовать подход оптимального f? Одно из предложений заключается в том, чтобы торговать 1 контрактом, учитывая не только оптималь- ное IB долларах (наибольший проигрыш / -f), но также проигрыш и маржу (залог). Сумма средств, отведенная под первый контракт, должна быть больше суммы оптимального IB долларах или маржи плюс максимальный исторический проигрыш (на основе 1 единицы):
где А =сумма в долларах, отведенная под первый контракт;
f =оптимальное f (от 0 до 1);
Маржа =первоначальная спекулятивная маржа для данного контрак та средства, необходимые для открытия одного контракта);
Проигрыш =максимальный исторический совокупный проигрыш; МАХ {} = максимальное значение выражения в скобках;
ABS() = функция абсолютного значения.
(залоговые
При такой процедуре вы сможете пережить максимальный проигрыш и все еще иметь достаточно денег для следующей попытки. Хотя мы не можем быть уверены, что в будущем проигрыш наихудшего случая не превысит исторический проигрыш наихудшего случая, маловероятно, чтобы мы начали торговлю сразу с нового исторического проигрыша. Трейдер, использующий эту технику, каждый день должен вычитать сумму, полученную с помощью уравнения (2.01), из своего баланса. Остаток следует разделить на величину (наибольший проигрыш / -f). Полученный ответ следует округлить в меньшую сторону и прибавить единицу, таким образом, мы получим число контрактов для торговли.
Прояснить ситуацию поможет пример. Допустим, у нас есть система, где оптимальное f= 0,4, наибольший исторический проигрыш равен -3000 долларов, максимальный совокупный проигрыш был -6000 долларов, а залог равен 2500 долларов. Используя уравнение (2.01), мы получим:
А = МАХ {(-$3000 / 0,4), ($2500 + ABS(-$6000))} = MAX {($7500), ($2500 + $6000)}
= МАХ {$7500, $8500} == $8500
Таким образом, нам следует отвести 8500 долларов под первый контракт. Теперь допустим, что на нашем счете 22 500 долларов. Поэтому мы вычтем сумму под первый контракт из баланса: $22 500 - $8500 = $14 000 Затем разделим эту сумму на оптимальное f в долларах: $14 000/$7500 =1,867 Округлим полученный результат в меньшую сторону до ближайшего целого числа: INT (1,867)=1 Затем добавим 1 к полученному результату (1 контракт уже обеспечен 8500 долларами,
которые мы вычли из баланса):1+1=2 Таким образом, мы будем торговать 2 контрактами. Если бы мы торговали на уровне оптимального f ($7500 на 1 контракт), то торговали бы 3 контрактами (22 500 / 7500). Как видите, этот метод можно использовать независимо от того, насколько велик баланс счета (однако чем больше баланс, тем ближе будут результаты). Более того, чем больше баланс, тем менее вероятно, что вы в конце концов получите проигрыш, после которого сможете торговать только 1 контрактом. Трейдерам с небольшими счетами или тем, кто только начинает торговать, следует использовать этот подход.
Характеристики торговли фиксированной долей и полезные методы
Мы видели, что оптимальный рост счета достигается посредством оптимального f. Это верно независимо от инструмента, используемого в торговле. Работаем ли мы на рынке фьючерсов, акций или опционов, управляем ли группой трейдеров, при оптимальном f достигается оптимальный рост, а поставленная цель — в кратчайшее время. Мы также узнали, как с эмпирической точки зрения объединить различные рыночные системы на их оптимальных уровнях f в оптимальный портфель, то есть как скомбинировать оптимальное f и теорию портфеля, используя прошлые данные для определения весов компонентов в оптимальном портфеле. Далее мы рассмотрим важные характеристики торговли фиксированной долей.
Оптимальное F для начинающих трейдеров с небольшими капиталами
Каким образом при небольшом счете, который дает возможность торговать только 1 контрактом, использовать подход оптимального f? Одно из предложений заключается в том, чтобы торговать 1 контрактом, учитывая не только оптималь- ное IB долларах (наибольший проигрыш / -f), но также проигрыш и маржу (залог). Сумма средств, отведенная под первый контракт, должна быть больше суммы оптимального IB долларах или маржи плюс максимальный исторический проигрыш (на основе 1 единицы):
где А =сумма в долларах, отведенная под первый контракт;
f =оптимальное f (от 0 до 1);
Маржа =первоначальная спекулятивная маржа для данного контрак та средства, необходимые для открытия одного контракта);
Проигрыш =максимальный исторический совокупный проигрыш; МАХ {} = максимальное значение выражения в скобках;
ABS() = функция абсолютного значения.
(залоговые
При такой процедуре вы сможете пережить максимальный проигрыш и все еще иметь достаточно денег для следующей попытки. Хотя мы не можем быть уверены, что в будущем проигрыш наихудшего случая не превысит исторический проигрыш наихудшего случая, маловероятно, чтобы мы начали торговлю сразу с нового исторического проигрыша. Трейдер, использующий эту технику, каждый день должен вычитать сумму, полученную с помощью уравнения (2.01), из своего баланса. Остаток следует разделить на величину (наибольший проигрыш / -f). Полученный ответ следует округлить в меньшую сторону и прибавить единицу, таким образом, мы получим число контрактов для торговли.
Прояснить ситуацию поможет пример. Допустим, у нас есть система, где оптимальное f= 0,4, наибольший исторический проигрыш равен -3000 долларов, максимальный совокупный проигрыш был -6000 долларов, а залог равен 2500 долларов. Используя уравнение (2.01), мы получим:
А = МАХ {(-$3000 / 0,4), ($2500 + ABS(-$6000))} = MAX {($7500), ($2500 + $6000)}
= МАХ {$7500, $8500} == $8500
Таким образом, нам следует отвести 8500 долларов под первый контракт. Теперь допустим, что на нашем счете 22 500 долларов. Поэтому мы вычтем сумму под первый контракт из баланса: $22 500 - $8500 = $14 000 Затем разделим эту сумму на оптимальное f в долларах: $14 000/$7500 =1,867 Округлим полученный результат в меньшую сторону до ближайшего целого числа: INT (1,867)=1 Затем добавим 1 к полученному результату (1 контракт уже обеспечен 8500 долларами,
которые мы вычли из баланса):1+1=2 Таким образом, мы будем торговать 2 контрактами. Если бы мы торговали на уровне оптимального f ($7500 на 1 контракт), то торговали бы 3 контрактами (22 500 / 7500). Как видите, этот метод можно использовать независимо от того, насколько велик баланс счета (однако чем больше баланс, тем ближе будут результаты). Более того, чем больше баланс, тем менее вероятно, что вы в конце концов получите проигрыш, после которого сможете торговать только 1 контрактом. Трейдерам с небольшими счетами или тем, кто только начинает торговать, следует использовать этот подход.
FXWizard
Гуру форума
Порог геометрической торговли
Существует еще один хороший подход для трейдеров, которые только начинают торговать, правда, если вы не используете только что упомянутый метод. При таком подходе используется еще один побочный продукт оптимального f — порог геометрической торговли. Мы уже знаем такие побочные продукты оптимального f, как TWR, среднее геометрическое и т.д.; они были получены из оптимального f и дают нам информацию о системе. Порог геометрической торговли — это еще один из таких побочных расчетов. По существу, порог геометрической торговли говорит нам, в какой точке следует переключиться на торговлю фиксированной долей, предполагая, что мы начинаем торговать фиксированным количеством контрактов. Вспомните пример с броском монеты, где мы выигрываем 2 доллара, если монета падает на лицевую сторону, и проигрываем 1 доллар, если она падает на обратную сторону. Мы знаем, что оптимальное f= 0,25, т.е. 1 ставка на каждые 4 доллара баланса счета. Если мы торгуем на основе постоянного количества контрактов, то в среднем выигрываем 0,50 долларов за игру. Однако если мы начнем торговать фиксированной долей счета, то можем ожидать выигрыша в 0,2428 доллара на единицу за одну игру (при геометрической средней торговле). Допустим, мы начинаем с первоначального счета в 4 доллара и поэтому делаем 1 ставку за одну игру. В конце концов, когда счет увеличивается до 8 долларов, сле- дует делать 2 ставки за одну игру. Однако 2 ставки, умноженные на геометрическую среднюю торговлю 0,2428 доллара, дадут в итоге 0,4856 доллара. Не лучше ли придерживаться 1 ставки при уровне баланса 8 долларов, так как нашим ожиданием за одну игру все еще будет 0,50 доллара? Ответ — «да». Причина в том, что оптимальное f рассчитывается на основе контрактов, которые бесконечно делимы, чего в реальной торговле не бывает.
Мы можем найти точку, где следует перейти к торговле двумя контрактами, основываясь на формуле порога геометрической торговли Т:
Т = ААТ / GAT * Наибольший убыток / -f, где Т = порог геометрической торговли; ААТ = средняя арифметическая сделка; GAT = средняя геометрическая сделка;
f= оптимальное f (от 0 до 1). Для нашего примера с броском монеты (2 к I): Т=0,50 / 0,2428*-1 / -0,25 =8,24
Поэтому следует переходить на торговлю двумя контрактами, когда счет увеличится до 8,24 доллара, а не до 8,00 долларов. Рисунок 2-1 иллюстрирует порог гео- метрической торговли для игры с 50% шансов выигрыша 2 долларов и 50% шансов проигрыша 1 доллара. Отметьте, что дно кривой порога геометрической торговли соответствует оптимальному f. Порог геометрической торговли является оптимальным уровнем баланса для перехода от торговли одной единицей к торговле двумя единицами. Поэтому если вы используете оптимальное f, то сможете перейти к геометрической торговле при минимальном уровне баланса счета. Теперь возникает вопрос: «Можем ли мы использовать подобный подход, чтобы узнать, когда переходить от 2 к 3 контрактам?», а также: «Почему в самом начале размер единицы не может быть 100 контрактов, если вы начинаете с достаточно большого счета, а не такого, который позволяет торговать лишь одним контрактом?» Разумеется, можно использовать этот метод при работе с размером единицы, большим 1. Однако это корректно в том случае, если вы не уменьшите размер единицы до перехода к геометрическому способу торговли. Дело в том, что до того, как вы перейдете на геометрическую торговлю, вы должны будете торговать постоянным размером единицы.
Допустим, вы начинаете со счета в 400 единиц в игре с броском монеты 2 к 1. Оптимальное f в долларах предполагает торговлю 1 контрактом (1 ставка) на каждые 4 доллара на счете. Поэтому начинайте торговать 100 контрактами (сделав 100 ставок) в первой сделке. Ваш порог геометрической торговли равен 8,24 доллара, и поэтому следует торговать 101 контрактом на уровне баланса 404,24 доллара. Вы можете преобразовать порог геометрической торговли, который соответствует переходу с 1 контракта к 2 следующим образом:

Рисунок 2-1 Порог геометрической торговли для броска монеты 2 к 1
Преобразованное Т = EQ + Т - (Наибольший проигрыш / -f),
где EQ = начальный уровень баланса счета;
Т = порог геометрической торговли для перехода с одного контракта к двум;
f= оптимальное f (от 0 до 1).
Преобразованное Т = 400 + 8,24 - (-1 / -0,25) = 400 + 8,24 - 4 = 404,24
Таким образом, вы перейдете к торговле 101 контрактом (101 ставке), только когда баланс счета достигнет 404,24 доллара. Допустим, вы торгуете постоянным количеством контрактов, пока баланс счета не достигнет 404,24 доллара, где вы начнете применять геометрический подход. Пока баланс счета не достигнет 404,24 доллара, вы будете торговать 100 контрактами в последующих сделках независимо от суммы счета. Если после того, как вы пересечете порог геометрической торговли (то есть после того, как баланс счета достигнет 404,24 доллара), вы понесете убыток и баланс упадет ниже 404,24 доллара, вы вернетесь снова к торговле на основе 100 контрактов и будете так торговать до тех пор, пока снова не пересечете геометрический порог. Невозможность уменьшения количества контрактов при уменьшении счета, когда вы находитесь ниже геометрического порога, является недостатком при использовании этой процедуры, когда контрактов больше 2. Если вы торгуете только 1 контрактом, геометрический порог является реальным методом для определения того, на каком уровне баланса начать торговать 2 контрактами (так как вы не можете торговать менее чем 1 контрактом при понижении баланса). Однако этот метод не работает, когда речь идет о переходе от 2 контрактов к 3, так как метод базируется на том, что вы начинаете торговлю с постоянного количества контрактов. То есть, если вы торгуете 2 контрактами, метод не будет работать (за исключением случая, когда вы откажетесь от возможности понизить количество контрактов до одного при падении уровня баланса). Таким образом, начиная торговлю со 100 контрактов, вы не можете перейти к торговле меньшим числом контрактов. Если вы не будете уменьшать количество контрактов, которыми в настоящее время торгуете, при понижении баланса, то порог геометрической торговли или его преобразованная версия из уравнения (2.03) будет уровнем баланса, достаточным для добавления следующего контракта. Проблема этой операции (не уменьшать при понижении) состоит в том, что вы заработаете меньше (TWR будет меньше) в асимптотическом смысле. Вы не выиграете столько, сколько бы выиграли при торговле полным оптимальным f. Более того, ваши проигрыши будут больше, и риск банкротства увеличится. Поэтому порог геометрической торговли будет эффективен, если вы начнете с наименьшего размера ставки (1 контракт) и повысите его до 2. Оптимально, если средняя арифметическая сделка более чем в два раза превышает среднюю геометрическую сделку. Предложенный метод следует использовать, когда вы не можете торговать дробными единицами.
Существует еще один хороший подход для трейдеров, которые только начинают торговать, правда, если вы не используете только что упомянутый метод. При таком подходе используется еще один побочный продукт оптимального f — порог геометрической торговли. Мы уже знаем такие побочные продукты оптимального f, как TWR, среднее геометрическое и т.д.; они были получены из оптимального f и дают нам информацию о системе. Порог геометрической торговли — это еще один из таких побочных расчетов. По существу, порог геометрической торговли говорит нам, в какой точке следует переключиться на торговлю фиксированной долей, предполагая, что мы начинаем торговать фиксированным количеством контрактов. Вспомните пример с броском монеты, где мы выигрываем 2 доллара, если монета падает на лицевую сторону, и проигрываем 1 доллар, если она падает на обратную сторону. Мы знаем, что оптимальное f= 0,25, т.е. 1 ставка на каждые 4 доллара баланса счета. Если мы торгуем на основе постоянного количества контрактов, то в среднем выигрываем 0,50 долларов за игру. Однако если мы начнем торговать фиксированной долей счета, то можем ожидать выигрыша в 0,2428 доллара на единицу за одну игру (при геометрической средней торговле). Допустим, мы начинаем с первоначального счета в 4 доллара и поэтому делаем 1 ставку за одну игру. В конце концов, когда счет увеличивается до 8 долларов, сле- дует делать 2 ставки за одну игру. Однако 2 ставки, умноженные на геометрическую среднюю торговлю 0,2428 доллара, дадут в итоге 0,4856 доллара. Не лучше ли придерживаться 1 ставки при уровне баланса 8 долларов, так как нашим ожиданием за одну игру все еще будет 0,50 доллара? Ответ — «да». Причина в том, что оптимальное f рассчитывается на основе контрактов, которые бесконечно делимы, чего в реальной торговле не бывает.
Мы можем найти точку, где следует перейти к торговле двумя контрактами, основываясь на формуле порога геометрической торговли Т:
Т = ААТ / GAT * Наибольший убыток / -f, где Т = порог геометрической торговли; ААТ = средняя арифметическая сделка; GAT = средняя геометрическая сделка;
f= оптимальное f (от 0 до 1). Для нашего примера с броском монеты (2 к I): Т=0,50 / 0,2428*-1 / -0,25 =8,24
Поэтому следует переходить на торговлю двумя контрактами, когда счет увеличится до 8,24 доллара, а не до 8,00 долларов. Рисунок 2-1 иллюстрирует порог гео- метрической торговли для игры с 50% шансов выигрыша 2 долларов и 50% шансов проигрыша 1 доллара. Отметьте, что дно кривой порога геометрической торговли соответствует оптимальному f. Порог геометрической торговли является оптимальным уровнем баланса для перехода от торговли одной единицей к торговле двумя единицами. Поэтому если вы используете оптимальное f, то сможете перейти к геометрической торговле при минимальном уровне баланса счета. Теперь возникает вопрос: «Можем ли мы использовать подобный подход, чтобы узнать, когда переходить от 2 к 3 контрактам?», а также: «Почему в самом начале размер единицы не может быть 100 контрактов, если вы начинаете с достаточно большого счета, а не такого, который позволяет торговать лишь одним контрактом?» Разумеется, можно использовать этот метод при работе с размером единицы, большим 1. Однако это корректно в том случае, если вы не уменьшите размер единицы до перехода к геометрическому способу торговли. Дело в том, что до того, как вы перейдете на геометрическую торговлю, вы должны будете торговать постоянным размером единицы.
Допустим, вы начинаете со счета в 400 единиц в игре с броском монеты 2 к 1. Оптимальное f в долларах предполагает торговлю 1 контрактом (1 ставка) на каждые 4 доллара на счете. Поэтому начинайте торговать 100 контрактами (сделав 100 ставок) в первой сделке. Ваш порог геометрической торговли равен 8,24 доллара, и поэтому следует торговать 101 контрактом на уровне баланса 404,24 доллара. Вы можете преобразовать порог геометрической торговли, который соответствует переходу с 1 контракта к 2 следующим образом:
Рисунок 2-1 Порог геометрической торговли для броска монеты 2 к 1
Преобразованное Т = EQ + Т - (Наибольший проигрыш / -f),
где EQ = начальный уровень баланса счета;
Т = порог геометрической торговли для перехода с одного контракта к двум;
f= оптимальное f (от 0 до 1).
Преобразованное Т = 400 + 8,24 - (-1 / -0,25) = 400 + 8,24 - 4 = 404,24
Таким образом, вы перейдете к торговле 101 контрактом (101 ставке), только когда баланс счета достигнет 404,24 доллара. Допустим, вы торгуете постоянным количеством контрактов, пока баланс счета не достигнет 404,24 доллара, где вы начнете применять геометрический подход. Пока баланс счета не достигнет 404,24 доллара, вы будете торговать 100 контрактами в последующих сделках независимо от суммы счета. Если после того, как вы пересечете порог геометрической торговли (то есть после того, как баланс счета достигнет 404,24 доллара), вы понесете убыток и баланс упадет ниже 404,24 доллара, вы вернетесь снова к торговле на основе 100 контрактов и будете так торговать до тех пор, пока снова не пересечете геометрический порог. Невозможность уменьшения количества контрактов при уменьшении счета, когда вы находитесь ниже геометрического порога, является недостатком при использовании этой процедуры, когда контрактов больше 2. Если вы торгуете только 1 контрактом, геометрический порог является реальным методом для определения того, на каком уровне баланса начать торговать 2 контрактами (так как вы не можете торговать менее чем 1 контрактом при понижении баланса). Однако этот метод не работает, когда речь идет о переходе от 2 контрактов к 3, так как метод базируется на том, что вы начинаете торговлю с постоянного количества контрактов. То есть, если вы торгуете 2 контрактами, метод не будет работать (за исключением случая, когда вы откажетесь от возможности понизить количество контрактов до одного при падении уровня баланса). Таким образом, начиная торговлю со 100 контрактов, вы не можете перейти к торговле меньшим числом контрактов. Если вы не будете уменьшать количество контрактов, которыми в настоящее время торгуете, при понижении баланса, то порог геометрической торговли или его преобразованная версия из уравнения (2.03) будет уровнем баланса, достаточным для добавления следующего контракта. Проблема этой операции (не уменьшать при понижении) состоит в том, что вы заработаете меньше (TWR будет меньше) в асимптотическом смысле. Вы не выиграете столько, сколько бы выиграли при торговле полным оптимальным f. Более того, ваши проигрыши будут больше, и риск банкротства увеличится. Поэтому порог геометрической торговли будет эффективен, если вы начнете с наименьшего размера ставки (1 контракт) и повысите его до 2. Оптимально, если средняя арифметическая сделка более чем в два раза превышает среднюю геометрическую сделку. Предложенный метод следует использовать, когда вы не можете торговать дробными единицами.
Вложения
FXWizard
Гуру форума
Один комбинированный денежный счет по сравнению с отдельными денежными счетами
Прежде чем мы обсудим параметрические методы, необходимо рассмотреть не- которые очень важные вопросы в отношении торговли фиксированной долей. Во- первых, при одновременной торговле более чем в одной рыночной системе вы получите лучшие результаты в асимптотическом смысле, если будете использовать только один комбинированный денежный счет. Рассчитывать количество контрактов для торговли следует не для каждого отдельно взятого денежного счета, а для этого единого комбинированного счета.
По этой причине необходимо ежедневно «соединять» подсчета при изменении их балансов. Сравним две похожие системы: систему А и систему Б. Обе системы имеют 50% шанс выигрыша и обе имеют отношение выигрыша 2:1. Поэтому оптимальное f диктует, чтобы мы ставили 1 доллар на каждые 4 доллара баланса. Первый пример описывает ситуацию, когда эти две системы имеют положитель- ную корреляцию. Мы начинаем со 100 долларов и разбиваем их на 2 подсчета по 50 долларов каждый. После регистрации сделки для этой системы изменится только столбец «Полный капитал», так как каждая система имеет свой собствен- ный отдельный счет. Размер денежного счета каждой системы используется для определения ставки для последующей игры:

Теперь мы рассмотрим комбинированный счет в 100 единиц. Вместо того чтобы ставить 1 доллар на каждые 4 доллара на комбинированном счете для каждой сис- темы, мы будем ставить 1 доллар на каждые 8 долларов комбинированного счета. Каждая сделка для любой системы затрагивает комбинированный счет, и именно комбинированный счет используется для определения размера ставки для после- дующей игры (Таблица II).
Отметьте, что в случае комбинированного счета и в случае отдельных счетов прибыль одна и та же: $42,38. Мы рассматривали положительную корреляцию между двумя системами. Теперь рассмотрим случай с отрицательной корреляцией между теми же системами, для двух отдельных денежных счетов (Таблица III):


Как видите, при работе с отдельными денежными счетами обе системы выигрывают ту же сумму независимо от корреляции. Однако при комбинированном счете:

При использовании комбинированного счета результаты гораздо лучше. Таким образом, торговать фиксированной долей следует на основе одного комбинированного счета.
Прежде чем мы обсудим параметрические методы, необходимо рассмотреть не- которые очень важные вопросы в отношении торговли фиксированной долей. Во- первых, при одновременной торговле более чем в одной рыночной системе вы получите лучшие результаты в асимптотическом смысле, если будете использовать только один комбинированный денежный счет. Рассчитывать количество контрактов для торговли следует не для каждого отдельно взятого денежного счета, а для этого единого комбинированного счета.
По этой причине необходимо ежедневно «соединять» подсчета при изменении их балансов. Сравним две похожие системы: систему А и систему Б. Обе системы имеют 50% шанс выигрыша и обе имеют отношение выигрыша 2:1. Поэтому оптимальное f диктует, чтобы мы ставили 1 доллар на каждые 4 доллара баланса. Первый пример описывает ситуацию, когда эти две системы имеют положитель- ную корреляцию. Мы начинаем со 100 долларов и разбиваем их на 2 подсчета по 50 долларов каждый. После регистрации сделки для этой системы изменится только столбец «Полный капитал», так как каждая система имеет свой собствен- ный отдельный счет. Размер денежного счета каждой системы используется для определения ставки для последующей игры:
Теперь мы рассмотрим комбинированный счет в 100 единиц. Вместо того чтобы ставить 1 доллар на каждые 4 доллара на комбинированном счете для каждой сис- темы, мы будем ставить 1 доллар на каждые 8 долларов комбинированного счета. Каждая сделка для любой системы затрагивает комбинированный счет, и именно комбинированный счет используется для определения размера ставки для после- дующей игры (Таблица II).
Отметьте, что в случае комбинированного счета и в случае отдельных счетов прибыль одна и та же: $42,38. Мы рассматривали положительную корреляцию между двумя системами. Теперь рассмотрим случай с отрицательной корреляцией между теми же системами, для двух отдельных денежных счетов (Таблица III):
Как видите, при работе с отдельными денежными счетами обе системы выигрывают ту же сумму независимо от корреляции. Однако при комбинированном счете:
При использовании комбинированного счета результаты гораздо лучше. Таким образом, торговать фиксированной долей следует на основе одного комбинированного счета.
Вложения
FXWizard
Гуру форума
Рассматривайте каждую игру как бесконечно повторяющуюся
Следующая аксиома, касающаяся торговли фиксированной долей, относится к максимизации текущего события, как будто оно должно быть осуществлено бес- конечное количество раз в будущем. Мы определили, что для процесса независи- мых испытаний вы должны всегда использовать оптимальное и постоянное f, но при наличии зависимости оптимальное f уже не будет постоянной величиной.
Допустим, в нашей системе существует зависимость, в соответствии с которой подобное порождает подобное, а доверительная граница достаточно высока. Для наглядности мы будем использовать уже знакомую нам игру 2:1. Система показывает, что если последняя игра выигрышная, то следующая игра имеет 55% шанс выигрыша. Если последняя игра проигрышная, то следующая игра имеет 45% шанс проигрыша. Таким образом, если последняя игра была выигрышная, то исходя из формулы Келли, уравнение (1.10) для поиска оптимального f (так как результаты игры имеют бернуллиево распределение), получим:
(1.10) f =((2+1)* 0,55-1)/2 =(3*0,55- 1)/2=0,65/2=0,325 После проигрышной игры наше оптимальное f равно:
f =((2+1)* 0,45-1)/2 =(3*0,45-1) /2 =0,35/2 =0,175
Разделив наибольший проигрыш системы (т.е. -1) на отрицательные оптимальные f, мы получим 1 ставку на каждые 3,076923077 единицы на счете после выигрыша и 1 ставку на каждые 5,714285714 единицы на счете после проигрыша. Таким образом мы максимизируем рост в долгосрочной перспективе.
Отметьте, что в этом примере ставки как после выигрышей, так и после проигрышей все еще имеют положительное математическое ожидание. Что произойдет, если после проигрыша вероятность выигрыша будет равна 0,3? В таком случае математическое ожидание имеет отрицательное значение и оп- тимального f не существует, таким образом, вам не следует использовать эту игру: (1.03) М0=(0,3*2)+(0,7*-1) =0,6-0,7 =-0,1
В этом случае следует использовать оптимальное количество только после выиг- рыша и не торговать после проигрыша. Если зависимость действительно суще- ствует, вы должны изолировать сделки рыночной системы, основанные на зави- симости, и обращаться с изолированными сделками как с отдельными рыночными системами. Принцип, состоящий в том, что асимптотический рост максимизируется, когда каждая игра осуществляется бесконечное количество раз в будущем, также применим к нескольким одновременным играм (или торговле портфелем).
Рассмотрим две системы ставок, А и Б. Обе имеют отношение выигрыша к проигрышу 2:1, и обе выигрывают 50% времени. Допустим, что коэффициент корреляции между двумя системами равен 0. Оптимальные f для обеих систем (при раздельной, а не одновременной торговле) составляют 0,25 (т.е. одна ставка на каждые 4 единицы на балансе). Оптимальные f при одновременной торговле в обеих системах составляют 0,23 (т.е. 1 ставка на каждые 4,347826087 единицы на балансе счета). В случае, когда система Б торгует только две трети времени, неко- торые трейдеры разорятся, если обе системы не будут торговать одновременно. Первая последовательность показана при начальном комбинированном счете в 1000 единиц, и для каждой системы оптимальное f соответствует 1 ставке на каж- дые 4,347826087 единицы:

Рассмотрим теперь ситуацию, когда А торгует отдельно от Б. В этом случае мы де- лаем 1 ставку на каждые 4 единицы на комбинированном счете для системы А (так как это оптимальное f для одной игры). В игре с одновременными ставками мы все равно ставим 1 единицу на каждые 4,347826087 единицы на балансе счета как для А, так и для Б. Отметьте, что независимо от того, отдельная это ставка или одновременная ставка по А и Б, мы применяем то оптимальное f, которое увеличивает доход при бесконечном повторении ставок.

Как видите, с помощью этого метода мы получаем небольшой выигрыш, и чем больше сделок проходит, тем больше этот выигрыш. Тот же принцип применяется к торговле портфелем, где не все компоненты портфеля находятся на рынке в определенный момент времени. Вам следует торговать на оптимальных уровнях для комбинации компонентов (или одного компонента), чтобы получить в итоге оптимальный рост, как будто этой комбинацией компонентов (или одним компонентом) придется торговать бесконечное количество раз в будущем.
Следующая аксиома, касающаяся торговли фиксированной долей, относится к максимизации текущего события, как будто оно должно быть осуществлено бес- конечное количество раз в будущем. Мы определили, что для процесса независи- мых испытаний вы должны всегда использовать оптимальное и постоянное f, но при наличии зависимости оптимальное f уже не будет постоянной величиной.
Допустим, в нашей системе существует зависимость, в соответствии с которой подобное порождает подобное, а доверительная граница достаточно высока. Для наглядности мы будем использовать уже знакомую нам игру 2:1. Система показывает, что если последняя игра выигрышная, то следующая игра имеет 55% шанс выигрыша. Если последняя игра проигрышная, то следующая игра имеет 45% шанс проигрыша. Таким образом, если последняя игра была выигрышная, то исходя из формулы Келли, уравнение (1.10) для поиска оптимального f (так как результаты игры имеют бернуллиево распределение), получим:
(1.10) f =((2+1)* 0,55-1)/2 =(3*0,55- 1)/2=0,65/2=0,325 После проигрышной игры наше оптимальное f равно:
f =((2+1)* 0,45-1)/2 =(3*0,45-1) /2 =0,35/2 =0,175
Разделив наибольший проигрыш системы (т.е. -1) на отрицательные оптимальные f, мы получим 1 ставку на каждые 3,076923077 единицы на счете после выигрыша и 1 ставку на каждые 5,714285714 единицы на счете после проигрыша. Таким образом мы максимизируем рост в долгосрочной перспективе.
Отметьте, что в этом примере ставки как после выигрышей, так и после проигрышей все еще имеют положительное математическое ожидание. Что произойдет, если после проигрыша вероятность выигрыша будет равна 0,3? В таком случае математическое ожидание имеет отрицательное значение и оп- тимального f не существует, таким образом, вам не следует использовать эту игру: (1.03) М0=(0,3*2)+(0,7*-1) =0,6-0,7 =-0,1
В этом случае следует использовать оптимальное количество только после выиг- рыша и не торговать после проигрыша. Если зависимость действительно суще- ствует, вы должны изолировать сделки рыночной системы, основанные на зави- симости, и обращаться с изолированными сделками как с отдельными рыночными системами. Принцип, состоящий в том, что асимптотический рост максимизируется, когда каждая игра осуществляется бесконечное количество раз в будущем, также применим к нескольким одновременным играм (или торговле портфелем).
Рассмотрим две системы ставок, А и Б. Обе имеют отношение выигрыша к проигрышу 2:1, и обе выигрывают 50% времени. Допустим, что коэффициент корреляции между двумя системами равен 0. Оптимальные f для обеих систем (при раздельной, а не одновременной торговле) составляют 0,25 (т.е. одна ставка на каждые 4 единицы на балансе). Оптимальные f при одновременной торговле в обеих системах составляют 0,23 (т.е. 1 ставка на каждые 4,347826087 единицы на балансе счета). В случае, когда система Б торгует только две трети времени, неко- торые трейдеры разорятся, если обе системы не будут торговать одновременно. Первая последовательность показана при начальном комбинированном счете в 1000 единиц, и для каждой системы оптимальное f соответствует 1 ставке на каж- дые 4,347826087 единицы:
Рассмотрим теперь ситуацию, когда А торгует отдельно от Б. В этом случае мы де- лаем 1 ставку на каждые 4 единицы на комбинированном счете для системы А (так как это оптимальное f для одной игры). В игре с одновременными ставками мы все равно ставим 1 единицу на каждые 4,347826087 единицы на балансе счета как для А, так и для Б. Отметьте, что независимо от того, отдельная это ставка или одновременная ставка по А и Б, мы применяем то оптимальное f, которое увеличивает доход при бесконечном повторении ставок.
Как видите, с помощью этого метода мы получаем небольшой выигрыш, и чем больше сделок проходит, тем больше этот выигрыш. Тот же принцип применяется к торговле портфелем, где не все компоненты портфеля находятся на рынке в определенный момент времени. Вам следует торговать на оптимальных уровнях для комбинации компонентов (или одного компонента), чтобы получить в итоге оптимальный рост, как будто этой комбинацией компонентов (или одним компонентом) придется торговать бесконечное количество раз в будущем.
Вложения
FXWizard
Гуру форума
Потеря эффективности при одновременных ставках или торговле портфелем
Давайте вернемся к нашей игре с броском монеты 2:1. Допустим, мы собираемся одновременно сыграть в две игры: А и Б, — и существует нулевая корреляция между результатами этих двух игр. Оптимальные f для такого случая соответству- ют ставке в 1 единицу на каждые 4,347826 единицы на балансе счета, когда игры проводятся одновременно. Отметьте, что при начальном счете в 100 единиц мы заканчиваем с результатом в 156,86 единицы:

Теперь давайте рассмотрим систему В. Она будет такой же, как система А и Б, только мы будем играть в эту игру без одновременного ведения другой игры. Мы сыграем 8 раз, но не 2 игры по 4 раза, как в прошлом примере. Теперь наше оптимальное f - это ставка 1 единицы на каждые 4 единицы на балансе счета. Мы, как и прежде, имеем те же 8 сделок, но лучший конечный результат (Таблица VI). Мы получили лучший конечный результат не потому, что оптимальные f немного отличаются (оба значения f находятся на соответствующих оптимальных уровнях), а потому, что есть небольшая потеря эффективности при одновременных ставках. Неэффективность является результатом невозможности изменения структуры вашего счета (т.е. рекапитализации) после каждой отдельной ставки, как в игре только по одной рыночной системе. В случае с двумя одновременными
ставками вы можете рекапитализировать счет только 3 раза, в то время как в слу- чае с 8 отдельными ставками вы рекапитализируете счет 7 раз. Отсюда возникает потеря эффективности при одновременных ставках (или при торговле портфелем рыночных систем).

Мы рассмотрели случай, когда одновременные ставки не были коррелирова-ны. Давайте посмотрим, что произойдет при положительной корреляции (+1,00):

Отметьте, что после 4 одновременных игр при корреляции между рыночными системами +1,00 мы увеличили первоначальный счет 100 единиц до 126,56. Это соответствует TWR = 1,2656, или среднему геометрическому (даже если это ком- бинированные игры) 1,2656 ^ (1/4) =1,06066. Теперь вернемся к случаю с одной ставкой. Обратите внимание, что после 4 игр мы получим 126,56 при начальном счете в 100 единиц. Таким образом, среднее геометрическое равно 1,06066. Это говорит о том, что скорость роста такая же, как и при торговле с оптимальными долями на абсолютно коррелированных рынках. Как только коэффициент корреляции опускается ниже +1,00, скорость роста повышается. Таким образом, мы можем утверждать, что при комбинировании рыночных систем ваша скорость роста никогда не будет меньше, чем в случае одиночной ставки по каждой системе, независимо от того, насколько высоки корреляции, при условии,
что добавляемая рыночная система имеет положительное арифметическое математическое ожидание. Вспомним первый пример из этого раздела, когда 2 рыночные системы имели нулевой коэффициент корреляции. Эта рыночная система увеличила счет 100 единиц до 156,86 после 4 игр при среднем геометрическом (156,86/ / 100) ^ (1/4) = 1,119. Теперь давайте рассмотрим случай, когда коэффициент корреляции равен -1,00. Так как при таком сценарии никогда не бывает проигрышной игры, оптимальная сумма ставки является бесконечно большой суммой (другими словами, следует ставить 1 единицу на бесконечно малую сумму баланса счета). Для примера мы сделаем 1 ставку на каждые 4 единицы на счете и посмотрим на полученные результаты:

Из этого раздела можно сделать два вывода. Первый состоит в том, что при одновременных ставках или торговле портфелем существует небольшая потеря эффективности, вызванная невозможностью рекапитализировать счет после каждой отдельной игры. Второй заключается в том, что комбинирование ры- ночных систем, при условии, что они имеют положительные математические ожидания (даже если они положительно коррелированы), никогда не уменьшит ваш общий рост за определенный период времени. Однако когда вы продолжаете добавлять все больше и больше рыночных систем, эффективность уменьшается. Если у вас есть, скажем, 10 рыночных систем, и все они одновременно несут убытки, совокупный убыток может уничтожить весь счет, так как вы не сможете уменьшить размер каждого проигрыша, как в случае последовательных сделок. Таким образом, при добавлении новой рыночной системы в портфель польза будет только в двух случаях: когда рыночная система имеет коэффициент корреляции меньше 1 и положительное математическое ожидание или же когда система имеет отрицательное ожидание, но достаточно низкую корреляцию с другими составляющими портфеля, чтобы компенсировать отрицательное ожидание. Каждая добавленная рыночная система вносит постепенно уменьшающийся вклад в среднее геометрическое. То есть каждая новая рыночная система улучшает среднее геометрическое все в меньшей и меньшей степени. Более того, когда вы добавляете новую рыночную систему, теряется общая эффективность из-за одновременных, а не последовательных результатов. В некоторой точке добавление еще одной рыночной системы принесет больше вреда, чем пользы.
Давайте вернемся к нашей игре с броском монеты 2:1. Допустим, мы собираемся одновременно сыграть в две игры: А и Б, — и существует нулевая корреляция между результатами этих двух игр. Оптимальные f для такого случая соответству- ют ставке в 1 единицу на каждые 4,347826 единицы на балансе счета, когда игры проводятся одновременно. Отметьте, что при начальном счете в 100 единиц мы заканчиваем с результатом в 156,86 единицы:
Теперь давайте рассмотрим систему В. Она будет такой же, как система А и Б, только мы будем играть в эту игру без одновременного ведения другой игры. Мы сыграем 8 раз, но не 2 игры по 4 раза, как в прошлом примере. Теперь наше оптимальное f - это ставка 1 единицы на каждые 4 единицы на балансе счета. Мы, как и прежде, имеем те же 8 сделок, но лучший конечный результат (Таблица VI). Мы получили лучший конечный результат не потому, что оптимальные f немного отличаются (оба значения f находятся на соответствующих оптимальных уровнях), а потому, что есть небольшая потеря эффективности при одновременных ставках. Неэффективность является результатом невозможности изменения структуры вашего счета (т.е. рекапитализации) после каждой отдельной ставки, как в игре только по одной рыночной системе. В случае с двумя одновременными
ставками вы можете рекапитализировать счет только 3 раза, в то время как в слу- чае с 8 отдельными ставками вы рекапитализируете счет 7 раз. Отсюда возникает потеря эффективности при одновременных ставках (или при торговле портфелем рыночных систем).
Мы рассмотрели случай, когда одновременные ставки не были коррелирова-ны. Давайте посмотрим, что произойдет при положительной корреляции (+1,00):
Отметьте, что после 4 одновременных игр при корреляции между рыночными системами +1,00 мы увеличили первоначальный счет 100 единиц до 126,56. Это соответствует TWR = 1,2656, или среднему геометрическому (даже если это ком- бинированные игры) 1,2656 ^ (1/4) =1,06066. Теперь вернемся к случаю с одной ставкой. Обратите внимание, что после 4 игр мы получим 126,56 при начальном счете в 100 единиц. Таким образом, среднее геометрическое равно 1,06066. Это говорит о том, что скорость роста такая же, как и при торговле с оптимальными долями на абсолютно коррелированных рынках. Как только коэффициент корреляции опускается ниже +1,00, скорость роста повышается. Таким образом, мы можем утверждать, что при комбинировании рыночных систем ваша скорость роста никогда не будет меньше, чем в случае одиночной ставки по каждой системе, независимо от того, насколько высоки корреляции, при условии,
что добавляемая рыночная система имеет положительное арифметическое математическое ожидание. Вспомним первый пример из этого раздела, когда 2 рыночные системы имели нулевой коэффициент корреляции. Эта рыночная система увеличила счет 100 единиц до 156,86 после 4 игр при среднем геометрическом (156,86/ / 100) ^ (1/4) = 1,119. Теперь давайте рассмотрим случай, когда коэффициент корреляции равен -1,00. Так как при таком сценарии никогда не бывает проигрышной игры, оптимальная сумма ставки является бесконечно большой суммой (другими словами, следует ставить 1 единицу на бесконечно малую сумму баланса счета). Для примера мы сделаем 1 ставку на каждые 4 единицы на счете и посмотрим на полученные результаты:
Из этого раздела можно сделать два вывода. Первый состоит в том, что при одновременных ставках или торговле портфелем существует небольшая потеря эффективности, вызванная невозможностью рекапитализировать счет после каждой отдельной игры. Второй заключается в том, что комбинирование ры- ночных систем, при условии, что они имеют положительные математические ожидания (даже если они положительно коррелированы), никогда не уменьшит ваш общий рост за определенный период времени. Однако когда вы продолжаете добавлять все больше и больше рыночных систем, эффективность уменьшается. Если у вас есть, скажем, 10 рыночных систем, и все они одновременно несут убытки, совокупный убыток может уничтожить весь счет, так как вы не сможете уменьшить размер каждого проигрыша, как в случае последовательных сделок. Таким образом, при добавлении новой рыночной системы в портфель польза будет только в двух случаях: когда рыночная система имеет коэффициент корреляции меньше 1 и положительное математическое ожидание или же когда система имеет отрицательное ожидание, но достаточно низкую корреляцию с другими составляющими портфеля, чтобы компенсировать отрицательное ожидание. Каждая добавленная рыночная система вносит постепенно уменьшающийся вклад в среднее геометрическое. То есть каждая новая рыночная система улучшает среднее геометрическое все в меньшей и меньшей степени. Более того, когда вы добавляете новую рыночную систему, теряется общая эффективность из-за одновременных, а не последовательных результатов. В некоторой точке добавление еще одной рыночной системы принесет больше вреда, чем пользы.
Вложения
FXWizard
Гуру форума
Время, необходимое для достижения определенной цели, и проблема дробного f
Допустим, мы знаем среднее арифметическое HPR и среднее геометрическое HPR для данной системы. Мы можем определить стандартное отклонение HPR из формулы для расчета оценочного среднего геометрического:

где AHPR = среднее арифметическое HPR;
SD = стандартное отклонение значений HPR.
Поэтому мы можем рассчитать стандартное отклонение SD следующим образом:

Возвращаясь к нашей игре с броском монеты 2:1, где математическое ожидание 0,50 долларов и оптимальное f- ставка в 1 доллар на каждые 4 доллара на счете, мы получим среднее геометрическое 1,06066. Для определения среднего арифметического HPR можно использовать уравнение (2.05):

где AHPR = среднее арифметическое HPR;
МО = арифметическое математическое ожидание в единицах; f$= наибольший проигрыш/-f
f = оптимальное f (от 0 до 1).
Таким образом, среднее арифметическое HPR равно:
AHPR =1+(0,5/(-1/-0,25)) =1+(0,5/4) =1+0,125 =1,125
Теперь, так как у нас есть AHPR и EGM, мы можем использовать уравнение (2.04) для определения оценочного стандартного отклонения HPR:

=1,125 ^2- 1,06066 ^62
= 1,265625-1,124999636 =0,140625364
Таким образом, SD ^ 2, то есть дисперсия HPR, равна 0,140625364. Извлекая квад- ратный корень из этой суммы, мы получаем стандартное отклонение HPR =0,140625364 ^(1/2) =0,3750004853. Следует отметить, что это оценочное стандартное отклонение, так как при его расчете используется оценочное среднее геометрическое. Это не совсем точный расчет, но вполне приемлемый для наших целей. Предположим, мы хотим преобразовать значения для стандартного отклонения (или дисперсии), арифметического и среднего геометрического HPR, чтобы отражать торговлю не оптимальным f, а некоторой его частью. Эти преобразования даны далее:
(2.07) FSD = SD * FRAC
(2.08) FGHPR= (FAHPR ^ 2 - FSD ^ 2) А^(1/2),
где FRAC = используемая дробная часть оптимального f; АН PR= среднее арифметическое HPR при оптимальном f; SD = стандартное отклонение HPR при оптимальном f; FAHPR== среднее арифметическое HPR при дробном f; FSD = стандартное отклонение HPR при дробном f; FGHPR = среднее геометрическое HPR при дробном f.

Например, мы хотим посмотреть, какие значения приняли бы FAHPR, FGHPR и FSD в игре с броском монеты 2:1 при половине оптимального f (FRAC = 0,5). Мы знаем, что AHPR= 1,125 и SD = 0,3750004853. Таким образом:

Для оптимального f= 0,25 (1 ставка на каждые 4 доллара на счете) мы получаем значения 1,125, 1,06066 и 0,3750004853 для среднего арифметического, среднего геометрического и стандартного отклонения HPR соответственно. При дробном (0,5) f =0,125 (1 ставка на каждые 8 долларов на счете) мы получаем значения 1,0625, 1,04582499 и 0,1875002427 для среднего арифметического, среднего гео- метрического и стандартного отклонения HPR соответственно. Посмотрим, что происходит, когда мы используем стратегию дробного f. Мы уже знаем, что при дробном f заработаем меньше, чем при оптимальном f. Более того, мы определили, что проигрыши и дисперсии прибылей будут меньше при дробном f. Что произойдет со временем, необходимым для достижения определенной цели?
Мы можем определить только ожидаемое количество сделок, необходимое для достижения определенной цели. Это не то же самое, что ожидаемое время, требуемое для достижения определенной цели, но, так как наши измерения производятся в сделках, мы будем считать время и количество сделок синонимами.
(2.09) N = 1п(Цель) / 1n(Среднее геометрическое),
где N = ожидаемое количество сделок для достижения цели;
Цель = цель в виде множителя первоначального счета, т.е. TWR;
1n() = функция натурального логарифма.
Вернемся к нашему примеру с броском монеты 2:1. При оптимальном f среднее геометрическое равно 1,06066, а при половине f оно составляет 1,04582499. Теперь давайте рассчитаем ожидаемое количество сделок, необходимое для удвоения на- шего счета (Цель = 2). При полном f:
N=ln(2)/ln( 1,06066) =0,6931471/0,05889134 =11,76993
Таким образом, в игре с броском монеты 2:1 при полном f следует ожидать 11,76993 сделок для удвоения нашего счета. При половине f получаем:
N=ln(2)/ln( 1,04582499) =0,6931471/0,04480602 = 15,46996
Таким образом, при половине f мы ожидаем, что потребуется 15,46996 сделок для удвоения счета. Другими словами, чтобы достичь цели при торговле на уровне f/ /2, от нас понадобится на 31,44% сделок больше. Ну что же, это звучит не так уж плохо. Проявляя терпение для достижения поставленной цели, мы потратим времени на 31,44% больше, но сократим худший проигрыш и дисперсию наполовину. Согласитесь, половина — это довольно много. Чем меньшую часть оптимального f вы будете использовать, тем более гладкую кривую счета получите, и тем меньшее время вы будете в проигрыше. Теперь посмотрим на эту ситуацию с другой стороны. Допустим, вы открываете два счета: один для торговли с полным f и один для торговли с половиной f. После 12 игр ваш счет с полным f увеличится в 2,02728259 в 12 раза. После 12 сделок (с половиной f) он вырастет в 1,712017427 (1,04582499 ^ 12) раза. С половиной f первоначальный счет увеличится в 2,048067384 (1,04582499 ^ 16) раза при 16 сделках. Поэтому, торгуя на одну треть дольше, вы достигнете той же цели, что и при полном оптимальном f, но при активности, меньшей наполовину. Однако к 16 сделке счет с полным f будет в 2,565777865 (1,06066 ^ 16) раза больше вашего первоначального счета. Полное f продолжает увеличивать счет. К 100 сделке ваш счет с половиной f увеличится в 88,28796546 раз, но полное f увеличит его в 361,093016 раз!
Единственный минус торговли с дробным f— это большее время, необходимое для достижения определенной цели. Все дело во времени. Мы можем вложить деньги в казначейские обязательства и достичь-таки заданной цели через определенное время с минимальными промежуточными падениями баланса и дисперсией! Время — это суть проблемы.
Допустим, мы знаем среднее арифметическое HPR и среднее геометрическое HPR для данной системы. Мы можем определить стандартное отклонение HPR из формулы для расчета оценочного среднего геометрического:
где AHPR = среднее арифметическое HPR;
SD = стандартное отклонение значений HPR.
Поэтому мы можем рассчитать стандартное отклонение SD следующим образом:
Возвращаясь к нашей игре с броском монеты 2:1, где математическое ожидание 0,50 долларов и оптимальное f- ставка в 1 доллар на каждые 4 доллара на счете, мы получим среднее геометрическое 1,06066. Для определения среднего арифметического HPR можно использовать уравнение (2.05):
где AHPR = среднее арифметическое HPR;
МО = арифметическое математическое ожидание в единицах; f$= наибольший проигрыш/-f
f = оптимальное f (от 0 до 1).
Таким образом, среднее арифметическое HPR равно:
AHPR =1+(0,5/(-1/-0,25)) =1+(0,5/4) =1+0,125 =1,125
Теперь, так как у нас есть AHPR и EGM, мы можем использовать уравнение (2.04) для определения оценочного стандартного отклонения HPR:
=1,125 ^2- 1,06066 ^62
= 1,265625-1,124999636 =0,140625364
Таким образом, SD ^ 2, то есть дисперсия HPR, равна 0,140625364. Извлекая квад- ратный корень из этой суммы, мы получаем стандартное отклонение HPR =0,140625364 ^(1/2) =0,3750004853. Следует отметить, что это оценочное стандартное отклонение, так как при его расчете используется оценочное среднее геометрическое. Это не совсем точный расчет, но вполне приемлемый для наших целей. Предположим, мы хотим преобразовать значения для стандартного отклонения (или дисперсии), арифметического и среднего геометрического HPR, чтобы отражать торговлю не оптимальным f, а некоторой его частью. Эти преобразования даны далее:
(2.07) FSD = SD * FRAC
(2.08) FGHPR= (FAHPR ^ 2 - FSD ^ 2) А^(1/2),
где FRAC = используемая дробная часть оптимального f; АН PR= среднее арифметическое HPR при оптимальном f; SD = стандартное отклонение HPR при оптимальном f; FAHPR== среднее арифметическое HPR при дробном f; FSD = стандартное отклонение HPR при дробном f; FGHPR = среднее геометрическое HPR при дробном f.

Например, мы хотим посмотреть, какие значения приняли бы FAHPR, FGHPR и FSD в игре с броском монеты 2:1 при половине оптимального f (FRAC = 0,5). Мы знаем, что AHPR= 1,125 и SD = 0,3750004853. Таким образом:
Для оптимального f= 0,25 (1 ставка на каждые 4 доллара на счете) мы получаем значения 1,125, 1,06066 и 0,3750004853 для среднего арифметического, среднего геометрического и стандартного отклонения HPR соответственно. При дробном (0,5) f =0,125 (1 ставка на каждые 8 долларов на счете) мы получаем значения 1,0625, 1,04582499 и 0,1875002427 для среднего арифметического, среднего гео- метрического и стандартного отклонения HPR соответственно. Посмотрим, что происходит, когда мы используем стратегию дробного f. Мы уже знаем, что при дробном f заработаем меньше, чем при оптимальном f. Более того, мы определили, что проигрыши и дисперсии прибылей будут меньше при дробном f. Что произойдет со временем, необходимым для достижения определенной цели?
Мы можем определить только ожидаемое количество сделок, необходимое для достижения определенной цели. Это не то же самое, что ожидаемое время, требуемое для достижения определенной цели, но, так как наши измерения производятся в сделках, мы будем считать время и количество сделок синонимами.
(2.09) N = 1п(Цель) / 1n(Среднее геометрическое),
где N = ожидаемое количество сделок для достижения цели;
Цель = цель в виде множителя первоначального счета, т.е. TWR;
1n() = функция натурального логарифма.
Вернемся к нашему примеру с броском монеты 2:1. При оптимальном f среднее геометрическое равно 1,06066, а при половине f оно составляет 1,04582499. Теперь давайте рассчитаем ожидаемое количество сделок, необходимое для удвоения на- шего счета (Цель = 2). При полном f:
N=ln(2)/ln( 1,06066) =0,6931471/0,05889134 =11,76993
Таким образом, в игре с броском монеты 2:1 при полном f следует ожидать 11,76993 сделок для удвоения нашего счета. При половине f получаем:
N=ln(2)/ln( 1,04582499) =0,6931471/0,04480602 = 15,46996
Таким образом, при половине f мы ожидаем, что потребуется 15,46996 сделок для удвоения счета. Другими словами, чтобы достичь цели при торговле на уровне f/ /2, от нас понадобится на 31,44% сделок больше. Ну что же, это звучит не так уж плохо. Проявляя терпение для достижения поставленной цели, мы потратим времени на 31,44% больше, но сократим худший проигрыш и дисперсию наполовину. Согласитесь, половина — это довольно много. Чем меньшую часть оптимального f вы будете использовать, тем более гладкую кривую счета получите, и тем меньшее время вы будете в проигрыше. Теперь посмотрим на эту ситуацию с другой стороны. Допустим, вы открываете два счета: один для торговли с полным f и один для торговли с половиной f. После 12 игр ваш счет с полным f увеличится в 2,02728259 в 12 раза. После 12 сделок (с половиной f) он вырастет в 1,712017427 (1,04582499 ^ 12) раза. С половиной f первоначальный счет увеличится в 2,048067384 (1,04582499 ^ 16) раза при 16 сделках. Поэтому, торгуя на одну треть дольше, вы достигнете той же цели, что и при полном оптимальном f, но при активности, меньшей наполовину. Однако к 16 сделке счет с полным f будет в 2,565777865 (1,06066 ^ 16) раза больше вашего первоначального счета. Полное f продолжает увеличивать счет. К 100 сделке ваш счет с половиной f увеличится в 88,28796546 раз, но полное f увеличит его в 361,093016 раз!
Единственный минус торговли с дробным f— это большее время, необходимое для достижения определенной цели. Все дело во времени. Мы можем вложить деньги в казначейские обязательства и достичь-таки заданной цели через определенное время с минимальными промежуточными падениями баланса и дисперсией! Время — это суть проблемы.
Вложения
FXWizard
Гуру форума
Сравнение торговых систем
Мы увидели, что две торговые системы можно сравнивать на основе их средних геометрических при соответствующих оптимальных f. Далее, мы можем сравнивать системы, основываясь на том, насколько высокими являются их оптимальные f, поскольку более высокие оптимальные f соответствуют более рискованным системам. Это связано с тем, что исторический проигрыш может понизить счет, по крайней мере, на процент f. Поэтому существуют две основные величины для сравнения систем: среднее геометрическое при оптимальном f, где более высокое среднее геометрическое предпочтительнее, и само оптимальное f, где более низкое оптимальное f лучше. Таким образом, вместо одной величины для измерения эффективности системы мы получаем две; эффективность должна измеряться в двухмерном пространстве, где одна ось является средним геометрическим, а другая — значением f. Чем выше среднее геометрическое при оптимальном f, тем лучше система. Также чем ниже оптимальное f, тем лучше система.
Среднее геометрическое ничего не скажет нам о проигрыше. Высокое среднее геометрическое не означает, что проигрыш системы большой (или, наоборот, незначительный). Среднее геометрическое имеет отношение только к прибыли. Оптимальное f является мерой минимального ожидаемого исторического проигрыша как процентное понижение баланса. Более высокое оптимальное f не говорит о более высоком (или низком) доходе. Мы можем также использовать эти положения для сравнения определенной системы при дробном значении f с другой системой при полном значении оптимального f. При рассмотрении систем вам следует учитывать, насколько высоки средние геометрические и каковы оптимальные f. Например, у нас есть система А, которая имеет среднее геометрическое 1,05 и оптимальное f= 0,8. Также у нас есть система В, которая имеет среднее геометрическое 1,025 и оптимальное f=0,4. Система А при половине уровня f будет иметь то же минимальное историческое падение баланса худшего случая (проигрыш) в 40%, как и система В при полном f, но среднее геометрическое системы А при половине f вce равно будет выше, чем среднее геометрическое системы В при полном значении f. Поэтому система А лучше системы В. «Минутку, — можете возразить вы, — разве не является самым важным то обстоятельство, что среднее геометрическое больше 1, и системе необходимо быть только минимально прибыльной, чтобы (посредством грамотного управления деньгами) заработать желаемую сумму!» Так оно и есть. Скорость, с которой вы зарабатываете деньги, является функцией среднего геометрического на уровне используемого f. Ожидаемая дисперсия зависит от того, насколько большое f вы используете. Вы, безусловно, должны иметь систему с оптимальным f и со средним геометрическим, большим 1 (то есть с положительным математическим ожиданием). С такой системой вы можете заработать практически любую сумму через соответствующее количество сделок. Скорость роста (количество сделок, необходимое для достижения определенной цели) зависит от среднего геометрического при используемом значении f. Дисперсия на пути к этой цели также является функцией используемого значения f. Хотя важность среднего геометрического и применяемого f вторична по сравнению с тем фактом, что вы должны иметь положительное математическое ожидание, эти величины действительно полезны при сравнении двух систем или методов, которые имеют положительное математическое ожидание и равную уверенность в их работе в будущем.
Мы увидели, что две торговые системы можно сравнивать на основе их средних геометрических при соответствующих оптимальных f. Далее, мы можем сравнивать системы, основываясь на том, насколько высокими являются их оптимальные f, поскольку более высокие оптимальные f соответствуют более рискованным системам. Это связано с тем, что исторический проигрыш может понизить счет, по крайней мере, на процент f. Поэтому существуют две основные величины для сравнения систем: среднее геометрическое при оптимальном f, где более высокое среднее геометрическое предпочтительнее, и само оптимальное f, где более низкое оптимальное f лучше. Таким образом, вместо одной величины для измерения эффективности системы мы получаем две; эффективность должна измеряться в двухмерном пространстве, где одна ось является средним геометрическим, а другая — значением f. Чем выше среднее геометрическое при оптимальном f, тем лучше система. Также чем ниже оптимальное f, тем лучше система.
Среднее геометрическое ничего не скажет нам о проигрыше. Высокое среднее геометрическое не означает, что проигрыш системы большой (или, наоборот, незначительный). Среднее геометрическое имеет отношение только к прибыли. Оптимальное f является мерой минимального ожидаемого исторического проигрыша как процентное понижение баланса. Более высокое оптимальное f не говорит о более высоком (или низком) доходе. Мы можем также использовать эти положения для сравнения определенной системы при дробном значении f с другой системой при полном значении оптимального f. При рассмотрении систем вам следует учитывать, насколько высоки средние геометрические и каковы оптимальные f. Например, у нас есть система А, которая имеет среднее геометрическое 1,05 и оптимальное f= 0,8. Также у нас есть система В, которая имеет среднее геометрическое 1,025 и оптимальное f=0,4. Система А при половине уровня f будет иметь то же минимальное историческое падение баланса худшего случая (проигрыш) в 40%, как и система В при полном f, но среднее геометрическое системы А при половине f вce равно будет выше, чем среднее геометрическое системы В при полном значении f. Поэтому система А лучше системы В. «Минутку, — можете возразить вы, — разве не является самым важным то обстоятельство, что среднее геометрическое больше 1, и системе необходимо быть только минимально прибыльной, чтобы (посредством грамотного управления деньгами) заработать желаемую сумму!» Так оно и есть. Скорость, с которой вы зарабатываете деньги, является функцией среднего геометрического на уровне используемого f. Ожидаемая дисперсия зависит от того, насколько большое f вы используете. Вы, безусловно, должны иметь систему с оптимальным f и со средним геометрическим, большим 1 (то есть с положительным математическим ожиданием). С такой системой вы можете заработать практически любую сумму через соответствующее количество сделок. Скорость роста (количество сделок, необходимое для достижения определенной цели) зависит от среднего геометрического при используемом значении f. Дисперсия на пути к этой цели также является функцией используемого значения f. Хотя важность среднего геометрического и применяемого f вторична по сравнению с тем фактом, что вы должны иметь положительное математическое ожидание, эти величины действительно полезны при сравнении двух систем или методов, которые имеют положительное математическое ожидание и равную уверенность в их работе в будущем.
FXWizard
Гуру форума
Слишком большая чувствительность к величине наибольшего проигрыша
Недостаток подхода, основанного на оптимальном f, заключается в том, что f слишком зависит от величины наибольшего проигрыша, что является серьезной проблемой для многих трейдеров, и они доказывают, что количество контрактов, которые вы открываете сегодня, не должно быть функцией одной неудачной сделки в прошлом.
Для устранения этой сверхчувствительности к наибольшему проигрышу были разработаны разнообразные алгоритмы. Многие из этих алгоритмов заключаются в изменении наибольшего проигрыша в большую или меньшую сторону, чтобы сделать наибольший проигрыш функцией текущей волатильности рынка. Эта связь, как утверждают некоторые, квадратичная, то есть абсолютное значение наибольшего проигрыша, по всей видимости, увеличивается с большей скоростью, чем волатильность. Волатильность чаще всего определяется как средний дневной диапазон цен за последние несколько недель или как среднее абсолютное дневное изменение за последние несколько недель. Однако об этой зависимости нельзя говорить с полной уверенностью. То, что волатильность сегодня составляет X, не означает, что наш наибольший проигрыш будет Х ^ Y. Можно говорить лишь о том, что он обычно где-то около Х ^ Y. Если бы мы могли заранее определить сегодняшний наибольший проигрыш, то, безусловно, могли бы лучше использовать методы управления деньгами1. Это тот самый случай, когда мы должны рассмотреть сценарий худшего случая и отталкиваться от него. Проблема состоит в том, что мы не знаем точно, каким будет сегодня наибольший проигрыш. Алгоритмы, которые могут спрогнозировать это, не очень эффективны, так как они часто дают ошибочные результаты.
Предположим, в течение торгового дня произошло событие, вызвавшее на рынке шок, и до этого шока волатильность была достаточно низкой. Затем рынок находился не на вашей стороне несколько следующих дней. Или, допустим, на следующий день рынок открылся с огромным разрывом не в вашу пользу. Эти события так же стары, как сама торговля товарами и акциями. Они могут произойти и происходят, и о них не всегда предупреждает заранее повышающаяся волатильность. Таким образом, лучше не «сокращать» ваш наибольший исторический проигрыш для отражения текущего рынка с низкой волатильностью. Более того, есть реальная возможность испытать в будущем проигрыш больший, чем наибольший исторический проигрыш. Наибольший проигрыш, который вы получили в прошлом, может оказаться наибольшим проигрышем, который вы испытаете сегодня, и не зависеть от текущей волатильности1. Проблема состоит в том, что с эмпирической точки зрения f, оптимальное в прошлом, является функцией наибольшего проигрыша в прошлом. С этим ничего не поделаешь. Однако мы увидим, когда перейдем к параметрическим методам, что можно предусмотреть больший проигрыш в будущем. При этом мы будем готовы к появлению почти неизбежного большого проигрыша. Вместо подгонки наибольшего проигрыша к текущей ситуации на рынке, чтобы эмпирическое оптимальное f отражало нынешнюю ситуацию, лучше изучить параметрические методы. Следующий метод является возможным решением данной проблемы и может применяться вне зависимости от того, рассчитываем мы оптимальное f эмпирически или параметрически.
1 Именно в этом случае использование опционов в торговой стратегии столь полезно. Покупка пут или коллопциона в обратном направлении от позиции по базовому инструменту для ограничения проигрыша либо торговля опционами вместо базового инструмента дадут вам заранее известный максимальный проигрыш, что очень пригодится в управлении деньгами, особенно при оптимальном f. Более того, если вы знаете заранее, каким будет ваш максимальный проигрыш (например, при дневной торговле), тогда вы всегда сможете точно определить величину f в долларах для каждой сделки как следующую дробь: риск в долларах на единицу/оптимальное f. Например, дневной трейдер знает, что его оптимальное f =0,4. Его стоп (stop-loss) сегодня на основе 1 единицы равен 900 долларам. Поэтому оптимально торговать 1 единицей на каждые 2250 долларов ($900 / 0,4) на балансе счета.

Недостаток подхода, основанного на оптимальном f, заключается в том, что f слишком зависит от величины наибольшего проигрыша, что является серьезной проблемой для многих трейдеров, и они доказывают, что количество контрактов, которые вы открываете сегодня, не должно быть функцией одной неудачной сделки в прошлом.
Для устранения этой сверхчувствительности к наибольшему проигрышу были разработаны разнообразные алгоритмы. Многие из этих алгоритмов заключаются в изменении наибольшего проигрыша в большую или меньшую сторону, чтобы сделать наибольший проигрыш функцией текущей волатильности рынка. Эта связь, как утверждают некоторые, квадратичная, то есть абсолютное значение наибольшего проигрыша, по всей видимости, увеличивается с большей скоростью, чем волатильность. Волатильность чаще всего определяется как средний дневной диапазон цен за последние несколько недель или как среднее абсолютное дневное изменение за последние несколько недель. Однако об этой зависимости нельзя говорить с полной уверенностью. То, что волатильность сегодня составляет X, не означает, что наш наибольший проигрыш будет Х ^ Y. Можно говорить лишь о том, что он обычно где-то около Х ^ Y. Если бы мы могли заранее определить сегодняшний наибольший проигрыш, то, безусловно, могли бы лучше использовать методы управления деньгами1. Это тот самый случай, когда мы должны рассмотреть сценарий худшего случая и отталкиваться от него. Проблема состоит в том, что мы не знаем точно, каким будет сегодня наибольший проигрыш. Алгоритмы, которые могут спрогнозировать это, не очень эффективны, так как они часто дают ошибочные результаты.
Предположим, в течение торгового дня произошло событие, вызвавшее на рынке шок, и до этого шока волатильность была достаточно низкой. Затем рынок находился не на вашей стороне несколько следующих дней. Или, допустим, на следующий день рынок открылся с огромным разрывом не в вашу пользу. Эти события так же стары, как сама торговля товарами и акциями. Они могут произойти и происходят, и о них не всегда предупреждает заранее повышающаяся волатильность. Таким образом, лучше не «сокращать» ваш наибольший исторический проигрыш для отражения текущего рынка с низкой волатильностью. Более того, есть реальная возможность испытать в будущем проигрыш больший, чем наибольший исторический проигрыш. Наибольший проигрыш, который вы получили в прошлом, может оказаться наибольшим проигрышем, который вы испытаете сегодня, и не зависеть от текущей волатильности1. Проблема состоит в том, что с эмпирической точки зрения f, оптимальное в прошлом, является функцией наибольшего проигрыша в прошлом. С этим ничего не поделаешь. Однако мы увидим, когда перейдем к параметрическим методам, что можно предусмотреть больший проигрыш в будущем. При этом мы будем готовы к появлению почти неизбежного большого проигрыша. Вместо подгонки наибольшего проигрыша к текущей ситуации на рынке, чтобы эмпирическое оптимальное f отражало нынешнюю ситуацию, лучше изучить параметрические методы. Следующий метод является возможным решением данной проблемы и может применяться вне зависимости от того, рассчитываем мы оптимальное f эмпирически или параметрически.
1 Именно в этом случае использование опционов в торговой стратегии столь полезно. Покупка пут или коллопциона в обратном направлении от позиции по базовому инструменту для ограничения проигрыша либо торговля опционами вместо базового инструмента дадут вам заранее известный максимальный проигрыш, что очень пригодится в управлении деньгами, особенно при оптимальном f. Более того, если вы знаете заранее, каким будет ваш максимальный проигрыш (например, при дневной торговле), тогда вы всегда сможете точно определить величину f в долларах для каждой сделки как следующую дробь: риск в долларах на единицу/оптимальное f. Например, дневной трейдер знает, что его оптимальное f =0,4. Его стоп (stop-loss) сегодня на основе 1 единицы равен 900 долларам. Поэтому оптимально торговать 1 единицей на каждые 2250 долларов ($900 / 0,4) на балансе счета.