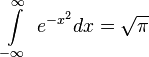число пи это фундамент математики
это основа
это самая суть
смешки тут неуместны
а еще нельзя забывать о числе е
это все взаимосвязано
великие таинства стоят за этим
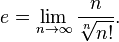
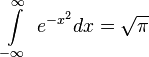
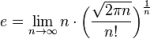
кроме того!
в бинарном представлении числа пи есть тексты
можно найти любой - подчеркнём! - любой осмысленный текст
в том числе верно то что среди последовательностей можно найти грааль
причем не только описание грааля но и mql-советник и даже готовые сеты
число пи содержит вообще всё
Пи - это отношение длины окружности к ее диаметру. В конце 18 века Ламберт и Лежандр установили, что pi - иррациональное число, а в 19 веке Линдеман доказал, что оно трансцендентное. В процессе вычислений этих самых знаков было открыто множество разных научных методов и целых наук. Но самое главное – в десятичной части числа пи нет повторений, как в обычной периодической дроби, а число знаков после запятой у него – бесконечно. На сегодняшний день проверено, что в 500 млрд. знаков числа пи повторений действительно нет. Есть основания полагать, что их нет вообще.
Поскольку в последовательности знаков числа пи нет повторений – это значит, что последовательность знаков числа пи подчиняется теории хаоса, точнее, число пи – это и есть
хаос, записанный цифрами. Более того, при желании, можно этот хаос представить графически, и есть предположение, что этот Хаос разумен. В 1965-м году американский математик М. Улэм, сидя на одном скучном собрании, от нечего делать начал писать на клетчатой бумаге цифры, входящие в число пи. Поставив в центре 3 и двигаясь по спирали против часовой стрелки, он выписывал 1, 4, 1, 5, 9, 2, 6, 5 и прочие цифры после запятой. Попутно он обводил все простые числа кружками. Каково же было его
удивление и ужас, когда кружки стали выстраиваться вдоль прямых!
Двое математиков - Дэвид Бэйли (Lawrence Berkeley NL, Калифорния) и Ричард Крандалл (Reed College, Орегон) - сделали важный шаг в строгом доказательстве* того, что
pi содержит не какое-то одно сообщение, а вообще любое (в том числе и любое осмысленное). Является ли разложение pi случайным или упорядоченным - это одна из труднейших проблем математики. Бэйли и Крандалл показали, что
нормальность pi будет строго установлена, если удастся доказать теорему из совсем другой области -
теории хаоса. "Мы не доказали нормальности pi, но мы нашли путь к этому," - говорит Бэйли. Пройти эту дорогу до конца может быть и трудно, но он надеется доказать по крайней мере упрощенную гипотезу о хаосе в течение нескольких лет.
_________________________
* Bailey, D. and Crandall, R. On the random character of fundamental constant expansion. Experimental Mathematics, 10, 175 - 190, (2001).