Дневник начинающей фундаменталистки

[Olchik]

Зачем смотреть на распределения?​

Я смотрю на рынок через распределения доходностей, вот такая у меня фишка. Но не для того, чтобы, взглянув на распределение, выстроить торговую стратегию, а для того, чтобы взглянуть на рынок «с расстояния», ведь большое видится на расстоянии (С). Через распределение я понимаю, каков рынок в среднем, точнее его структурная волатильность. Для меня это способ обобщить, понять пределы фонового шума и наметить границы возможного.

Долгое время я считала этот подход интуитивным, почти личным. Но позже обнаружила, что в научной среде споры о форме распределения доходностей идут давно. Одни исследователи обобщают его до нормального, другие - до распределения Коши, которое не имеет конечного математического ожидания и дисперсии, что делает традиционную статистику неприменимой. И каждый через форму распределения пытается ответить на фундаментальные вопросы: как моделировать риски, можно ли систематически побеждать рынок, учитывая его аномалии, и как строить практические стратегии для торговли и инвестиций?

То есть распределение становится не просто инструментом анализа, а аргументом в споре о природе рынка, который сочетает теорию с практикой. Мотивация исследователей часто лежит в эмпирических данных: реальные доходности акций показывают жирные хвосты (крайние события, как крахи), асимметрию и отклонения от простых моделей, что требует новых подходов для расчета рисков (например, Value at Risk) или ценообразования опционов (как в модели Блэка-Шоулза). Это не только философия, но и экономическая необходимость: для банков - оценка капитала под риски, для трейдеров - хеджирование, для регуляторов - стабильность системы. Если распределение нормально, значит, рынок относительно симметричен в рисках и поддается классическим стратегиям, хотя эмпирика показывает асимметрию. Если логнормально, значит, рост возможен, но асимметричен с акцентом на положительный дрейф. А если это распределение Коши, то рынок хаотичен, с бесконечной дисперсией, и идея устойчивой прибыли теряет смысл, подчеркивая роль "черных лебедей".

В истории финансовой математики предлагались и другие формы распределений, эволюционирующие от простых к сложным, чтобы лучше соответствовать данным. Например, стабильные распределения Леви обобщают Коши, учитывая параметр стабильности для жирных хвостов. T-распределение предлагает компромисс с конечной дисперсией, но тяжелыми хвостами, подходящее для моделирования волатильности в GARCH. Талеб указывает на power-law распределение (на основе идей Pareto и Mandelbrot) как на ключевое для описания редких, но разрушительных событий. Гиперболические леви-процессы Эрнста Эберлейна для моделирования скачков и асимметрии в волатильных активах, как крипта.

Но мой интерес не в выборе "правильной" формы, а в том, чтобы использовать распределение как диагностический фильтр. Я не стремлюсь к постоянной торговле, наоборот, наблюдаю, выжидаю и действую лишь тогда, когда рынок выходит из режима мелкого шума. Это не претензия на новацию, а один из моих способов навигации в среде высокой неопределенности, где распределение становится инструментом проверки: удалось ли мне отделить шум от сигнала.

Ниже распределение дневных доходностей американского фондового индекса SP500: вертикальной гистограммой реальное рыночное, оранжевой кривой – нормальное (гауссово):



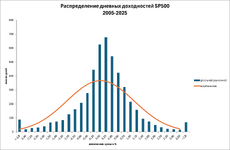
Доходность рассчитана как внутридневное изменение:

((close−open)/open)×100

то есть без учета межсессионных гэпов.

Визуально видно, что у реального рыночного распределения существенно выше пик в центре, чем у нормального. Это говорит о том, что большинство дней малоподвижные, то есть рынок почти всегда находится в состоянии низкой волатильности, в связи с чем заработать на нем так сложно. Хвосты реального распределения (отклонения выше ±2.6%) заметно выше, чем у нормального, что говорит о том, что экстремальные события происходят чаще, чем предсказывает теория. Однако реальные хвосты еще тяжелее, так как я выбросила из расчета межсессионные гепы. Это важно для оценки риска: классические модели недооценивают вероятность краха или резкого роста. Легкое смещение центра вправо придает распределению асимметрию, что отражает долгосрочный восходящий тренд американского рынка.

Если более количественно описать несовпадение между реальным распределением доходностей и прикинуть доли попадания в диапазоны ±1σ, ±2σ, ±3σ исходя из значений среднего (0.03%) и стандартного отклонения (1.08%) реального рыночного распределения, то получится примерно такая сравнительная табличка:

Интервал	Реальное распределение	Теоретическое (нормальное)	Вывод
±1σ	~79.8%	68.2%	Центр более "зажат"
±2σ	~95.1%	95.4%	Почти совпадает, но хвосты начинаются
±3σ	~99.0%	99.7%	Хвосты тяжелее, экстремумы чаще

Важное уточнение.

Я не математик и не ученый, и ни в коем случае не претендую на научность, чтобы вам там не показалось. Мне пришлось вникнуть во все это не из академического интереса, а из практической усталости: в какой-то момент мне надоел бесконечный бег по замкнутому кругу перебора эмпирических моделей под текущее состояние рынка. Я не отрицаю эмпирику, в ряде случаев она очень полезна. Единственное, что я не делаю - не строю стратегии исключительно на ее основе. Например, то же распределение доходностей – это эмпирика, но на макроуровне, она не раздает рецепты, а просто описывает контекст в самом общем смысле. Эмпирика полезна для обобщений, но не для стратегий без контекста событий, потому что катализатором хвостовых событий становятся не графические паттерны любой степени сложности, а реальные события, например приход новой информации, не совпадающей с ожиданиями рынка.

Паттерн - не причина скачка волатильности. Он может ей предшествовать, может ее сопровождать, но после не значит вследствие. Считаю это ключевой ошибкой тех, кто торгует исключительно по эмпирике или по цифрам из опционных отчетов, не понимая, что стоит за этими цифрами. Например, если цена уходит от страйка с высоким открытым интересом, это интерпретируют как «кукл увел цену, чтобы не переплатить на экспирации». Но рынок возвращается не потому, что кто-то его отвел, а потому, что он таков по своей природе. Закрой завтра все биржи, предлагающие торговлю опционами, это ничего не изменит. Рынок все равно будет возвращаться. Один чаще, другой реже.

 

[Olchik]

Хвосты распределения​

Когда-то мне казалось логичным, что если подавляющее большинство рыночных движений сосредоточено в центре распределения, и цена скорее всего завтра будет близка к сегодняшней, то разумнее ловить рыночный шум, а не охотиться за редкими импульсами. В таком подходе есть своя рациональность. Скальперские техники, например, способны извлекать немалую прибыль из почти гарантированных микродвижений, пусть даже всего в пару пипсов.

Однако со временем мне стало понятно, что ловля шума требует решения более сложной задачи, в которой нужно быть уверенной, что хвост точно не прилетит. Это куда сложнее, чем просто ждать его появления и пытаться на нем прокатиться. Как бы заманчиво ни выглядела теория, но практика подсказывала, что необходимо двигаться от мысли «как не попасть на хвост» к мысли «как в него попасть». Путем экспериментов я выяснила, если сосредоточиться на ловле редких, но достаточно продолжительных импульсов, можно подобрать фильтры для открытия позиций, с помощью которых точность попадания в хвост распределения окажется неожиданно высокой. Да, подобные движения случаются редко, но дают более ощутимый и (что особенно важно) стабильный результат в плане роста кривой эквити.

Хотя это мой опыт, у вас он может быть другим.

Чтобы ловить импульсы, важно понимать, какие внешние драйверы обычно их запускают. И здесь тоже важно отойти от того, как думают все, и как это кажется со стороны. Вот вам простой пример.

Ниже два распределения дневных доходностей индекса S&P 500, совмещенные в комбинированной диаграмме. Первое вы уже видели в предыдущем сообщении (синяя диаграмма), а во второе (оранжевая диаграмма) я добавила фильтр - в выборку попали не все дни, а лишь определенные. Ну и естественно частотность дней (ось Y) я перевела в %, чтобы их можно было сравнить количественно и визуально.



В оранжевом распределении наблюдаются умеренные сдвиги по сравнению с исходным синим:

• центр распределения стал менее выраженным: количество дней с доходностью около нуля немного сократилось, что может указывать на повышенную направленность движения в отобранных днях;
• хвосты распределения слегка утолщились: увеличилась доля дней с доходностью выше ±1.4%, особенно в положительном направлении, что говорит о повышенной вероятности импульсных движений;
• асимметрия стала чуть заметнее: положительные доходности в отфильтрованных днях проявляются с большей частотой, чем отрицательные, хотя этот эффект не является доминирующим.

Однако, несмотря на эти изменения, общая форма распределения осталась близкой к первоначальной. Центр по-прежнему содержит основную массу наблюдений, а экстремальные значения остаются редкими. Это говорит о том, что фильтр, примененный к выборке, не сумел радикально изменить форму распределения, а лишь слегка сместил акценты. Хотя иногда и этого бывает достаточно, но хотелось бы явно большего.

Итак, чуда не случилось. Распределение стало немного более импульсным, однако не вышло за рамки типичной рыночной статистики. Теперь я вам открою секрет, какой фильтр был использован: в оранжевое распределение попали только дни публикации NFP. Казалось бы, что может сильнее тряхнуть рынок, чем выход столь важной экономической статистики? Я часто читаю рассуждения других трейдеров, которые уверены в том, что стоит только торговать в день NFP, и будет им счастье. К сожалению, это так просто не работает. Хотя по себе знаю (по своей статистике), что NFP, действительно, хорошие дни для ловли импульсов. Однако одного фильтра «я буду торговать в такие дни» недостаточно, чтобы разбить центр распределения. Это не магическая кнопка. Чтобы фильтр работал, он должен менять форму распределения, а не просто соответствовать нашим ожиданиям.

ПС
Думаю, теперь вам стало понятнее, как именно я подхожу к анализу методов, которые использую для подбора фильтров входа в позицию: я сравниваю, как они влияют на форму распределения, и сразу вижу, насколько выбранный мною фильтр - это не просто попытка выдать желаемое за действительное, а статистически обоснованный инструмент.

 

[Sergerk]

Хвосты распределения​

Когда-то мне казалось логичным, что если подавляющее большинство рыночных движений сосредоточено в центре распределения, и цена скорее всего завтра будет близка к сегодняшней, то разумнее ловить рыночный шум, а не охотиться за редкими импульсами. В таком подходе есть своя рациональность. Скальперские техники, например, способны извлекать немалую прибыль из почти гарантированных микродвижений, пусть даже всего в пару пипсов.

Однако со временем мне стало понятно, что ловля шума требует решения более сложной задачи, в которой нужно быть уверенной, что хвост точно не прилетит. Это куда сложнее, чем просто ждать его появления и пытаться на нем прокатиться. Как бы заманчиво ни выглядела теория, но практика подсказывала, что необходимо двигаться от мысли «как не попасть на хвост» к мысли «как в него попасть». Путем экспериментов я выяснила, если сосредоточиться на ловле редких, но достаточно продолжительных импульсов, можно подобрать фильтры для открытия позиций, с помощью которых точность попадания в хвост распределения окажется неожиданно высокой. Да, подобные движения случаются редко, но дают более ощутимый и (что особенно важно) стабильный результат в плане роста кривой эквити.

Хотя это мой опыт, у вас он может быть другим.

Чтобы ловить импульсы, важно понимать, какие внешние драйверы обычно их запускают. И здесь тоже важно отойти от того, как думают все, и как это кажется со стороны. Вот вам простой пример.

Ниже два распределения дневных доходностей индекса S&P 500, совмещенные в комбинированной диаграмме. Первое вы уже видели в предыдущем сообщении (синяя диаграмма), а во второе (оранжевая диаграмма) я добавила фильтр - в выборку попали не все дни, а лишь определенные. Ну и естественно частотность дней (ось Y) я перевела в %, чтобы их можно было сравнить количественно и визуально.

Посмотреть вложение 575085

В оранжевом распределении наблюдаются умеренные сдвиги по сравнению с исходным синим:

• центр распределения стал менее выраженным: количество дней с доходностью около нуля немного сократилось, что может указывать на повышенную направленность движения в отобранных днях;
• хвосты распределения слегка утолщились: увеличилась доля дней с доходностью выше ±1.4%, особенно в положительном направлении, что говорит о повышенной вероятности импульсных движений;
• асимметрия стала чуть заметнее: положительные доходности в отфильтрованных днях проявляются с большей частотой, чем отрицательные, хотя этот эффект не является доминирующим.

Однако, несмотря на эти изменения, общая форма распределения осталась близкой к первоначальной. Центр по-прежнему содержит основную массу наблюдений, а экстремальные значения остаются редкими. Это говорит о том, что фильтр, примененный к выборке, не сумел радикально изменить форму распределения, а лишь слегка сместил акценты. Хотя иногда и этого бывает достаточно, но хотелось бы явно большего.

Итак, чуда не случилось. Распределение стало немного более импульсным, однако не вышло за рамки типичной рыночной статистики. Теперь я вам открою секрет, какой фильтр был использован: в оранжевое распределение попали только дни публикации NFP. Казалось бы, что может сильнее тряхнуть рынок, чем выход столь важной экономической статистики? Я часто читаю рассуждения других трейдеров, которые уверены в том, что стоит только торговать в день NFP, и будет им счастье. К сожалению, это так просто не работает. Хотя по себе знаю (по своей статистике), что NFP, действительно, хорошие дни для ловли импульсов. Однако одного фильтра «я буду торговать в такие дни» недостаточно, чтобы разбить центр распределения. Это не магическая кнопка. Чтобы фильтр работал, он должен менять форму распределения, а не просто соответствовать нашим ожиданиям.

ПС
Думаю, теперь вам стало понятнее, как именно я подхожу к анализу методов, которые использую для подбора фильтров входа в позицию: я сравниваю, как они влияют на форму распределения, и сразу вижу, насколько выбранный мною фильтр - это не просто попытка выдать желаемое за действительное, а статистически обоснованный инструмент.

Ого, впечатлило...
Текст не ИИ? )))

 

[сибиряк-патр.]

я так и не понял что торгуем и какую кнопку жать покупать аль продавать?

 

[Olchik]

Ого, впечатлило...
Текст не ИИ? )))

А вот попробуйте дать ИИ задание написать текст на тему рыночных распределений, и он вам выдаст шаблонный обзор с определениями, ссылками на модели и аккуратными формулировками. ИИ не имеет личного опыта, чтобы понимать, что хвостовые события - это не книжная идея, а то, на чем может строиться стратегия, так как он никогда не попадал в хвост распределения сам, не пытался его поймать, не строил фильтры, в принципе не пытался отделить шум от сигнала. ИИ никогда не полезет в источники, не скачает историю котировок, не разобьет ее на выборки, чтобы сравнить формы распределений с фильтрами и без. Ему все равно, ведь он не торгует, не рискует, и не ошибается. Нейросеть не выдает тексты, содержащие уникальные мысли и теории, наоборот, она выдает то, что чаще всего встречалось в обучающих выборках: усредненные формулировки, типовые подходы, популярные теории. Да, ее текст может выглядеть аккуратно, грамотно, так же, как и текст грамотного и образованного человека.
Ну и так, на всякий случай, результат детектора в прикреплении.

 

[Olchik]

я так и не понял что торгуем и какую кнопку жать покупать аль продавать?

Я никуда не тороплюсь, ведь жизнь кончается не завтра. (С) Будет время и будет практика.
А пока хочу объяснить, почему моя концепция слабо коррелирует с большинством популярных в сети версий опционного анализа.

Если кому-то скучно, загляните через недельку. Примерно тогда начну разбирать конкретные кейсы, и, возможно, станет чуть интереснее.

 

[Sergerk]

А вот попробуйте дать ИИ задание написать текст на тему рыночных распределений, и он вам выдаст шаблонный обзор с определениями, ссылками на модели и аккуратными формулировками. ИИ не имеет личного опыта, чтобы понимать, что хвостовые события - это не книжная идея, а то, на чем может строиться стратегия, так как он никогда не попадал в хвост распределения сам, не пытался его поймать, не строил фильтры, в принципе не пытался отделить шум от сигнала. ИИ никогда не полезет в источники, не скачает историю котировок, не разобьет ее на выборки, чтобы сравнить формы распределений с фильтрами и без. Ему все равно, ведь он не торгует, не рискует, и не ошибается. Нейросеть не выдает тексты, содержащие уникальные мысли и теории, наоборот, она выдает то, что чаще всего встречалось в обучающих выборках: усредненные формулировки, типовые подходы, популярные теории. Да, ее текст может выглядеть аккуратно, грамотно, так же, как и текст грамотного и образованного человека.
Ну и так, на всякий случай, результат детектора в прикреплении.

Не, не хотел обидеть... ))
Я так понял, что имеются в виду графики - это типа распределение Гаусса и Гаусс с "тяжелыми" хвостами?

 

[Olchik]

Я так понял, что имеются в виду графики - это типа распределение Гаусса и Гаусс с "тяжелыми" хвостами?

Гаусса с тяжелыми хвостами не бывает, это противоречит самой природе нормального распределения. Я как раз об этом писала в первом сообщении на этой странице. Реальное рыночное распределение отличается от нормального тем, что у него более выраженный пик в центре и утолщенные хвосты. То есть это не «Гаусс с хвостами», а скорее эмпирическое распределение, которое можно сравнить с нормальным, чтобы показать, насколько рынок отклоняется от теоретической модели. Такое сравнение необходимо в ряде случаев, особенно если кто-то начинает изучать ценообразование опционов и не понимает, почему улыбка волатильности «улыбается». Но кроме того, настоящая форма рыночного распределения не учитывает реальные риски в хвостах. В принципе, об этом я тоже писала ранее.

 

[Sergerk]

Гаусса с тяжелыми хвостами не бывает, это противоречит самой природе нормального распределения. Я как раз об этом писала в первом сообщении на этой странице. Реальное рыночное распределение отличается от нормального тем, что у него более выраженный пик в центре и утолщенные хвосты. То есть это не «Гаусс с хвостами», а скорее эмпирическое распределение, которое можно сравнить с нормальным, чтобы показать, насколько рынок отклоняется от теоретической модели. Такое сравнение необходимо в ряде случаев, особенно если кто-то начинает изучать ценообразование опционов и не понимает, почему улыбка волатильности «улыбается». Но кроме того, настоящая форма рыночного распределения не учитывает реальные риски в хвостах. В принципе, об этом я тоже писала ранее.

Да, знаю - просто так обычно говорят... )))
Имхо, это не самый подходящий инструмент, чтобы поковырять рынок... ))
Как-то у меня возник к нему вопрос, но было не до него, и я так его и не порешал.
А вопрос в том, что такого рода распределение совершенно равнодушно к последовательности появления этих самых приращений...
Согласитесь, что, даже имея приращения, полностью укладывающиеся в Гаусса, если эти приращения выстроены так, что, например, сначала все с плюсом, а, затем, все с минусом, то мы получим хорошие такие тренды - сначала вверх, а потом - вниз... )

 

[Billy Kid]

Завтра евреи снова по Катару бомбанут и начнется весело на газовом рынке

 

[Olchik]

Согласитесь, что, даже имея приращения, полностью укладывающиеся в Гаусса, если эти приращения выстроены так, что, например, сначала все с плюсом, а, затем, все с минусом, то мы получим хорошие такие тренды - сначала вверх, а потом - вниз... )

Мой подход немного другой: я анализирую, как фильтры (например, дни выхода NFP) влияют на форму распределения доходностей. То есть сравниваю, насколько фильтр смещает массу наблюдений от центра к хвостам и как это отражается на вероятности импульсных движений. Это скорее статистический срез, чем динамический. Вы говорите о том, что даже при «нормальных» приращениях можно получить тренд, если они выстроены в определенной последовательности. А я о том, как фильтр может изменить саму форму распределения, чтобы повысить вероятность появления таких приращений.

По сути, ваша мысль касается закономерностей в последовательности, а моя в частотности. И, по-хорошему, эти подходы стоит объединять: фильтр, который меняет форму распределения, должен (или, по крайней мере, может) менять и структуру последовательности. Если я правильно поняла вашу мысль, то мы просто смотрим на один и тот же процесс с разных сторон

Завтра евреи снова по Катару бомбанут и начнется весело на газовом рынке

Это интересно, но пока нет времени следить за рынком. Небольшая запарка по работе, думаю, разгребусь ближе к началу или даже середине следующей недели.

 

[Olchik]

Опционный анализ: как перестать читать сказки​

Если вы когда-либо зададитесь вопросом разобраться в теме опционного анализа, то сразу же наткнетесь на форумные посты с тезисами вроде:

• куда ждет (или куда не ждет) цену маркетмейкер;
• на каких уровнях покупатели контрактов начнут получать прибыль, а значит, за какие пределы маркетмейкеру невыгодно выпускать рынок;
• где покупатели получат максимальные убытки (max pain) и куда погонит цену маркетмейкер;
• как открытый интерес по CALL и PUT формирует границы рынка;
• или не дай бог что-нибудь про уровни комфорта клиринговой палаты

Сразу обрадую, что эти идеи - плод фантазий псевдоэкспертов, которые не удосужились вникнуть в нюансы ценообразования рынка опционов, не открыли ни одной серьезной книги по данной теме и даже не знают, кто такой маркетмейкер, какие риск-модели он применяет и на чем вообще зарабатывает. Между прочим, это тема для отдельного ликбеза, страниц на пять, не меньше. Как-нибудь потом, может быть.

Все эти «аналитические» конструкции, щедро раскиданные по форумам, не просто ошибочны, они абсурдны. Примерно на том же уровне, как если бы сегодня всерьез утверждать, что Земля стоит на трех китах. Поэтому, если после попытки впитать такие «знания» вы решили, что опционы - это шаманство для узкого круга фанатиков, то вы просто читали не тех и не там. Давайте я подскажу, с чего начать, если вы хотите понять, как все устроено на самом деле.

Что стоит читать​

Мое предложение состоит в том, чтобы читать мнение профессионалов, то есть тех, кто работает в индустрии, торгует опционами на профессиональном уровне, строит собственные риск-модели, отлично ориентируется в инфраструктуре опционного рынка, понимает роли и функции его ключевых участников, занимается исследованиями и способен формулировать объективные, подкрепленные практикой и расчетами теории и выводы. Да, далеко не все из них охотно делятся своими наработками в открытом доступе, но кое-что найти все же можно.

Один из первых достойных материалов, который попался мне на эту тему в поиске - цикл статей Exchange Traded Options Market Making, Explained от Rohan Reddy. Это директор по исследованиям в Global X ETFs, крупной инвестиционной компании, специализирующейся на биржевых фондах. Статьи опубликованы на официальном сайте Global X ETFs, в которых достаточно подробно разбирается:

• роль маркетмейкеров в экосистеме биржевых опционов;
• реальные метрики, которыми они оперируют (включая такие параметры как дельта, гамма, тета и пр.);
• логика управления опционного портфеля через хеджирование, обоснованного необходимостью нейтрализации риска не только по дельте, но и по гамме;
• и в целом почему маркетмейкеру не важно, куда «пойдет цена», а важно только то, как быстро и эффективно он сможет нейтрализовать риск.

Это и есть настоящая кухня опционного рынка. В принципе, этот цикл статей одновременно и критикует, и подтверждает концепцию, которую я хочу проверить. Мне импонирует такой подход - когда идея рассматривается с разных сторон, без попытки выдать ее за истину в последней инстанции. Я давно в трейдинге и уже привыкла к тому, что ничего идеального нет. Но это не проблема, если есть понимание, что вероятности - это не про 100%, а иногда даже про какие-нибудь 55,5%. Главное осознавать, что рынок не обязан вести себя «логично» всегда, и что задача трейдера работать с допусками, сценариями и управляемым риском.

 

[сибиряк-патр.]

да когда уже кнопку то жать а главное покупать аль продавать

 

[Viktor-M]

вы знаете об особенностях дельта-хеджирования опционов

Я вообще игнорирую в своей торговле любые опционные стратегии . Они мешают точному входу . Я торгую одиночными сделками и не усредняюсь. Так что с хеджерами мы друг друга вряд ли поймем . Совсем другое дело в случае с роботами и ИИ , возможно я и включу когда то этот вид анализа для своего будущего большого робота , если тесты покажут что то интересное.
.

 

[Olchik]

Я вообще игнорирую в своей торговле любые опционные стратегии .

Ок, но стоит уточнить, что под «опционными стратегиями» в нашем разговоре имеются в виду не классические конструкции вроде «стрэддла» или «спрэда», а торговые подходы на базовом активе (например, на золоте), основанные на анализе данных с опционного рынка. Уточнение, чтобы не возникала путаница, ведь опционные стратегии - это еще и то, как торгуют трейдеры опционов.

Я торгую одиночными сделками и не усредняюсь.

Я тоже торгую одиночными сделками и не усредняюсь.

Совсем другое дело в случае с роботами и ИИ , возможно я и включу когда то этот вид анализа для своего будущего большого робота , если тесты покажут что то интересное.

Для начала вам предстоит найти действительно интересный материал по этой теме. И тут вам, можно сказать, повезло: то, что я здесь пишу, вы вряд ли встретите где-то еще. По крайней мере, я не видела. Все, что мне попадалось до сих пор по теме опционного анализа - это откровенная муть от людей, которые вообще не понимают, как устроен рынок опционов. Я сама неплохо ориентируюсь в этой теме, конечно, я не углублялась до уровня квантовых моделей, ))) но имею хорошую базовую теоретическую подготовку, которая позволяет отличать дилетантские идеи от тех, что действительно заслуживают внимания. Если отделить зерна от плевел, то вариантов использования процессов, происходящих на опционном рынке, для прогнозирования движения базового актива, не так уж много. По сути, все сводится к эффекту от дельта-хеджирования. О нем как раз собираюсь рассказать в этой ветке. И это не только мое мнение, это мнение профессионалов, тех самых квантов из хедж-фондов. Я позже упомяну еще несколько достойных работ на эту тему. Хотя есть и обратная сторона, допустим, идея окажется состоятельной, но проверить ее на исторических данных будет непросто. Доступ к архивам CME платный, и цены там, мягко говоря, кусаются. Так что, скорее всего, придется обходиться без полноценного тестирования на истории.

 

[Olchik]

Один из первых достойных материалов, который попался мне на эту тему в поиске - цикл статей Exchange Traded Options Market Making, Explained от Rohan Reddy. Это директор по исследованиям в Global X ETFs, крупной инвестиционной компании, специализирующейся на биржевых фондах. Статьи опубликованы на официальном сайте Global X ETFs, в которых достаточно подробно разбирается:

Возвращаясь к статьям Рохана Редди, где он подробно объясняет, как устроен маркетмейкинг на рынке биржевых опционов.



В первой части первой статьи он упоминает, насколько вырос интерес к опционам после ковида, и это, действительно, впечатляет: объемы торгов удвоились, а индексные опционы на S&P 500 и Nasdaq 100 показали рекордные значения открытого интереса.

Но нас интересует как маркетмейкер управляет своими опционными портфелями. Хотя я вроде как обещала не углубляться в ликбез (иначе это займет страниц пять, не меньше), но раз уж сам Редди затронул этот вопрос, позволю себе сделать на нем небольшой акцент.

Ближе к середине статьи Редди формулирует три основные роли маркетмейкера:

• обеспечивает ликвидность, то есть у него есть обязанность покупать и продавать активы в любой момент, чтобы инвесторы могли быстро и легко входить и выходить с рынка по справедливой цене;
• поддерживает порядок и эффективность, предоставляя двухсторонние котировок (bid/ask), тем самым предотвращая резкие ценовые колебания;
• содействует прозрачности биржевого ценообразования, то есть он публично раскрывает свои котировки, чтобы инвесторы могли видеть реальные цены и принимать обоснованные решения.

И вот здесь начинается самое интересное. В обязанности маркетмейкера входит держать двустороннюю котировку. Причем это не просто пожелание, а формальное требование, прописанное в регламенте биржи. Я хочу заострить внимание именно на этом моменте, потому что он напрямую противоречит популярной теории заговора, согласно которой маркетмейкер - это такой «кукловод», двигающий цену туда, куда ему выгодно, оставляя толпу с убытками. Если вдуматься, обязанность одновременно покупать и продавать уже ограничивает его свободу «возить цену по графику». А если добавить к этому еще и юридическую ответственность за манипуляции вплоть до уголовной, то образ всесильного кукловода начинает трещать по швам.

Дальше в статье обсуждаются несколько специфических терминов из мира опционов, и вот тут я не уверена, стоит ли грузить ими непосвященную публику. Могу поделиться своим опытом: когда я начала изучать опционы, все казалось невероятно сложным, как будто это какая-то поствысшая математика, которую я не осилю никогда. Опционы совсем не похожи на торговлю базовым активом, даже близко. Но, к моему удивлению, я освоила их довольно быстро. А потом, общаясь на форумах, я видела, как люди годами не могут понять даже самые азы. Я снова подумала о своем опыте и сделала такой вывод, что несмотря на мою въедливость и склонность копать до последней жилки, когда на меня обрушился этот пласт неподъемной (как казалось в тот момент) теории, я сказала себе: «Окей, я сейчас это не понимаю. Просто запомню, что это так, и пойду дальше. А потом, с опытом, пойму, почему это так». Наверное, именно это и помогло мне относительно быстро освоить тему опционов.

Почему я сейчас вспомнила об этом? Просто потому, что предлагаю вам поступить ровно так же. Если вы хотите вникнуть в опционный анализ, но не планируете торговать опционами, то лучше просто запомнить некоторые вещи. В опционах есть свои очень специфические понятия, которые никак не коррелируют с тем, как устроена торговля базовым активом (тем же фьючерсом). И первая вещь, которую нужно запомнить, это то, что маркетмейкер занимает рыночно-нейтральную позицию. Он делает все возможное, чтобы не оказаться в направленной позиции, другими словами, чтобы не зарабатывать на росте базового актива и не терять на падении. Это называется устранить рыночный риск. Для этого он применяет в том числе так называемое дельта-хеджирование.

В рамках дельта-хеджирования маркетмейкер вынужден покупать или продавать базовый актив. То есть, если он продает опционы на фьючерс золота, то, чтобы исключить рыночный риск, он будет продавать или покупать фьючерс на золото, причем делать он это будет строго по системе дельта-хеджирования. И это и есть единственное, что на самом деле связывает работу маркетмейкера на рынке опционов с динамикой самого фьючерса. Больше ничего не связывает. Поэтому если эта связь не работает, и в ней не получится найти закономерности, то и на теме опционного анализа можно ставить жирный крест. Вот такие мысли у меня на этот счет. Подробности позже.

 

[dobi82]

Возвращаясь к статьям Рохана Редди, где он подробно объясняет, как устроен маркетмейкинг на рынке биржевых опционов.

Посмотреть вложение 575238

В первой части первой статьи он упоминает, насколько вырос интерес к опционам после ковида, и это, действительно, впечатляет: объемы торгов удвоились, а индексные опционы на S&P 500 и Nasdaq 100 показали рекордные значения открытого интереса.

Но нас интересует как маркетмейкер управляет своими опционными портфелями. Хотя я вроде как обещала не углубляться в ликбез (иначе это займет страниц пять, не меньше), но раз уж сам Редди затронул этот вопрос, позволю себе сделать на нем небольшой акцент.

Ближе к середине статьи Редди формулирует три основные роли маркетмейкера:

• обеспечивает ликвидность, то есть у него есть обязанность покупать и продавать активы в любой момент, чтобы инвесторы могли быстро и легко входить и выходить с рынка по справедливой цене;
• поддерживает порядок и эффективность, предоставляя двухсторонние котировок (bid/ask), тем самым предотвращая резкие ценовые колебания;
• содействует прозрачности биржевого ценообразования, то есть он публично раскрывает свои котировки, чтобы инвесторы могли видеть реальные цены и принимать обоснованные решения.

И вот здесь начинается самое интересное. В обязанности маркетмейкера входит держать двустороннюю котировку. Причем это не просто пожелание, а формальное требование, прописанное в регламенте биржи. Я хочу заострить внимание именно на этом моменте, потому что он напрямую противоречит популярной теории заговора, согласно которой маркетмейкер - это такой «кукловод», двигающий цену туда, куда ему выгодно, оставляя толпу с убытками. Если вдуматься, обязанность одновременно покупать и продавать уже ограничивает его свободу «возить цену по графику». А если добавить к этому еще и юридическую ответственность за манипуляции вплоть до уголовной, то образ всесильного кукловода начинает трещать по швам.

Дальше в статье обсуждаются несколько специфических терминов из мира опционов, и вот тут я не уверена, стоит ли грузить ими непосвященную публику. Могу поделиться своим опытом: когда я начала изучать опционы, все казалось невероятно сложным, как будто это какая-то поствысшая математика, которую я не осилю никогда. Опционы совсем не похожи на торговлю базовым активом, даже близко. Но, к моему удивлению, я освоила их довольно быстро. А потом, общаясь на форумах, я видела, как люди годами не могут понять даже самые азы. Я снова подумала о своем опыте и сделала такой вывод, что несмотря на мою въедливость и склонность копать до последней жилки, когда на меня обрушился этот пласт неподъемной (как казалось в тот момент) теории, я сказала себе: «Окей, я сейчас это не понимаю. Просто запомню, что это так, и пойду дальше. А потом, с опытом, пойму, почему это так». Наверное, именно это и помогло мне относительно быстро освоить тему опционов.

Почему я сейчас вспомнила об этом? Просто потому, что предлагаю вам поступить ровно так же. Если вы хотите вникнуть в опционный анализ, но не планируете торговать опционами, то лучше просто запомнить некоторые вещи. В опционах есть свои очень специфические понятия, которые никак не коррелируют с тем, как устроена торговля базовым активом (тем же фьючерсом). И первая вещь, которую нужно запомнить, это то, что маркетмейкер занимает рыночно-нейтральную позицию. Он делает все возможное, чтобы не оказаться в направленной позиции, другими словами, чтобы не зарабатывать на росте базового актива и не терять на падении. Это называется устранить рыночный риск. Для этого он применяет в том числе так называемое дельта-хеджирование.

В рамках дельта-хеджирования маркетмейкер вынужден покупать или продавать базовый актив. То есть, если он продает опционы на фьючерс золота, то, чтобы исключить рыночный риск, он будет продавать или покупать фьючерс на золото, причем делать он это будет строго по системе дельта-хеджирования. И это и есть единственное, что на самом деле связывает работу маркетмейкера на рынке опционов с динамикой самого фьючерса. Больше ничего не связывает. Поэтому если эта связь не работает, и в ней не получится найти закономерности, то и на теме опционного анализа можно ставить жирный крест. Вот такие мысли у меня на этот счет. Подробности позже.

Может просто расскажешь о своей системе в кратце, когда покупать а когда продавать?

 

[Olchik]

Может просто расскажешь о своей системе в кратце, когда покупать а когда продавать?

Нет, не продолжу. Я буду двигаться в том русле, в котором я хочу двигаться. А если кого-то что-то не устраивает, вы можете не читать, никто же вас сюда насильно не тащит, верно? Это мой дневник и я сама решаю, что здесь писать. Рада, что мое творчество вызывает у некоторых такое обострение. )))

 

[Olchik]

Гамма-сквиз​

Подытожу немного. Как я уже писала выше, маркетмейкер обязан поддерживать двустороннюю котировку, то есть быть готовым как купить, так и продать опцион в любой момент. Его доход формируется в основном за счет спреда между ценой покупки и продажи. Поэтому он стремится сохранять рыночную нейтральность через хеджирование проданных и купленных опционов сделками на базовом активе по особой системе «дельта-хеджирования». Если, допустим, маркетмейкер не станет хеджировать свои позиции, то при росте рынка он окажется в чистом шорте, а при падении - в чистом лонге, и останется банкротом, так как спред и опционные премии несоизмеримо малы с теми, какие изменения стоимости может продемонстрировать базовый актив.

То есть дельта-хеджирование дает возможность маркетмейкеру уйти от рыночного риска. Но в определенные моменты оно же может привести к обратному эффекту, так называемому гамма-сквизу. Например, при быстром росте рынка инвесторы массово покупают колл-опционы (ставка на рост цены актива). Когда цена актива приближается к страйку опциона, дельта (чувствительность опциона к цене актива) и гамма (чувствительность дельты к цене) резко растут. Маркет-мейкер, продавший коллы, вынужден активно скупать базовый актив для хеджирования, что само по себе разгоняет цену, создавая цепную реакцию. Это и есть та самая связь, которую имеет смысл проверить.

Существует несколько исторических примеров, когда гамма-сквиз приводил к серьезному ралли на рынке акций. О них вы можете прочесть в интернете, например, случай с акциями AMC в 2021 году:

источник: reuters.com/business/what-is-gamma-squeeze-how-did-it-drive-up-amcs-stock-price-2021-06-03/

Понятно, что акции не настолько ликвидны, как, скажем, то же золото, поэтому таких уж значительных всплесков на товарных активах вряд ли стоит ожидать, тем более ситуации не будут возникать постоянно. Это редкие случаи. Но тем не менее понаблюдать стоит.

 

[Olchik]

На следующей неделе планирую присмотреться к отчетам на сайте CME и начать изучать функционал QuikStrike. Честно говоря, пока знакома с ним весьма поверхностно, так как раньше не использовала в торговле никакие техники так называемого опционного анализа, так как не находила в сети ничего действительно вменяемого на эту тему. Эту тему часто обсуждают трейдеры, которые сами в опционах по нулям, как и в биржевом трейдинге, но зато отлично ориентируются в QuikStrike. У меня же наоборот: в опционах разбираюсь на вполне нормальном уровне, а вот с QuikStrike пока на вы.

Начну с фьючерса на золото (GOLD), буду отслеживать динамику открытого интереса. В частности, мне важно увидеть два обстоятельства:

• на каком-то страйке, куда цена еще не вырастала, скопился непривычно большой открытый интерес по коллам;
• рынок движется к этому страйку импульсно, то есть не вяло, не через откаты, а бодро и уверенно.
  

Последнее важно, потому что для эффекта, похожего на гамма-сквиз, нужно, чтобы гамма (один из опционных греков) росла агрессивно. Вдаваться в теорию не буду, ибо обязательно выскочат какие-нибудь умники и начнут рассказывать, что мне писать в моем дневнике.

Но чтобы вы уловили общую идею, «большой открытый интерес» - понятие относительное. Думаю, его нужно сравнивать с интересом на ближайших круглых страйках. И он должен явно выделяться. Например, сейчас я вижу на страйке 3500 открытый интерес более 20 000 коллов:




Если посмотреть на чарт золота, видно, что цена пролетела в свое время этот участок импульсом:



Сейчас на страйке 3800 скопился приличный открытый интерес, более 22 000 контрактов по коллам:



Страйк 3800 - это скорее зона, чем конкретный уровень, поскольку контракты с разными сроками истечения отличаются по цене: чем дальше фьючерс, тем он дороже. Поэтому ориентироваться нужно не на точку, а на диапазон. Когда цена подойдет к этой зоне, особенно если к тому моменту вырастет открытый интерес по коллам, планирую пробовать заходить в лонг с расчетом на импульсное движение. Такой у меня план.

Пока осваиваю QuikStrike, но как только сориентируюсь в его функционале, возьму на прицел другие активы и начну собирать статистику. Хочу выстроить системный подход, основанный на наблюдении за динамикой открытого интереса и реакцией рынка на ключевые страйки. Надеюсь, не сильно умно написала, никого не бомбанет. Старалась написать попроще, но просто сразу потупеть не могу, извините. Может, со временем, но это неточно.

Всем хорошего настроения!